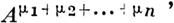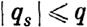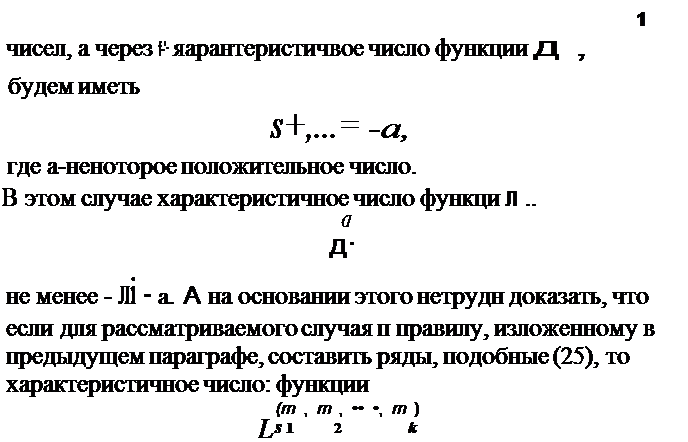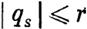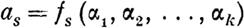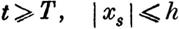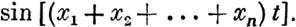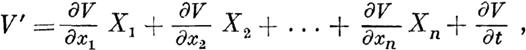Рнь>: У. 6 страница

ОБЩАЯ 3АДАЧА ОБ УСТОЙЧИВОСТИ движвния

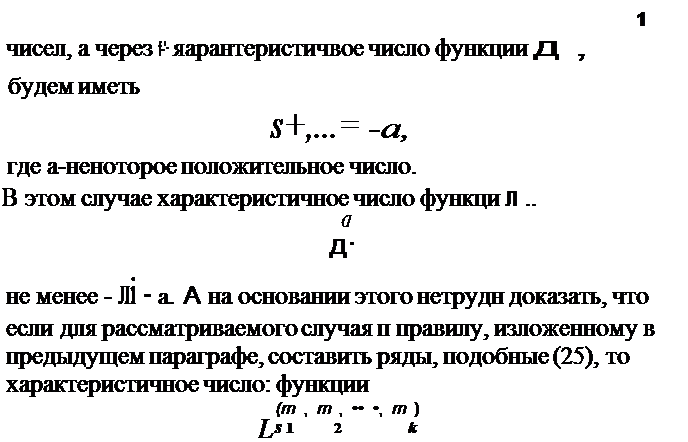будет не менее - ( т₁+ т₂-1- . • + т k - 1) а. Допустим, что а менее каждого из чисел л1, Л2, ... ' лk. Тогда надлежащим выбором чисел s и "'i можно будет удовлетворить всем неравенствам s +а k) ~'S > 8 > "fl > ₂ (s = 1, 2, ... , • А при выполнении последних будут выполнены все условия предыдущего доказатсльетва, в чем легко убедимся, принимая в расчет только что указанное свойство функций L. Поэтому теорема будет справедлива и в случае, когда система дифференциальных уравнений первого приближения не есть правильная, но каждое из харакрврисгичвых чисел, взятых для составления рядов (25)t олее а, - если только условие з > () заменим в ней словием з > а. 13. Вытекающие из теоремы о сходимости заключения об устойчивости.Из цокаванного могут быть выведены следующие теоремы: Те о рем а 1. Если система дифферен,циальиых равнений первого приближения есть правильная и если

А. М. ЛЛПУНОВ

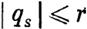
ОБЩАЯ 8АдАЧА ОБ УСТОЙЧИВОСТИ ДВИЖЕНИЯ 7~,

довлетворяющих условиям 1 а, 1 < а ( s == 1, 2, ... , п), (36) модули величин as, определяемых уравнениями (35), не будут превосходить величины r. Тогда можем быть уверены, что если начальные обстоятельства возмущенного движения выбраны согласно условиям: (36), то в течение всего последующего времени движения будут выполняться уеловия: lxs/ < х, (s== 1, 2, ... , п), а этим и доказывается теорема. Примечание. При условиях предыдущей теоремы во веяном возмущенном движении, достаточно близком :к_ невозмущенному, все функции », с беспредельным возрастанием t стремя гся .к нулю. Это обстоятельство мы будем выражать, говоря, что воэмищенное движение (поскольку оно определяется выражениями величин xs в функциях t) асимптотически приближается К, невовмущен,н,о.му. Далее мы будем часто говорить также о движениях, асимптотически приближающихся н какому-либо данному движению. После замеченного сейчас, аначенио такого выражения не требует особых разъяснений. Т е о р е м а 11. Если система дифференциальных уравнений первого приближения есть правильная, а в группе ее хар актеристичных чисел находятся положительные, то невоэмцщенное движение всегда обладает. игесстною ус,~овно;о устойчивистыо. А именно, если число положительных характеристичных 'Чисел есть k, то для устойчивости достаточно, 'Чтобы начальные значения а₁, а₂, ••• , ап неизвестных фун-к,ций иддвлетворяян некоторым n-k уравнениям вида Fi(a₁, а₂, ••• ,ап)=О (j==1, 2, ... ,n-/r,), где F₁суть голоморфные фун,К,цuи величин а₈, упи - чтожающиеся при а₁= а₂== ••• = ап == О. У'равнения дmи mаК,овы, что поаволя ,от вы ража,пи ссе as 1ra1~

х-:-м. лнптпов

всщестеенные голоморфные функции некоторых k вещественных независимых величин. Будем предполагать все функции, входящие в состав нормальной системы решений уравнений (6), которою мы пользовались для составления рядов (25), вещественными. Тогда вычисления можно вести так, что все коэффициенты L в уравнениях (25) также будут вещественными, и, следовательно, уравнения:ми этими при вещественных ai будет определяться некоторое вещественное решение системы уравнений (1). Допуская это и делая в уравнениях (25) t =0, найдем: (s = 1, 2, ... , п), где fs суть вещественные голоморфные функции величин ai, обращающиеся в нуль, когда все a.j полагаются равными нулю. Притом функции эти таковы, что между фуннциональвыми определителями, которые можно из них составить, комбинируя их по k, найдется по крайней мере один, который не будет обращаться в нуль, когда сделаем

ибо при этом определители эти обращаются в значения, соответствующие t = О, миноров определителя д, составленных из элементов его первых k строк. Вследствие этого из предыдущих уравнений при достаточно малых ! а₈1 можем вывести следующие:

а j == 'Pi ( а1' а2, ... ' ап) F s ( а₁, а₂, ••• , a,J === О

(j == 1, 2, ......... , k), (s== 1, 2, , n-k), (37)

где Ч>i, Fs суть нкоторые голоморфные функции вели- чин а₁,а₂, •• , а₁" обращающиеся n нуль, когда пос- ледние все делаются равными нулю. Дальнейrпий ход докааательства будет тот же, что и для предыдущей теоремы, с тою только разницей, что здесь мы должны иметъ в виду п - k уравнений (37), связываюших величины а ...

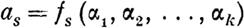
ОБЩАЯ ?АДАЧА ОБ УСТОИЧИВОСТИ ДВИЖЕНИЯ 7?

~~г.-ляп УН о в

На основании изложенного мы можем утверждать, что такие функции по крайней мере для значений t, достаточно близких :н t₀, всегда найдутся и выйдут вещественными веяний раа, когда такими выбраны все а₅(это мы и будем здесь првлполагатъ), и что притом всегда найдется такой предел t₁, больший t₀, чтобы в промежутке от t₀до t₁включительно функции эти представлялись рядами, расположенными по целым: положительным степеням постоянных а₅• Если определяемые этими рядами функции при t ==l₁удовлетворяют неравенствам 1Х₈1 < А (s == 1, 2, ... , п), (38) то для них навечно возможвы будут аналитические продолжения и за предел t₁, представляемые подобными же рядами, расположенными по степеням значений этих функций для t == tl. Эти новые выражения функций Х₈вообще будут справедливы только для значений t, не превосходящих некоторого предела t₂• Но если при t ==t₂неравенства (38) остаются выполненными, для наших функций будет возможно дальнейшее продолжение под видом пекоторых новых рядов такого же харакгера. 'Гвним образом, исходя из данных начальных значений а₈, можно будет следить за непрерывным изменением наших функций при непрерывном возрастании t u u по краинеи мере до тех пор, пока не нарушаются неравенства (38). Может случиться, что при каном-либо выборе постоянных as неравенства эти будут выполняться для всех значений t, больших t₀• Тогда функции xs определятся для: всех таких значений t. В других случаях для t будет существовать неноторый высший предел t', при котором по крайней мере одно из неравенств (38) перейдет в равенство. Аналитическое продолжение наших фуннций за такой предел t' потребовало бы, навечно, особого исследования. Но нам входить в него не представится надобности, таи нан для нашей цели будет достаточно рас-

ОБЩАН 2АДАЧА ОБ УСТОЙЧИВОСТИ ДВИ!ЬЕНИЯ

сматривать веяное возмущенное движение только до тех пор, пона величины \ Х₈\ не превосходят какихлибо данпых отличных от нуля пределов. Во веяном случае постоянные а₈всегда можно будет выбрать настолько численно малыми, чтобы наши аналитические выражения функций Х₅годились для всех значений t, лежащих между t₀и Т, как бы велико ни было данное число Т, и чтобы значения "",. 1- ф u Тб ~,, ~₂, ••• , ~п этих уннции для t = ыли все CEOJIЬ угодно численно малыми, Притом, если бы мы пожелали определять функции xs их аначенипми es для t === Т, то как бы велико ни было Т, все ts всегда можно было бы выбрать настолько численно малыми, чтобы этим значениям соответствовала одна определенная система начальных значений а₈и чтобы последние были все сколь угодно численно малыми, Из этого последнего замечания следует, что при решении вопросов об устойчивости достаточно будет рассматривать только значения t, большие сколь угодно большого предела Т, изаменять рассмотрение начальных значений функций Х₈рассмотрением их значений, соответствующих t == Т. Мы будем далее рассуждать о функциях Х₈только но тех пор, пока не нарушаются неравенства (38). Поэтому, говоря о каних-либо пределах для величин! х₅1, эти пределы всегда будем предполагать меньшими А. 15. Некоторые определения.Мы будем здесь рассматривать вещественные функпии вещественных переменных (39)

подчиненных некоторым условиям вида t>T,

(40)

где Т и Н суть постоянные, из которых вторая всегда будет предполагаться отличною от нуля. Притом мы будем рассуждать только о функциях, которые при условиях (40) остаются непрерывными

А.

япгно

и однозначными и уничтожаются при Х ₁= Х₂= . . . === Х п = 0. Такими свойствами будут обладать все рассматри ваемые нами функции (хотя бы об этом и не было упо мянуто). Но кроме того они могут обладать более спе циальными свойствами, для обозначения которых мы введем некоторые термины. Пусть рассматривается фуннция V, которая такова, что при условиях (40), если в них Т сделать достаточно большим, а Н достаточно малым, она может получать, кроме равных нулю; только значения одного каноголибо звана. 'Гакую функцию будем называть энакопостоянною . Когда же пожелаем указатъ на ее знак, то будем говорить, что это есть функция положительная или отрицательная. Притом, если функция V не зависит от t, а постоянная Н может быть выбрана достаточно малой для того, чтобы при условиях (40) равенство V == О могло иметь место только для одной системы значений переменных Х₁= Х₂= ... = Хп == 0, то функцию V будем называть энакоопредеяенною, а жешая обратить внимание на ее зван - определенно-положительною или определенно-отрицательною. Последними терминами мы будем пользоваться также и по отношению н функциям, зависящим от t. Но в этом случае функцию V будем называть знакоопрееленною только при условии, если для нее возможно айти такую независящую от t определенно-положи- ельную функцию iv, при которой одно из двух выраений V-W или -V-W редставляло бы функцию положительную [⁸]. Тан :каждая из фуннций х:- х:- 2х₁х₂cos t, t (х~ + х:) -- 2х₁х₂сов t

ОБЩАЯ ЗАДАЧА ОБ УСТОПЧИВОСТИ ДВИЖЕНИЯ

стъ анакопостоянная. Но первая есть только внако остоянная, а вторая, если п = 2, есть в то же время знаноопределенная. Веяную функцию V, для которой постоянная Н ожег быть выбрана настолько малой, чтобы для чис овых значений этой функции при условиях (40) суествовал некоторый высший предел, мы будем называть ограниченною. В силу свойств, ноторыми по нашему предполоению обладают все рассматриваемые нами функ- ии, такой будет, например, веяная не зависящая от ункция. Ограниченная функция может быть такова, что для сякого положительного z, как бы оно мало ни было, айдется такое отличное от нуля число h, при котором V ля всех значении переменных, удовлетворяющих ус- lловиям (s = 1, 2, ... , п), будет выполняться следующее: 1 V j<s.

Этому требованию удовлетворяет, например, веяная не зависящая от t функция. Но функции, зависящие от t, хотя бы и ограниченные, могут ему не удовлетво рятъ. Такой случай представляется, например, дл фуннции

:Когда для функции V предыдущее требование выполнено, мы будем говорить, что она допускает бесконечно малый высший предел. Такова, например, функция (х₁+ Х₂+ ... + хп) sin t. Пусть V есть фуннция, допускаюшея бесконечно малый высший предел. Тогда, если нам известно, что f\ А. М. Ляпунов

А.М~ЯПУНОВ

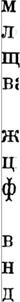
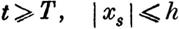
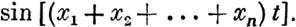
переменные удовлетворяют условиям

где l есть некоторое положительное число, то отсюда V заключим, что наидется некоторое другое положи- тельное число л., менее которого не может быть наибольшая из величин I х₁1, 1 х₂1, •.. , 1 хп \. Одновременно с функцией V мы будем часто рассматривать выражение

представляющее ее полную производную по t, взятую в предположении, что х₁, х₂, ••• , хп суть функции t, удовлетворяющие дифференциальным уравнениям возмущенного движения. В таних случаях всегда будем предполагать фуннцию V такой, чтобы V' как функция переменных (39) обладала всеми свойствами вообще рассматриваемых нами здесь функций. Говоря далее о производной функции V, будем u подразумевать, что речь идет о тольно что названнои V V полнои производнои. 16. Основные предяожения.Всем из.вестна теорема Лагранжа об устойчивости равновесия при существовании силовой фувкции и изящное доказательство, предложенное для нее Лежен-Дирихле ¹). Последнее основывается на соображениях, которые могут служить для цокааательства многих подобных теорем. Руководствуясь такими соображениями, мы донажем здесь следующие предложения: Т е о ре м а. Если диффере1-tциалъные у р аенения возмущенного движения таковы, 'Что возможно найти онакоопределеннцю фун,кцию V, проиеводная кото-

1) L аg r а n g е, Mecanique analytique, 3 или 4 ивд., том I, дополнение 11 [⁷].

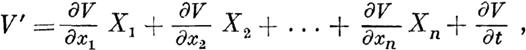
ОБЩ-Л:Я ЗАДАЧА ОБ УСТОЙЧИВОСТИ ДВИЖЕНИЯ

8Я

ой V' в силу этих уравнений была бы или внакопостоянною фу нкцией противоположного знака с V, ила тождественно р аеною нулю, то невогмищенное движенис стойчиво, Допустим, что найденная функция V определенноположительна, а производная ее V' представляет отрицательную функцию или тождественно равна нулю. Тогда найдутся такие постоянные Т и Н, при которых для всех значений переменных х ₁, х~, ... , хп, t, удовлетворяющих условиям: t > Т и

(s== 1, 2, ... ; п), будут выполняться следующие: V'<O, V>,W,

( 41)

(42)

выведем, что если в промежутке от Т до t условия (41 постоянно выполняются, то в том же промежутк функпии Х₅наверно будут удовлетворять условию , iv < V₀, (44) б*

Пусть l есть точный низший предел функции (как функции независимых переменных х₁, х₂, ••• , хп) при этом условии. Число l необходимо будет отличным от нуля и полоэкителъным, ибо функция W по своему характеру не может делаться при условии (45) ни отрицательною, ни равною нулю, а l в силу ее непрерывности необходимо будет одним из значений, которые она при этом условии может принимать. Поэтому всегда можно будет сделать vo < l,

V и притом всегда наидвтся такое отличное от нуля число л, при котором неравенство это будет выполняться для всяких ~s, удовлетворяющих условиям

(s== 1, 2, ... , п).

(46)

"У становив это, допустим, что величины es действительно выбраны согласно условиям ( 46). 'Ган как число л необходимо менее s, то функции Х₈будут тогда удовлетворять неравенствам

(s=1, 2, ... ,п)

(47)

ля всех достаточно блиаких н Т значений t. Но изменяясь с течением времени непрерывно, ункции xs не могут перестать удовлетворять этим 1еравенстваl\11 иначе, нан достигнув предварителт,но

⇐ Предыдущая 1 2 3 4 567 8 Следующая ⇒