Пример 10 7 страница

Глава 6. Уравнения равновесия

§ 6.1. Независимые уравнения равновесия для различных систем сил

Если твердое тело под действием некоторой системы сил находится в равновесии, то для этой системы сил главный вектор и главный момент, вычисленный относительно произвольной точки , равны нулю. Тогда из (69), (70) получим уравнения равновесия системы сил в векторной форме:

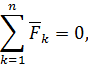
	(71)
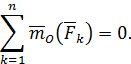
	(72)

Если векторные равенства (71), (72) записать в проекциях на выбранные оси координат, то из двух векторных уравнений получим 6 алгебраических уравнений равновесия:

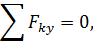
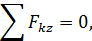
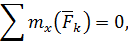
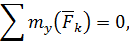
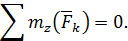
(73)

В формулах (73) суммирование производится для всех сил системы, но для краткости записи у знака суммы не указаны границы изменения индекса суммирования 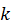. Будем использовать такое упрощение записи и в дальнейшем.

Отметим, что записанные выше уравнения равновесия (73) являются независимыми только для систем сил наиболее общего вида – пространственных произвольных. Для более простых систем сил независимых уравнений равновесия будет меньше шести. Ниже в таблице приведены независимые уравнения равновесия для систем сил различного вида. Эти независимые уравнения помечены в таблице знаком ( 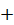). Отметим, что для плоских систем сил, расположенных в плоскости 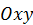, вычисление моментов сил относительно оси 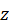эквивалентно вычислению алгебраических моментов сил относительно точки, выбранной в плоскости .

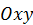Таблица 1. Независимые уравнения равновесия для различных систем сил

Уравнения равновесия	Вид системы сил
	Пространственная			Плоская (в плоскости )
	Произвольная	Параллельная	Сходящаяся	Произвольная	Параллельная	Сходящаяся

	+	–	+	+	–	+
	+	–	+	+	+	+
	+	+	+	–	–	–
	+	+	–	–	–	–
	+	+	–	–	–	–
	+	–	–	+	+	–
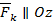
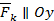
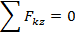
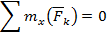
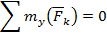
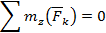
Количество независимых уравнений

Докажем одну важную теорему статики.

Теорема Вариньона

Если система сил имеет равнодействующую, то векторный момент равнодействующей силы относительно какого-либо центра равен геометрической сумме векторных моментов всех сил системы, вычисленных относительно того же центра.

Доказательство

Пусть на твердое тело действует система сил 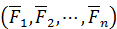, имеющая равнодействующую 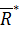(см. рис. 78) .

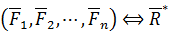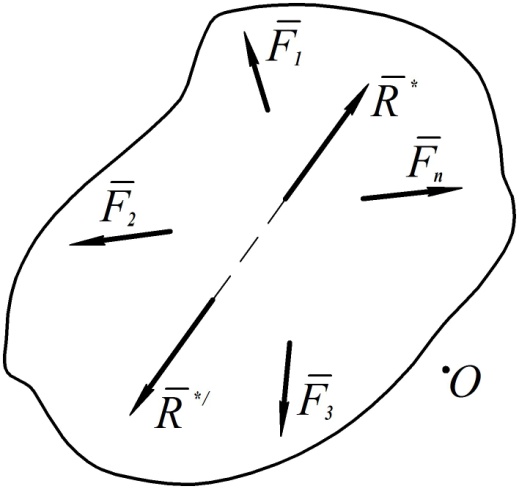Рис. 78

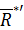Добавим к заданной системе сил уравновешивающую силу

, равную по величине, противоположно направленную и имеющую общую линию действия по отношению к равнодействующей силе

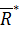. Тогда полученная система сил будет эквивалентна нулю

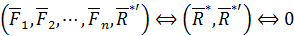
и должна удовлетворять уравнениям равновесия. В частности, сумма векторных моментов сил этой системы относительно любой точки равна нулю:

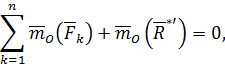
но

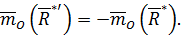
Тогда из предыдущей формулы получим

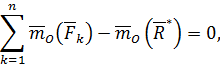
откуда следует утверждение теоремы:

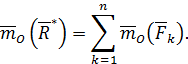
Отметим, что аналогичное утверждение справедливо для алгебраических моментов и моментов сил относительно осей.

§ 6.2. Различные формы независимых уравнений равновесия для плоской произвольной системы сил

В таблице 1 приведены независимые уравнения равновесия для плоской произвольной системы сил в виде

(74)

В третьем уравнении (74) моменты относительно оси заменены алгебраическими моментами относительно некоторой точки , лежащей в плоскости действия сил. Записанные уравнения (74) называют первой (или основной) формой независимых уравнений равновесия для плоской произвольной системы сил. При записи уравнений равновесия в этой форме оси координат и моментную точку можно выбирать произвольно в плоскости действия сил.

Покажем далее, что уравнения равновесия для плоской произвольной системы сил можно записывать еще в двух эквивалентных формах.

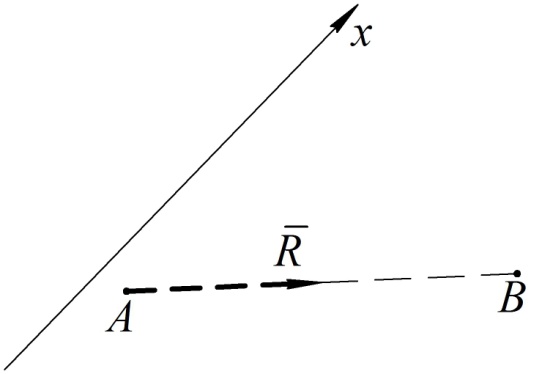Рис. 79

Допустим теперь, что равны нулю суммы алгебраических моментов всех сил системы относительно двух произвольных точек

и сумма проекций сил на ось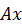

, не перпендикулярную

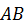(см. рис. 79):

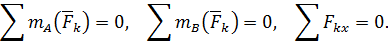
(75)

Докажем, что при выполнении уравнений (75) плоская система сил будет уравновешенной. Выберем в качестве центра приведения точку и покажем, что главный вектор системы сил и ее главный момент относительно точки равны нулю. В силу первого уравнения (75) главный момент относительно точки равен нулю:

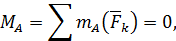
и рассматриваемая система сил эквивалентна равнодействующей 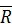, приложенной в точке . По теореме Вариньона и согласно второму уравнению (75)

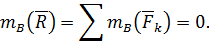
Следовательно, либо 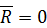, либо линия действия 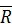проходит через точку . Допустим второе и обозначим равнодействующую штриховой линией на рис. 78. Тогда, как видно из рисунка,

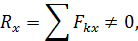
что противоречит третьему уравнению (75). Следовательно, 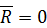и система сил является уравновешенной.

Уравнения (75) называют второй формой независимых уравнений равновесия для плоской произвольной системы сил. Здесь моментные точки и могут выбираться произвольно, а ось 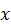, на которую вычисляются проекции сил в третьем уравнении, не должна быть перпендикулярна отрезку .

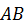Пусть теперь равны нулю суммы алгебраических моментов всех сил системы относительно трех точек , и , не лежащих на одной прямой:

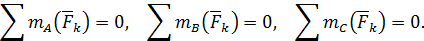
(76)

Докажем, что при выполнении уравнений (76) плоская система сил тоже будет уравновешенной. Выберем в качестве центра приведения точку и покажем, что главный вектор системы сил и ее главный момент относительно точки равны нулю. В силу первого уравнения (76) главный момент относительно точки равен нулю:

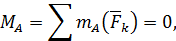
и рассматриваемая система сил эквивалентна равнодействующей 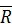, приложенной в точке . По теореме Вариньона и согласно второму уравнению (76)

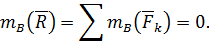
Следовательно, либо 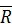=0, либо линия действия проходит через точку . Допустим второе и обозначим равнодействующую штриховой линией на рис. 80.

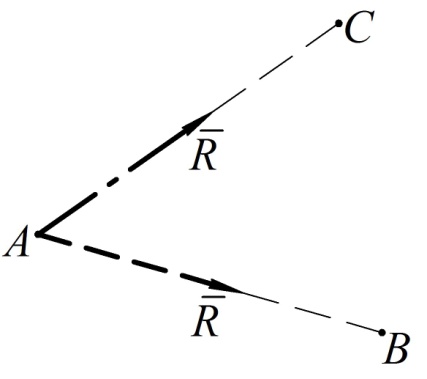Рис. 80

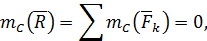
В силу теоремы Вариньона и третьего уравнения (76)

и поскольку, в соответствии с предположением 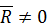, то линия действия должна проходить через точку (штрих-пунктир на рис. 79). Это невозможно, так как точки и не лежат на одной прямой с точкой . Получили противоречие, следовательно, и система сил является уравновешенной.

Уравнения (76) называют третьей формой независимых уравнений равновесия для плоской произвольной системы сил. Здесь моментные точки , и не должны лежать на одной прямой.

Прежде чем рассматривать пример решения задачи, изложим рекомендуемый порядок действий при решении типовых задач статики.

Порядок действий при решении типовых задач статики

1. Выбрать объект равновесия (ОР). В качестве ОР следует выбирать тело (или систему тел), на которое действуют как заданные, так и искомые силы.

2. Обозначить на рисунке заданные внешние силы, действующие на ОР.

3. Мысленно отбросить связи, препятствующие свободному перемещению ОР, и заменить их действие соответствующими реакциями.

4. Определить вид полученной системы сил, выбрать оси координат и записать соответствующие виду системы сил независимые уравнения равновесия.

Пример 9

Рис. 81

Однородный стержень 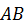длиной 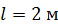и весом 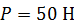закреплен в точке с помощью неподвижного цилиндрического шарнира. Концом стержень опирается на гладкий горизонтальный пол (см. рис. 81). На стержень действуют пара сил с моментом 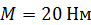и сила 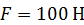, приложенная в центре тяжести стержня перпендикулярно стержню. Найти реакции пола и шарнира , если .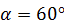

Решение

Проведем решение в соответствии с рекомендованным выше порядком действий.

1. Выберем в качестве ОР стержень .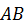

2. Обозначим на рисунке заданные внешние нагрузки, действующие на стержень: пару сил с моментом 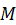, силу 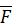и силу тяжести 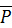, приложенную в центре тяжести стержня.

3. Реакцию цилиндрического шарнира в точке разложим на две составляющих 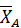, , 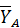реакцию пола 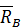направим перпендикулярно полу.

4. Получили плоскую произвольную систему сил. Выберем две оси координат (см. рис. 81) и запишем для полученной системы сил три независимых уравнения равновесия. При записи третьего уравнения равновесия алгебраические моменты сил будем вычислять относительно точки , так как через эту точку проходят линии действия двух неизвестных сил 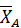, 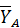. В этом случае третье уравнение будет содержать меньше неизвестных величин.

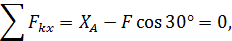
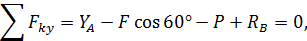
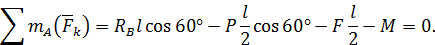
Из полученных трех уравнений легко найти три неизвестные реакции. Из первого уравнения вычислим

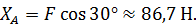
Из третьего уравнения найдем

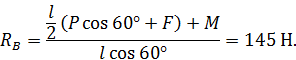
После этого из второго уравнения определим

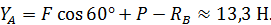
Пример 10

Прямоугольная дверь ABCD весом Р=640 Н, имеющая вертикальную ось вращения АВ, крепится с помощью цилиндрического шарнира в точке А и подпятника в точке В. Дверь открыта на угол САЕ = 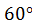и удерживается в этом положении двумя веревками, одна из которых прикреплена к двери в точке С, перекинута через блок Е и натягивается с помощью груза К весом 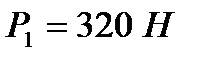, а другая прикреплена к двери в точке D и закреплена в точке F пола под углом 60º к двери. Ширина двери l = АС = 1,8 м, высота h = AB = 2,4 м.

Определить натяжение Т веревки DF , а также реакции цилиндрического шарнира А и подпятника В.

⇐ Предыдущая 1 2 3 4 5 678 Следующая ⇒