
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пример 10 5 страница
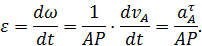
 Рис. 48
Рис. 48
|
 заданы скорость
заданы скорость 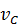 и ускорение
и ускорение 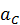 (см. рис. 48).
(см. рис. 48).
Угловая скорость колеса в этом случае найдется по формуле

и в соответствии с направлением вектора  будет направлена по часовой стрелке. Расстояние от точки
будет направлена по часовой стрелке. Расстояние от точки  до мгновенного центра скоростей при движении колеса не меняется и равно радиусу колеса
до мгновенного центра скоростей при движении колеса не меняется и равно радиусу колеса 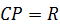 . Тогда угловое ускорение колеса можно найти по формуле
. Тогда угловое ускорение колеса можно найти по формуле
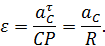
Так как по условию качение колеса является замедленным, то направление углового ускорения будет противоположно направлению угловой скорости (см. рис. 48).
3. Если известно тангенциальное ускорение какой-либо точки  тела при ее относительном вращении вокруг полюса
тела при ее относительном вращении вокруг полюса 
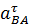 , то угловое ускорение тела найдется по формуле
, то угловое ускорение тела найдется по формуле
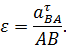
Этот способ вычисления 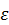 использовался при нахождении углового ускорения шатуна
использовался при нахождении углового ускорения шатуна 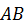 в примере 7.
в примере 7.
Раздел 2. Статика
Статика – это раздел механики, в котором изучается равновесие материальных объектов под действием приложенных сил.
Глава 1. Введение в статику
§ 1.1. Основные понятия
Силой называется векторная величина, характеризующая механическое воздействие одного материального объекта на другой.
Сила характеризуется точкой приложения, направлением действия и численной величиной (модулем).
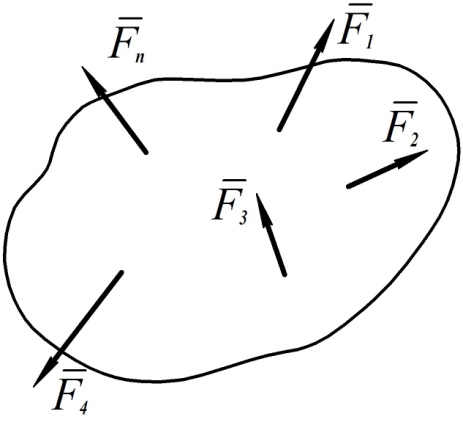 Рис. 49
Рис. 49
|
На рис. 49 изображена система сил, приложенных к некоторому телу.
Будем обозначать систему сил

Две системы сил называются эквивалентными, если, будучи приложенными к твердому телу по отдельности, они сообщают ему одно и то же движение из состояния покоя. Эквивалентность систем сил обозначается знаком 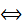 :
:
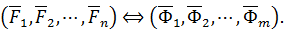
Система сил называется уравновешенной (или эквивалентной нулю), если она, будучи приложенной к твердому телу, не сообщает ему движения из состояния покоя. Уравновешенную систему сил обозначают следующим образом:
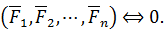
Главным вектором системы сил (обозначается 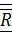 ) называется вектор, равный геометрической сумме всех сил, входящих в систему:
) называется вектор, равный геометрической сумме всех сил, входящих в систему:

| (55) |
На рис. 50 показано геометрическое построение главного вектора системы сил.
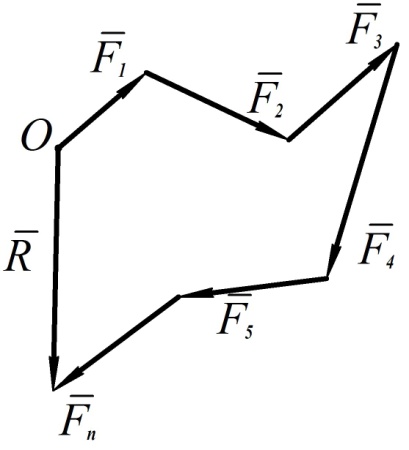 Рис. 50
Рис. 50
|
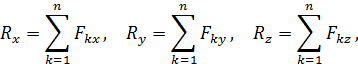
после чего величину главного вектора вычисляют по теореме Пифагора
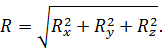
Равнодействующей силой данной системы сил (обозначается 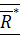 ) называется сила, эквивалентная этой системе сил:
) называется сила, эквивалентная этой системе сил:
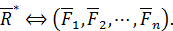
Отметим, что не всякая система сил имеет равнодействующую.
Тело называется свободным, если ничто не препятствует его перемещению в пространстве.
В противном случае тело называется несвободным.
Материальные объекты, ограничивающие перемещение несвободного тела, называются связями.
Силы, с которыми связи действуют на несвободное тело, называются реакциями связей или пассивными силами.
Остальные силы, не являющиеся реакциями связей, называются активными силами.
Активные силы могут сообщать свободному телу движение, они имеют определенный источник действия, не зависят наложенных связей и обычно считаются известными при решении задач.
Реакции связей зависят от активных сил, действующих на несвободное тело, они могут изменять свою величину и направление при изменении активных сил.
§ 1.2. Аксиомы статики
Все основные методы изучения движения и равновесия тел в теоретической механике могут быть строго доказаны математически, исходя из нескольких основных положений, называемых аксиомами. Сами аксиомы сформулированы на основании многовекового опыта человечества. Далее приведем формулировки аксиом статики и дадим необходимые пояснения.
Первая аксиома
Система из двух сил, равных по величине и направленных в противоположные стороны вдоль одной прямой, является уравновешенной.
Эта аксиома справедлива для сил, приложенных к одному абсолютно твердому телу.
Вторая аксиома
Механическое состояние тела не изменится, если к действующей на него системе сил добавить или изъять уравновешенную систему сил.
Исходя из приведенных выше двух аксиом, докажем следствие.
Следствие
Любую силу, не нарушая ее действия на абсолютно твердое тело, можно переносить вдоль линии действия силы.
 Рис. 51
Рис. 51
|
 действует сила
действует сила 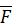 . Возьмем уравновешенную систему сил
. Возьмем уравновешенную систему сил 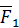 ,
, 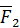 , равных по величине силе
, равных по величине силе 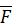 и направленных в противоположные стороны по линии действия силы
и направленных в противоположные стороны по линии действия силы 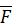 . Приложим обе эти силы в точке
. Приложим обе эти силы в точке  на линии действия силы
на линии действия силы 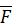 (см. рис. 51).
(см. рис. 51).
Тогда по второй аксиоме
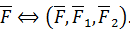
Но по первой аксиоме силы 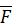 ,
, 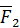 образуют уравновешенную систему и по второй аксиоме их можно отбросить. В результате получим
образуют уравновешенную систему и по второй аксиоме их можно отбросить. В результате получим
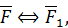
что и доказывает следствие.
Третья аксиома (закон равенства действия и противодействия)
Два тела взаимодействуют с другом с силами, равными по величине и противоположно направленными вдоль одной прямой.
Заметим, что эти силы не будут уравновешенными, так как они приложены к разным телам.
Четвертая аксиома (аксиома параллелограмма сил)
Система из двух сил, приложенных в одной точке тела, имеет равнодействующую силу, равную геометрической сумме двух данных сил.
Эту аксиому можно выразить формулой  и пояснить рисунком
и пояснить рисунком
 Рис. 52
Рис. 52
|
Величину равнодействующей можно вычислить по формуле

Данная аксиома допускает и обратное утверждение:
силу можно по правилу параллелограмма разложить бесчисленным множеством способов на две силы.
При этом составляющие силы могут располагаться в любой одной плоскости, проходящей через линию действия разлагаемой силы.
Пятая аксиома (аксиома связей)
Всякое несвободное тело можно рассматривать как свободное, если связи мысленно отбросить и заменить их действие соответствующими реакциями.
Шестая аксиома (аксиома отвердевания)
Равновесие механической системы не нарушится от наложения новых связей. В частности, равновесие деформируемого тела не нарушится, если оно станет абсолютно твердым.
При этом под механической системой подразумевается выделенная совокупность материальных точек и тел.
§ 1.3. Основные виды связей и их реакции
Встречающиеся на практике связи, ограничивающие перемещение несвободных тел, весьма разнообразны. В механике принята классификация, в соответствии с которой все многообразные связи, встречающиеся в механизмах и конструкциях, подразделяются на небольшое число видов. Связи, внутри одного вида характеризуются аналогичным действием на несвободное тело. Рассмотрим далее основные виды связей в соответствии с этой классификацией и поясним, как правильно заменить их действие на несвободное тело соответствующими реакциями.
1. Гибкая нить
Здесь объединены такие связи как трос, канат, нить, цепь и т. д. Реакцию такой связи называют силой натяжения. Она направлена вдоль нити в случае ее прямолинейности или по касательной к ней, если нить криволинейна (см. рис. 53).
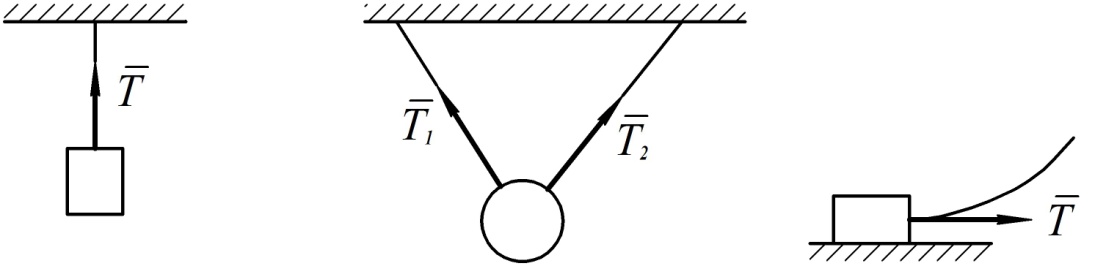 Рис. 53
Рис. 53
|
2. Гладкая поверхность
Здесь имеется в виду абсолютно гладкая поверхность без трения. Реакция такой поверхности направлена перпендикулярно общей касательной плоскости, проведенной в точке контакта с несвободным телом (см. рис. 54). Такую реакцию называют нормальной реакцией.
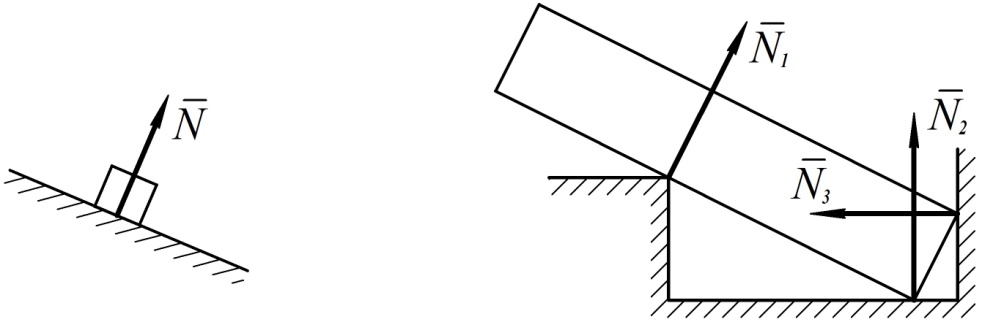 Рис. 54
Рис. 54
|
3. Шероховатая поверхность
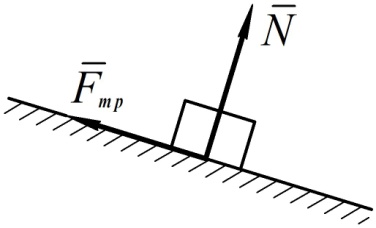 Рис. 55
Рис. 55
|
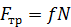 , где
, где 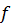 – коэффициент трения скольжения.
– коэффициент трения скольжения.
4. Подвижный шарнир
Шарниром называют устройство, связывающее тела и позволяющее им поворачиваться друг относительно друга. Подвижный шарнир – это такая опора, к которой несвободное тело крепится с помощью шарнира, а сама опора может скользить без трения по опорной поверхности (см. рис. 56). Реакция такой опоры, как и реакция гладкой поверхности, направлена перпендикулярно опорной поверхности, на которую опирается подвижный шарнир.
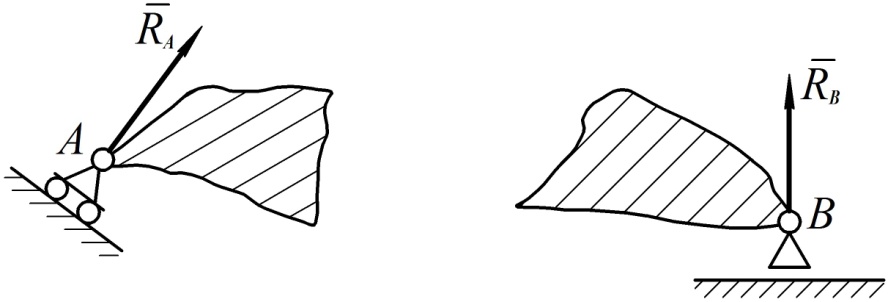 Рис. 56
Рис. 56
|
5. Неподвижный цилиндрический шарнир
Цилиндрический шарнир позволяет скрепленным с его помощью телам поворачиваться друг относительно друга вокруг определенной оси, называемой осью шарнира, и не препятствует перемещению вдоль этой оси. Неподвижный шарнир жестко крепится к неподвижному основанию. Реакция неподвижного цилиндрического шарнира может быть как угодно направлена в плоскости, перпендикулярной оси шарнира. Ее удобно в этой плоскости раскладывать на две взаимно перпендикулярные составляющие (см. рис. 57).
 Рис. 57
Рис. 57
|
6. Неподвижный сферический шарнир
Сферический (шаровой) шарнир позволяет скрепленным с его помощью телам поворачиваться друг относительно друга в любом направлении. Реакция такой опоры может быть как угодно направлена в пространстве. Ее удобно раскладывать на три взаимно перпендикулярные составляющие (см. рис. 58).
7. Подпятник
Это цилиндрический шарнир, который препятствует перемещению несвободного тела вдоль оси шарнира в одном направлении (см. рис. 59). Реакция подпятника раскладывается на три взаимно перпендикулярные составляющие.
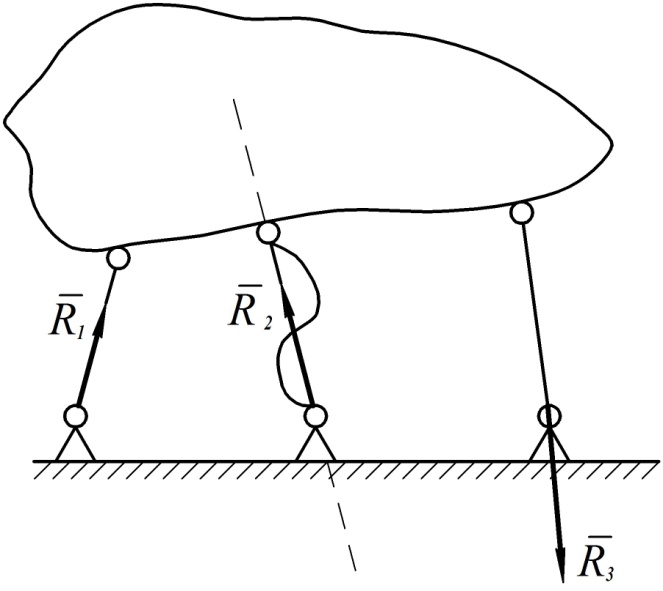 Рис. 60
Рис. 60
|
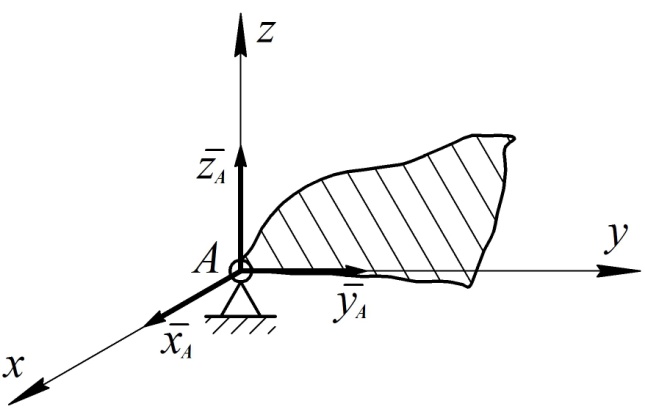 Рис. 58
Рис. 58
|
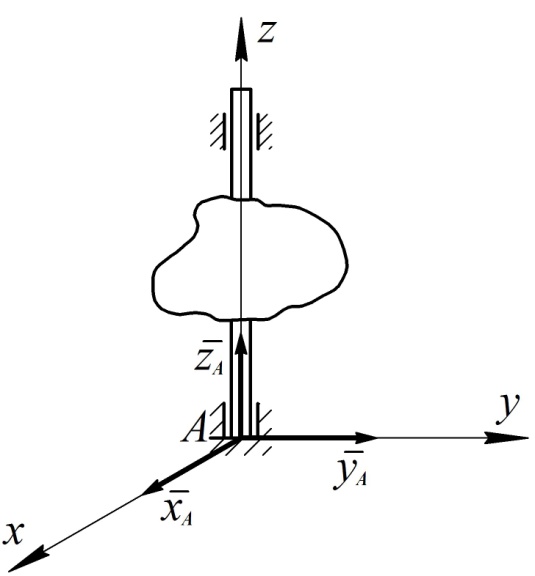 Рис. 59
Рис. 59
|
8. Стержневая опора
Это опора в виде ненагруженного стержня, закрепленного на его концах с помощью шарниров. Реакция такой опоры будет направлена вдоль прямой, проходящей через концы стержня (см. рис. 60). Заметим, что стержень может быть как прямолинейным, так и изогнутым.
9. Жесткая заделка
Это такое крепление несвободного тела, которое не дает ему никакой свободы перемещения. Примером такого крепления может быть сварное соединение или заделка балконной плиты в стену дома. В случае действия на закрепленное таким образом тело плоской системы сил в жесткой заделке возникают реакции, лежащие в той же плоскости. Они включают в себя силу, которую удобно в плоскости действия разложить на две взаимно перпендикулярные составляющие 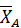 и
и 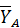 , а также пару сил с моментом
, а также пару сил с моментом 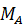 (см. рис. 61). Понятие о паре сил будет дано ниже в главе 4.
(см. рис. 61). Понятие о паре сил будет дано ниже в главе 4.
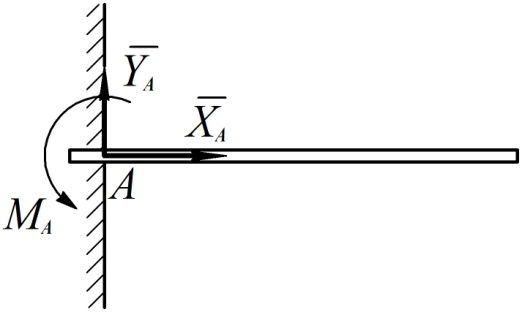 Рис. 61
Рис. 61
|
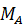 называют моментом заделки. Отметим, что одна часть твердого тела крепится к другой его части (в случае, если тело мысленно расчленить каким-либо сечением) с помощью крепления, аналогичного жесткой заделке.
называют моментом заделки. Отметим, что одна часть твердого тела крепится к другой его части (в случае, если тело мысленно расчленить каким-либо сечением) с помощью крепления, аналогичного жесткой заделке.
В случае, когда на закрепленное с помощью жесткой заделки тело действует пространственная система сил, реакции включают в себя три взаимно перпендикулярные силы 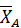 ,
, 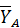 ,
, 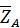 и три пары сил, лежащие в трех координатных плоскостях с моментами
и три пары сил, лежащие в трех координатных плоскостях с моментами 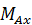 ,
, 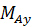 ,
, 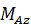 .
.
Глава 2. Система сходящихся сил
§ 2.1. Классификация систем сил
В статике системы сил, действующие на рассматриваемые объекты, классифицируют по расположению в пространстве и по степени сложности.
По расположению в пространстве различают два вида систем сил:
1) плоские системы сил (линии действия всех сил системы лежат в одной плоскости),
2) пространственные системы сил (линии действия всех сил системы не лежат в одной плоскости).
По степени сложности системы сил делят на три категории:
1) сходящиеся системы сил (линии действия всех сил системы пересекаются в одной точке),
2) параллельные системы сил (линии действия всех сил системы параллельны),
3) произвольные системы сил (системы сил наиболее общего вида, не являющиеся сходящимися или параллельными).
В соответствии с этой классификацией различают 6 видов систем сил. В данной главе рассмотрим системы сил простейшего вида – сходящиеся системы сил.
§ 2.2. Приведение сходящейся системы сил к равнодействующей
Пусть к абсолютно твердому телу приложена сходящаяся система сил. Докажем теорему, позволяющую эквивалентным образом упростить такую систему сил.
Теорема
Всякая сходящаяся система сил имеет равнодействующую, равную главному вектору системы сил и приложенную в точке пересечения линий действия сил системы.
Доказательство
Пусть к телу приложена система сил 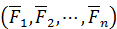 , линии действия которых пересекаются в точке
, линии действия которых пересекаются в точке  (см. рис. 62). Силу
(см. рис. 62). Силу 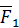 из точки
из точки  можно перенести по линии действия в точку
можно перенести по линии действия в точку  , то же самое можно проделать со всеми остальными силами. В результате этого получим систему сил, приложенных в одной точке
, то же самое можно проделать со всеми остальными силами. В результате этого получим систему сил, приложенных в одной точке  (см. рис. 63).
(см. рис. 63).
 Рис. 62
Рис. 62
|
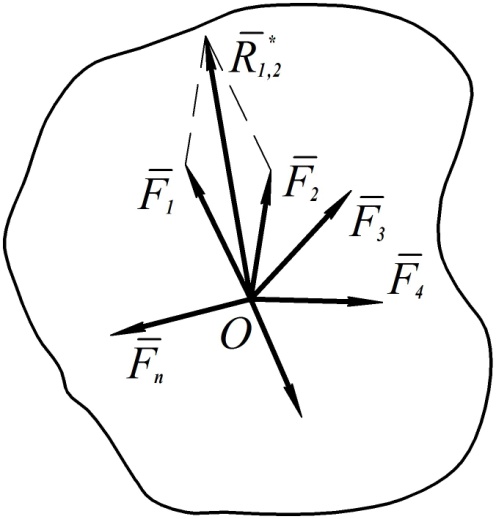 Рис. 63
Рис. 63
|
По третьей аксиоме, силы 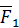 и
и 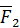 , приложенные в точке
, приложенные в точке  , можно заменить одной равнодействующей силой
, можно заменить одной равнодействующей силой 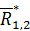 , равной геометрической сумме этих сил:
, равной геометрической сумме этих сил:
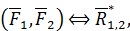
где
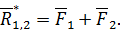
Полученную силу 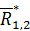 можно аналогично сложить с силой
можно аналогично сложить с силой  :
:
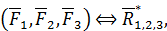
где

Продолжая этот процесс последовательного сложения сил, окончательно получим, что вся исходная сходящаяся система сил эквивалентна одной равнодействующей силе:
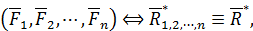
где
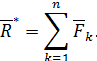
| (56) |
Теорема доказана.
§ 2.3. Уравнения равновесия
Если сходящаяся система сил является уравновешенной, то 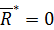 и из (56) вытекает уравнение равновесия в векторной форме
и из (56) вытекает уравнение равновесия в векторной форме
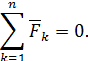
| (57) |
Отсюда легко получить уравнения равновесия в скалярной форме, записав векторное равенство (57) в проекциях на оси координат:

| (58) |
Таким образом, для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы сумма проекций всех сил этой системы на каждую из осей координат равнялась нулю. Если сходящаяся система сил является пространственной, то скалярных уравнений равновесия будет три. Очевидно, что для изучения плоской сходящейся системы сил достаточно в плоскости действия сил выбрать две оси декартовой системы координат и в этом случае будем иметь два скалярных уравнения равновесия:
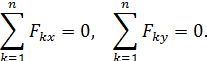
| (59) |
Теорема о трех силах
Если твердое тело находится в равновесии под действием трех сил и линии действия двух из этих сил пересекаются, то линии действия всех трех сил лежат в одной плоскости и пересекаются в одной точке.
Доказательство
Пусть тело находится в равновесии под действием трех сил 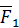 ,
, 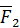 ,
,  и линии действия сил
и линии действия сил 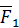 и
и 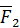 пересекаются в точке
пересекаются в точке  (см. рис. 64).
(см. рис. 64).
Перенесем силы 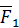 и
и 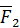 в точку
в точку  и сложим по правилу параллелограмма, заменив равнодействующей силой
и сложим по правилу параллелограмма, заменив равнодействующей силой 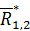 . Тогда имеем соотношение эквивалентности
. Тогда имеем соотношение эквивалентности
 Рис. 64
Рис. 64
|
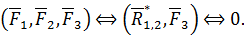
Отсюда, согласно первой аксиоме, следует, что силы  и
и 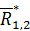 направлены вдоль одной прямой. Следовательно, линия действия силы
направлены вдоль одной прямой. Следовательно, линия действия силы  проходит через точку
проходит через точку  и лежит в плоскости действия сил
и лежит в плоскости действия сил 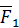 и
и 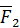 . Теорема доказана.
. Теорема доказана.
Пример 8
Однородный стержень 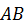 прикреплен к вертикальной стене с помощью шарнира
прикреплен к вертикальной стене с помощью шарнира  и удерживается под углом
и удерживается под углом  к вертикали с помощью нити
к вертикали с помощью нити 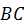 (см. рис. 65). Определить натяжение нити и реакцию шарнира, если задан вес стержня
(см. рис. 65). Определить натяжение нити и реакцию шарнира, если задан вес стержня 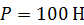 и
и  .
.
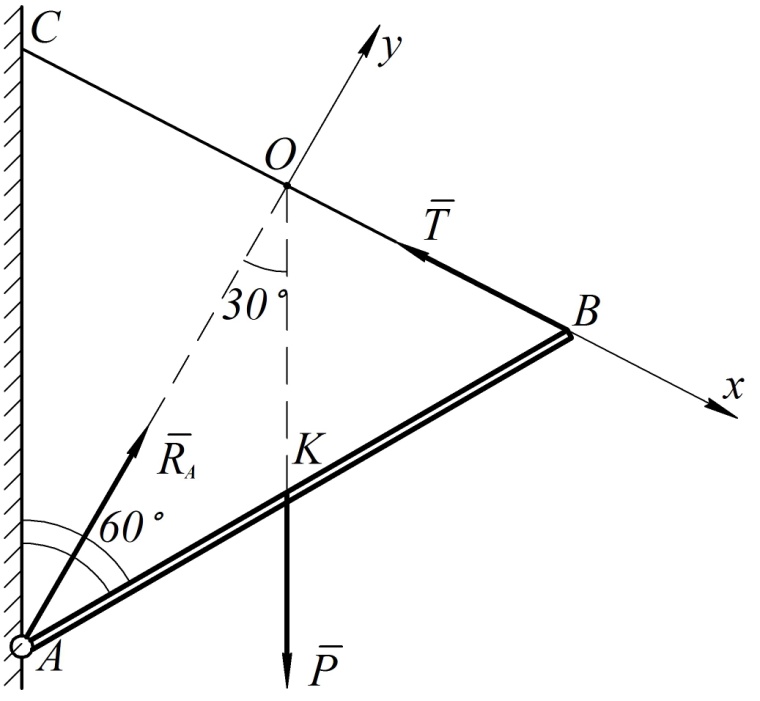 Рис. 65
Рис. 65
|
Рассмотрим равновесие стержня 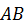 . Он находится в равновесии под действием трех сил: силы тяжести
. Он находится в равновесии под действием трех сил: силы тяжести 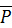 , приложенной в центре тяжести стержня
, приложенной в центре тяжести стержня  и направленной вертикально вниз, силы натяжения нити
и направленной вертикально вниз, силы натяжения нити 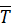 , направленной вдоль нити, и реакции шарнира
, направленной вдоль нити, и реакции шарнира  , направление которой заранее неизвестно. Линии действия сил
, направление которой заранее неизвестно. Линии действия сил 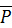 и
и 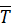 пересекаются в точке
пересекаются в точке  , тогда по теореме о трех силах линия действия реакции шарнира
, тогда по теореме о трех силах линия действия реакции шарнира  тоже проходит через точку
тоже проходит через точку  .
.
Треугольник 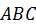 равнобедренный с углом при вершине
равнобедренный с углом при вершине  , то есть равносторонний. Отрезок
, то есть равносторонний. Отрезок 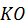 – средняя линия этого треугольника. Поэтому
– средняя линия этого треугольника. Поэтому  является медианой, биссектрисой и высотой треугольника. Следовательно,
является медианой, биссектрисой и высотой треугольника. Следовательно, 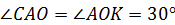 . Проведем оси
. Проведем оси 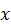 и
и 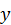 и запишем для полученной плоской сходящейся системы сил уравнения равновесия (59):
и запишем для полученной плоской сходящейся системы сил уравнения равновесия (59):
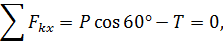

Решая эту систему уравнений, получим  ,
, 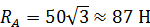 .
.
Глава 3. Момент силы относительно точки и оси
В механике важное значение имеют понятия моментов силы относительно точки и оси. Эти величины характеризуют способность силы поворачивать тело вокруг соответствующей точки или оси.
§ 3.1. Векторный момент силы относительно точки
Векторным моментом силы относительно точки называется вектор, приложенный в этой точке и равный по величине произведению модуля силы на ее плечо относительно моментной точки. Векторный момент силы направлен перпендикулярно плоскости, в которой лежат сила и моментная точка, по правилу правого винта (то есть в ту сторону, откуда видно, что сила стремится повернуть тело вокруг моментной точки против часовой стрелки).
Плечом 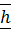 силы относительно точки
силы относительно точки  называется кратчайшее расстояние от этой точки до линии действия силы.
называется кратчайшее расстояние от этой точки до линии действия силы.
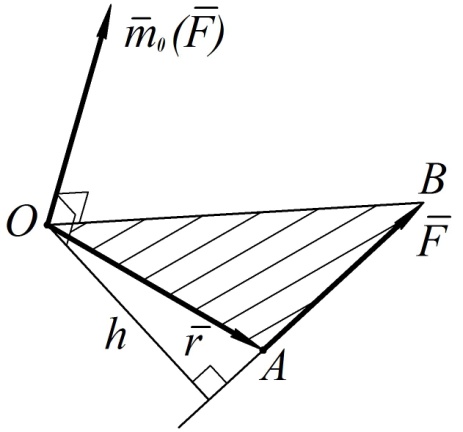 Рис. 66
Рис. 66
|
Обозначив векторный момент силы относительно точки 
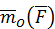 , можно согласно определению для его модуля записать
, можно согласно определению для его модуля записать
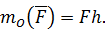
Нетрудно видеть, что модуль векторного момента равен удвоенной площади заштрихованного на рис. 66 треугольника
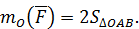
Легко также доказать, что для векторного момента силы справедлива формула

| (60) |
где 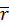 – радиус-вектор точки приложения силы относительно моментной точки
– радиус-вектор точки приложения силы относительно моментной точки  . Вычислим модуль векторного произведения в правой части равенства (60)
. Вычислим модуль векторного произведения в правой части равенства (60)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|