Пример 10 1 страница

Стр 1 из 8Следующая ⇒

Минобрнауки России

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Тверской государственный технический университет»

(ТвГТУ)

В.Е. Клыков

Теоретическая механика

Курс лекций

Часть 1

Учебное пособие

Издание первое

Тверь 2013

УДК 531/534(075.8)

ББК 22.21я7

Клыков, В.Е. Теоретическая механика. Курс лекций. Часть 1: учеб. пособие/ В.Е. Клыков. Тверь: ТвГТУ, 2013. 118 с.

В учебном пособии компактно излагается первая часть курса теоретической механики (кинематика и статика). Содержание курса соответствует государственным образовательным стандартам для специальностей ТМО, ТТ, ЭТК, ГД, КТМ, НТС, СТ, где учебными планами предусмотрено изучение теоретической механики в течение двух учебных семестров. Материал излагается доступно и достаточно строго. Основные положения теории иллюстрируются примерами решения задач.

Пособие предназначено студентам соответствующих специальностей дневной и заочной форм обучения.

Рецензенты: зав. кафедрой СДМО ТвГТУ, доктор технических наук, профессор А.В. Кондратьев; профессор кафедры ремонта машин и ЭМТП ТГСХА, доктор технических наук В.В. Козырев.

ISBN	© Тверской государственный технический университет, 2013 © Клыков В.Е., 2013

Введение

Теоретическая механика – это наука, изучающая математическими методами механическое движение и равновесие материальных объектов. При этом изучаются не реальные материальные тела, а их идеализированные образы – материальная точка и абсолютно твердое тело.

Под материальной точкой понимают материальное тело, размерами которого можно пренебречь.

Абсолютно твердым телом называют такое материальное тело, геометрическая форма и размеры которого не изменяются при любых механических воздействиях со стороны других тел и расстояние между любыми двумя точками которого остается постоянным. В дальнейшем по тексту последний термин не всегда полностью воспроизводится, однако следует иметь в виду, что все рассматриваемые тела считаются абсолютно твердыми.

Такая идеализация изучаемых объектов в теоретической механике делает возможным широкое применение математических методов исследования.

Теоретическая механика имеет фундаментальное значение для науки и техники. На ее законах основываются такие крупные научные области как небесная механика, гидромеханика, механика деформируемого твердого тела. Многие технические науки, такие, как теория машин и механизмов, сопротивление материалов, строительная механика, теория гироскопов и другие, опираются в первую очередь на выводы теоретической механики. Все это делает теоретическую механику одной из важнейших дисциплин инженерно-технического образования.

Содержание теоретической механики включает в себя три раздела: кинематику, статику и динамику. В указанном порядке эти разделы будут рассмотрены далее.

Раздел 1. Кинематика

Кинематика – это раздел теоретической механики, в котором изучается движение материальных объектов с геометрической стороны вне связи с причинами, вызывающими движение.

Глава 1. Кинематика точки

§ 1.1. Векторный способ задания движения точки

Положение точки можно характеризовать радиусом-вектором , который начинается в выбранной неподвижной точке и заканчивается в точке 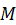, движение которой изучается (рис. 1). При векторном способе задания движения точки её радиус-вектор задаётся как функция времени :

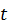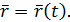
(1)

Уравнение (1) называют векторным уравнением движения точки. Векторная функция в правой его части должна быть дважды дифференцируема.

Покажем далее, как, используя уравнение (1), найти кинематические характеристики движения точки. Попутно дадим определения этим характеристикам движения.

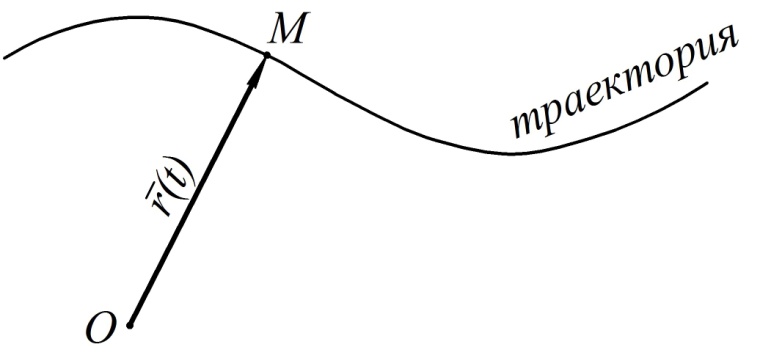Рис. 1

Линия, которую описывает точка при своём движении, называется траекторией. Траектория точки в данном случае может быть найдена как годограф радиус-вектора.

Годографом переменного вектора называется геометрическое место концов этого вектора, если его последовательные положения, получающиеся при изменении аргумента, откладывать из одной неподвижной точки.

Средней скоростью точки за промежуток времени называется вектор

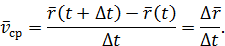
Мгновенной скоростью (или просто скоростью) точки в момент времени 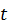называется вектор

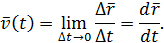
(2)

Рис. 2

Векторы средней и мгновенной скорости показаны на рис. 2.

Вектор скорости характеризует быстроту и направление движения точки. Он направлен по касательной к траектории точки в сторону движения.

Аналогично определяются векторы среднего и мгновенного ускорения точки:

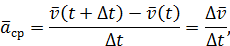
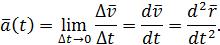
(3)

Рис. 3

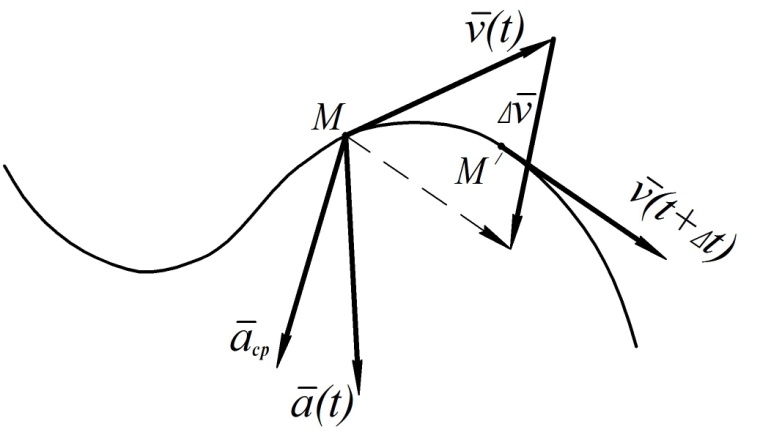Векторы среднего и мгновенного ускорений показаны на рис. 3.

Вектор ускорения характеризует изменение вектора скорости по величине и по направлению. Он отклонен от касательной к траектории в сторону её вогнутости. При прямолинейном движении точки векторы скорости и ускорения направлены вдоль траектории точки.

§ 1.2. Задание движения точки в декартовых координатах

При этом способе задания движения задаются декартовы координаты точки как функции времени:

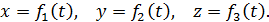
(4)

Уравнения (4) называют кинематическими уравнениями движения точки в декартовых координатах. Функции, стоящие в правых частях этих уравнений, должны быть дважды дифференцируемыми. При движении точки в плоскости достаточно задать два кинематических уравнения движения.

Покажем, как с помощью уравнений (4) можно найти все характеристики движения точки.

Для нахождения траектории нужно из уравнений (4) исключить параметр 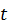. Если точка движется в пространстве, то после исключения 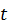из уравнений (4) получим два уравнения вида

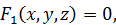
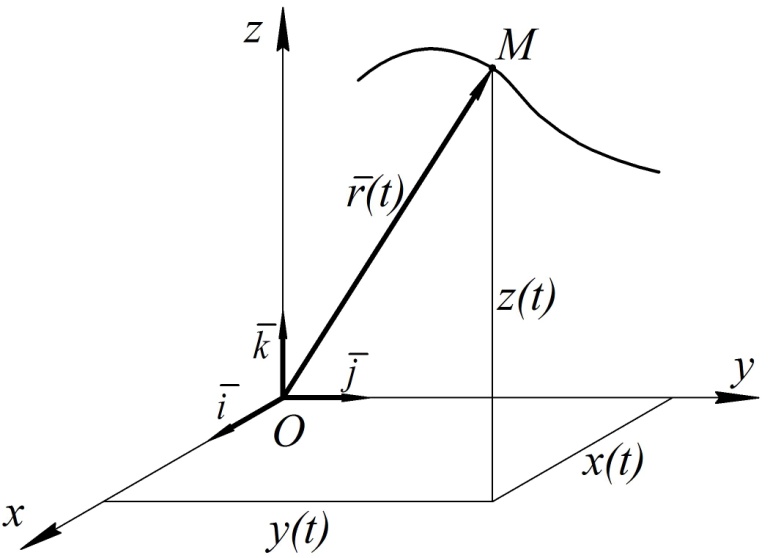Рис. 4

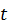Эти уравнения определяют в пространстве линию, которая будет траекторией точки. Если точка движется в плоскости, то после исключения

из первых двух уравнений (4) получим одно уравнение вида

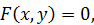
которое определяет линию в плоскости .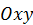

Для нахождения скорости и ускорения точки выразим её радиус-вектор через декартовы координаты. Если в точке , из которой откладывается радиус-вектор, выбрать начало декартовой системы координат, то легко получить выражение (рис. 4)

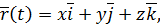
(5)

гд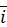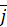е , и – орты координатных осей.

Продифференцировав равенство (5) по времени, получим

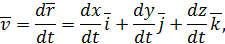
(6)

Обозначая производные по времени точками над дифференцируемой функцией

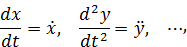
из последнего выражения получим формулы для проекций скорости на оси координат

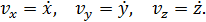
(7)

Величина скорости после этого найдется через её проекции

Повторно дифференцируя равенство (6) по времени, получим

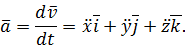
Отсюда проекции ускорения на оси координат

(8)

По этим проекциям определяем величину вектора ускорения

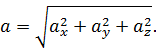
Пример 1

Движение точки в плоскости задано уравнениями

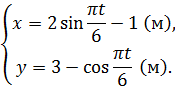
Требуется определить траекторию точки, а также для момента времени 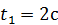найти положение точки, скорость и ускорение.

Решение

Для исключения 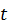из кинематических уравнений движения воспользуемся основным тригонометрическим тождеством

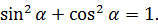
Из уравнений движения выразим

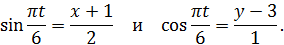
После возведения в квадрат этих выражений и почленного сложения полученных равенств найдем уравнение траектории в виде

Это уравнение эллипса. Построим его на рис. 5.

Положение точки в момент 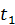определяется её координатами:

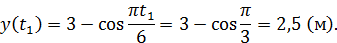
Векторы скорости и ускорения точки найдем через их проекции на оси координат по формулам (7) и (8).

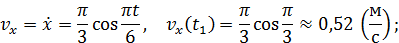
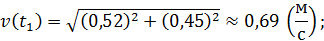
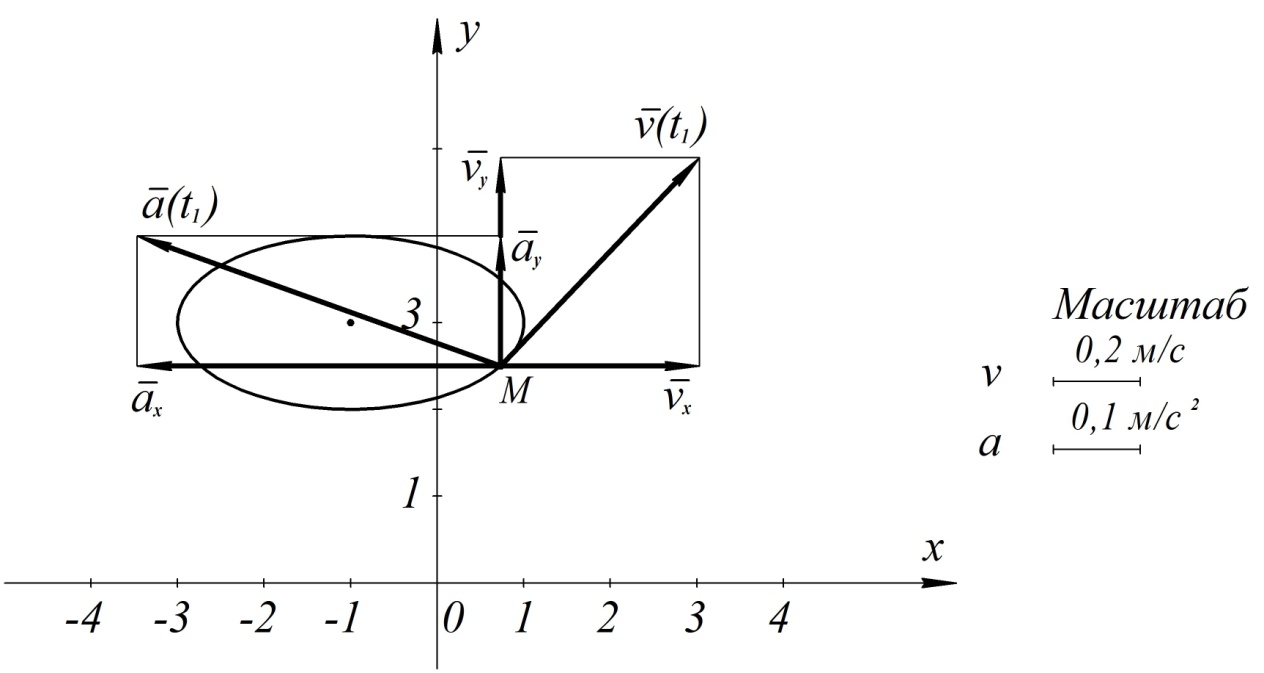Рис. 5

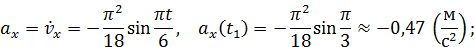
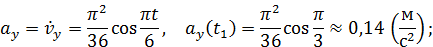
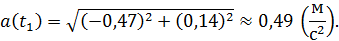
Построим теперь векторы скорости и ускорения в выбранном масштабе на рис. 5, показав их в найденном положении точки на траектории.

§ 1.3. Задание движения точки естественным способом

В этом случае должны быть заданы (рис. 6):

– траектория точки,

– начало отсчета дуговой координаты (точка ) на траектории и положительное направление её отсчета,

– кинематическое уравнение движения в виде

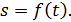
(9)

При данном способе задания движения точки используется естественная система координат, начало которой связано с движущейся точкой (рис. 7).

Эта система координат имеет следующие оси:

– касательная к траектории ;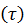

– главная нормаль 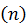, проходящая через центр кривизны траектории;

– бинормаль .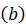

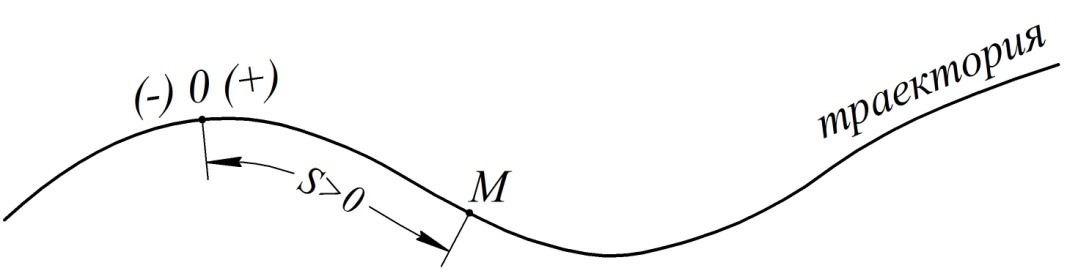Рис. 6

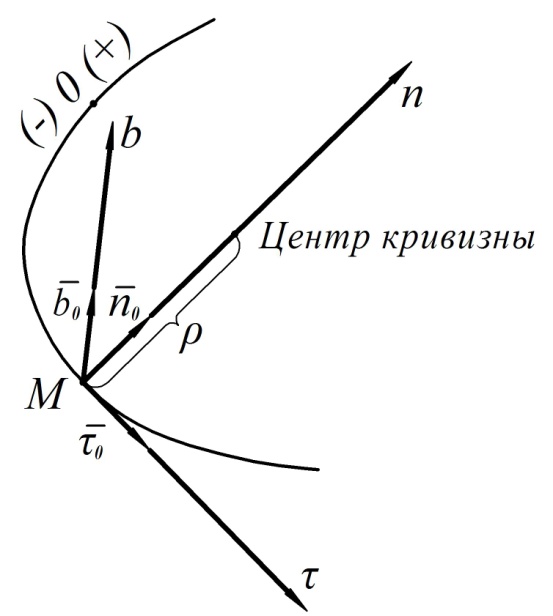Рис. 7

Найдем вектор скорости:

где

как предел отношения бесконечно малой дуги к стягивающей её хорде. Направление вектора 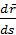установим с учетом того, что вектор 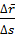направлен по 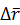при 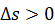и противоположно 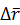при , т.е. вектор 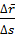по хорде в сторону возрастания дуговой координаты . Следовательно, единичный вектор 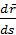направлен по касательной к траектории в направлении оси . Обозначим этот орт оси через 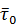. Тогда для скорости точки получим

(10)

где 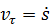– проекция вектора скорости на ось , называемая алгебраической скоростью. Для модуля скорости в данном случае справедлива формула

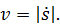
Прежде чем находить ускорение точки, выведем одну вспомогательную формулу для производной от вектора постоянного модуля по скалярному аргументу.

Рассмотрим вектор , где 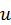– некоторый скалярный аргумент. Пусть вектор имеет постоянный модуль 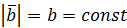, то есть может изменять только своё направление. По определению производной

Для определения 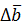из точки отложим векторы и 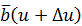(рис. 8) и соединим их концы и . Угол поворота вектора обозначим 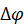. Из равнобедренного треугольника

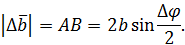
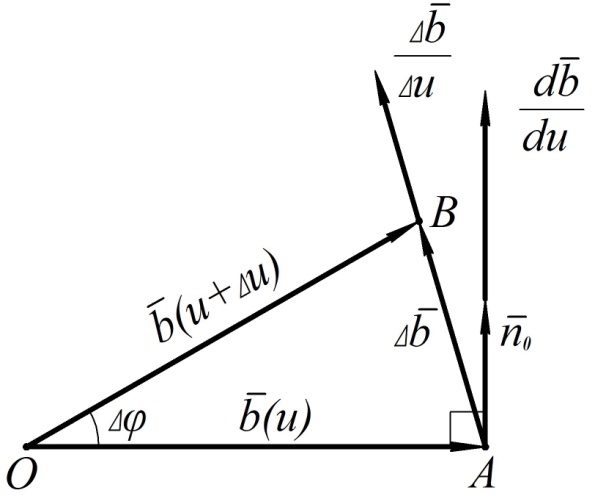Рис. 8

Для модуля искомой производной получим:

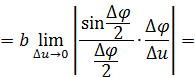
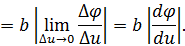
Отметим, что

при 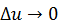.Следовательно, вектор 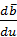направлен перпендикулярно к дифференцируемому вектору в сторону его поворота при изменении аргумента 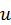(рис. 8).

Окончательно получим формулу

(11)

где 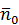– единичный вектор, совпадающий по направлению с вектором .

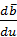Если скалярным аргументом является время 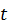, то

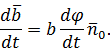
Правую часть этой формулы можно записать в виде векторного произведения двух векторов:

(12)

где 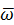– угловая скорость поворота вектора . Величина угловой скорости

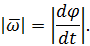
Вектор 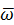следует направить перпендикулярно плоскости, в которой расположены векторы и 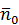, в ту сторону, откуда поворот вектора виден против часовой стрелки.

Определим теперь ускорение точки как производную от вектора скорости по времени, продифференцировав выражение (10):

Преобразуем выражение для производной 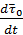с использованием формулы (11):

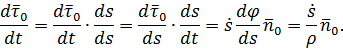
Здесь кривизна траектории 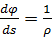выражена через радиус кривизны 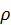. Окончательно для ускорения точки получим векторную формулу

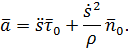
(13)

Отсюда следует, что вектор ускорения точки имеет следующие проекции на оси естественной системы координат:

– проекция ускорения на касательную к траектории, характеризующая изменение вектора скорости по величине:

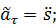
– проекция ускорения на главную нормаль (нормальное ускорение), характеризующая изменение вектора скорости по направлению:

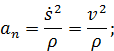
– проекция ускорения на бинормаль, равная нулю при любом движении точки:

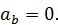
Величину 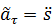, которая может быть как положительной, так и отрицательной, обычно называют алгебраическим значением тангенциального (касательного) ускорения, а величину 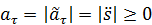называют тангенциальным (касательным) ускорением.

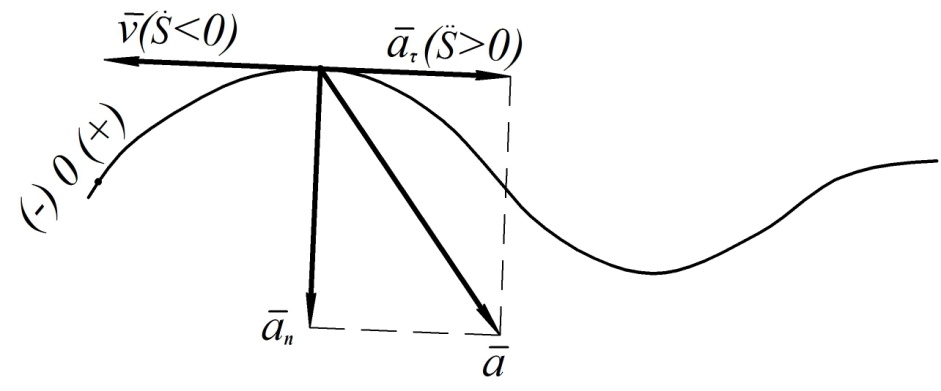Рис. 9

Модуль ускорения вычисляется по формуле

(14)

Все найденные выше характеристики движения точки показаны на рис. 9.

Если векторы и 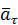направлены в одну сторону, то движение точки называется ускоренным. В противном случае движение точки называют замедленным.

Отметим, что тангенциальное ускорение можно найти и при задании движения точки в декартовых координатах:

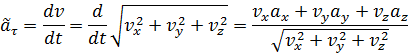
или

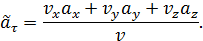
(15)

Найденное по формуле (15) алгебраическое значение тангенциального ускорения может быть как положительной, так и отрицательной величиной. При этом 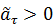соответствует ускоренному, а – замедленному движению точки.

Путь, пройденный точкой за промежуток времени 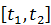, может быть вычислен по формуле

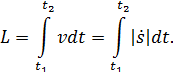
(16)

Далее рассмотрим кратко простейшие случаи движения точки. К ним относятся равномерное и равнопеременное движения.

Признаком равномерного движения является 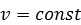. В этом случае при выборе начала отсчета дуговой координаты в начальном положении точки (при 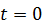) и положительного направления ее отсчета в направлении скорости получим

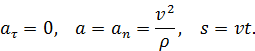
Признаком равнопеременного движения является 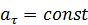. В этом случае при том же выборе начала отсчета и положительного направления отсчета дуговой координаты получим

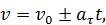
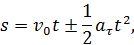
где 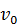– начальная скорость точки; 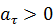; знак « 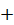» соответствует равноускоренному движению, знак « 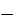» – равнозамедленному.

Пример 2

Движение точки задано кинематическим уравнением

где измеряется в метрах, а 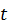– в секундах. Требуется определить путь, пройденный точкой за 4 секунды после начала движения.

Рис. 10

Решение

Вычислим сначала производную

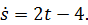
Далее по формуле (16) имеем

Чтобы избавиться от модуля под знаком интеграла, построим график функции на рис. 10.

Теперь можно опустить модуль под знаком интеграла, разбив промежуток интегрирования на две части, и провести вычисления:

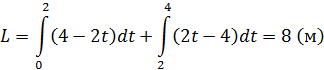
Глава 2. Простейшие движения твердого тела

В теоретической механике движения твердого тела классифицируются по степени сложности. Различают поступательное, вращательное, плоское (плоскопараллельное), сферическое и свободное виды движения.

Поступательное и вращательное движения называют простейшими.

§ 2.1. Поступательное движение твердого тела

Движение твердого тела называется поступательным, если любая прямая, неизменно связанная с телом, во все время движения остается параллельной своему первоначальному положению.

Указанное в определении условие выполняется, если две непараллельные прямые, связанные с телом, остаются параллельными своим первоначальным направлениям. При поступательном движении точки тела могут двигаться по любым траекториям.

Теорема (об основных свойствах поступательного движения)

При поступательном движении твердого тела все его точки движутся по одинаковым траекториям (при наложении совпадающим) и в любой момент времени имеют одинаковые скорости и ускорения.

Доказательство

Выберем на теле, совершающем поступательное движение, две произвольные точки и (рис. 11), в пространстве – неподвижную точку и проведем из нее радиусы-векторы точек и . Нетрудно видеть, что во все время движения справедливо векторное равенство

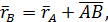
(17)

где вектор имеет постоянный модуль и постоянное направление. Отсюда следует, что траектория точки может быть получена смещением траектории точки на величину вектора .

Продифференцируем теперь векторное равенство (17) по времени, получим

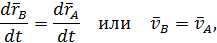
(18)

так как 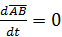. При повторном дифференцировании (18) получим аналогичное соотношение для ускорений точек:

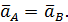
(19)

Теорема доказана

12 3 4 5 6 7 8 Следующая ⇒