
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пример 10 6 страница
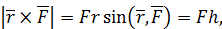
то есть, модули векторов в левой и правой частях равенства (60) равны. Из рис. 66 видно, что и направления этих векторов одинаковы. Таким образом, равенство (60) доказано.
Если выбрать оси декартовой системы координат с началом в точке  , то векторное произведение в (60) можно записать в виде определителя третьего порядка
, то векторное произведение в (60) можно записать в виде определителя третьего порядка
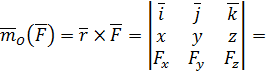
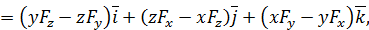
| (61) |
где 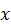 ,
, 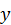 ,
, 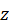 – координаты точки приложения силы
– координаты точки приложения силы  ,
, 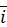 ,
, 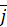 ,
,  – орты координатных осей. Заметим, что выражения в скобках перед ортами в (61) являются проекциями векторного момента на соответствующие оси координат.
– орты координатных осей. Заметим, что выражения в скобках перед ортами в (61) являются проекциями векторного момента на соответствующие оси координат.
Для системы сил вводится понятие главного момента.
Главным моментом системы сил относительно центра  называется вектор, равный геометрической сумме векторных моментов всех сил системы относительно центра
называется вектор, равный геометрической сумме векторных моментов всех сил системы относительно центра  :
:

§ 3.2. Момент силы относительно оси
Моментом силы относительно оси называется взятое со знаком плюс или минус произведение величины проекции силы на плоскость, перпендикулярную оси, на плечо этой проекции относительно рассматриваемой оси. Знак момента определяется по правилу правого винта (знак плюс ставится, если с положительного направления оси видно, что указанная проекция силы стремится повернуть тело вокруг оси против часовой стрелки).
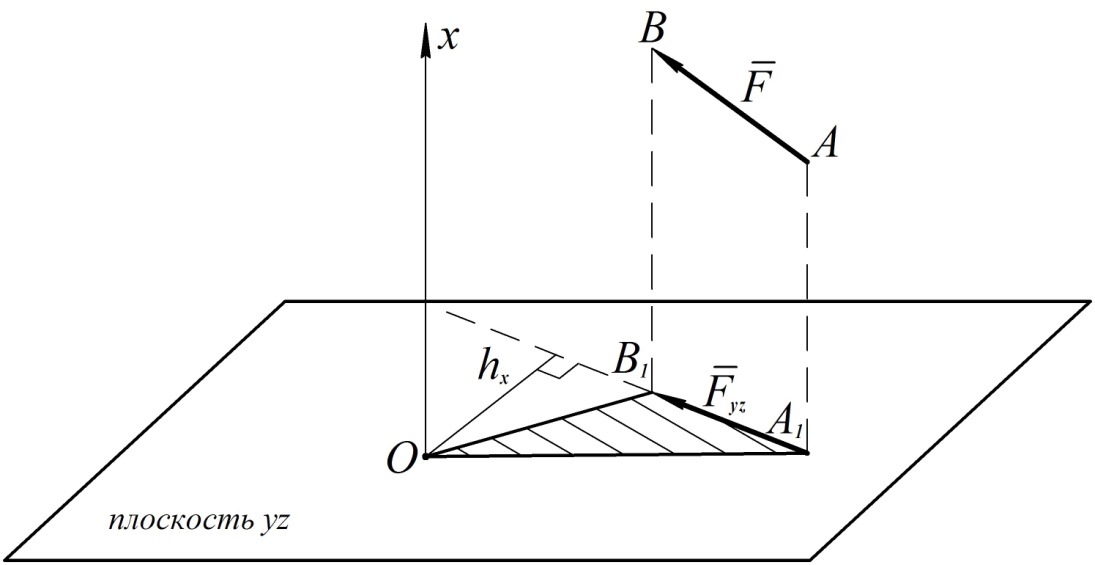 Рис. 67
Рис. 67
|
В соответствии с данным определением для моментов силы относительно осей декартовой системы координат справедливы формулы
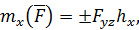
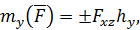
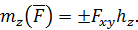
| (62) |
Вычисление момента силы 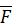 относительно оси
относительно оси 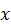 иллюстрируется также рис. 67. В приведенном на рисунке случае момент силы относительно оси
иллюстрируется также рис. 67. В приведенном на рисунке случае момент силы относительно оси 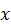 будет положительным.
будет положительным.
Момент силы относительно оси по модулю равен удвоенной площади заштрихованного на рис. 67 треугольника 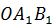 . Из рассмотренного определения следует, что момент силы относительно оси обращается в нуль в двух случаях:
. Из рассмотренного определения следует, что момент силы относительно оси обращается в нуль в двух случаях:
1) когда сила параллельна оси и
2) когда линия действия силы пересекает ось.
Связь между моментом силы относительно оси и векторным моментом силы относительно точки устанавливает следующая теорема.
Теорема
Момент силы относительно оси равен проекции на эту ось векторного момента этой силы, вычисленного относительно любой точки оси.
Доказательство
Изобразим на рис. 68 силу 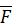 и ось
и ось 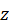 . Выберем на оси
. Выберем на оси 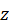 произвольную точку
произвольную точку  и проведем через эту точку плоскость
и проведем через эту точку плоскость  , перпендикулярную оси. Построим проекцию
, перпендикулярную оси. Построим проекцию 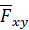 силы
силы 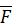 на эту плоскость.
на эту плоскость.
 Рис. 68
Рис. 68
|
Векторный момент  направлен перпендикулярно к плоскости треугольника
направлен перпендикулярно к плоскости треугольника  и равен по модулю удвоенной площади этого треугольника. Момент силы
и равен по модулю удвоенной площади этого треугольника. Момент силы 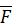 относительно оси
относительно оси 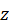 численно равен удвоенной площади треугольника
численно равен удвоенной площади треугольника 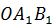 и для изображенного на рис. 68 случая будет положительным. При этом треугольник
и для изображенного на рис. 68 случая будет положительным. При этом треугольник 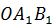 является проекцией треугольника
является проекцией треугольника 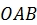 на плоскость
на плоскость  . Из геометрии известно, что площадь проекции плоской фигуры равна площади проецируемой фигуры, умноженной на косинус угла между плоскостями, в которых эти фигуры расположены. Угол между плоскостями измеряется углом между перпендикулярами к этим плоскостям. Угол между плоскостями рассматриваемых треугольников обозначен на рис. 58 буквой
. Из геометрии известно, что площадь проекции плоской фигуры равна площади проецируемой фигуры, умноженной на косинус угла между плоскостями, в которых эти фигуры расположены. Угол между плоскостями измеряется углом между перпендикулярами к этим плоскостям. Угол между плоскостями рассматриваемых треугольников обозначен на рис. 58 буквой 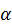 . Таким образом, для момента силы относительно оси
. Таким образом, для момента силы относительно оси 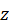 получим
получим
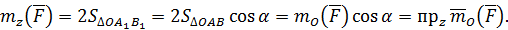
Теорема доказана.
Из этой теоремы следует, что момент силы относительно координатных осей можно вычислять не только по формулам (62), но и еще двумя способами. Исходя из выражения (61) по формулам
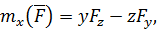
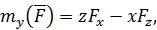
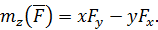
| (63) |
А также через векторный момент силы относительно начала координат

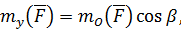

| (64) |
где 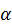 ,
, 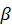 ,
,  – углы, составляемые векторным моментом силы
– углы, составляемые векторным моментом силы 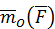 с соответствующими координатными осями.
с соответствующими координатными осями.
§ 3.3. Алгебраический момент силы относительно точки
При изучении плоских систем сил рассматривают алгебраический момент силы относительно моментной точки, лежащей в плоскости действия сил.
Алгебраическим моментом силы относительно точки называется взятое со знаком плюс или минус произведение модуля силы на ее плечо относительно моментной точки. Знак плюс выбирается, если сила стремится повернуть тело вокруг моментной точки против движения часовой стрелки.
Вычисление алгебраического момента силы поясняется на рис. 69. В соответствии с рисунком для алгебраических моментов силы 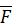 относительно точек
относительно точек  ,
,  и
и  имеем
имеем

| (65) |
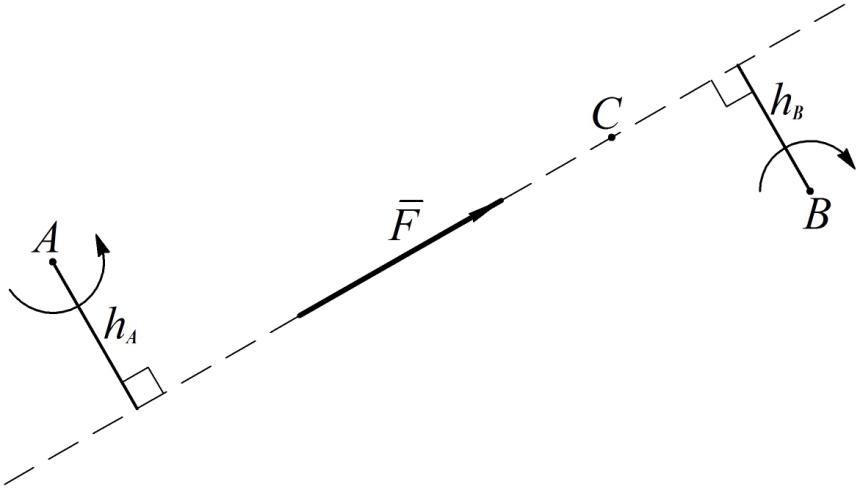 Рис. 69
Рис. 69
|
Отметим, что алгебраический момент силы относительно точки равен моменту силы относительно оси, проведенной перпендикулярно плоскости действия сил к нам. По указанным выше правилам можно вычислять векторный, относительно оси и алгебраический моменты не только для вектора силы, но и для любого другого вектора.
Глава 4. Пара сил и ее свойства
§ 4.1. Понятие о паре сил
Парой сил называется система из двух равных по величине сил, направленных в противоположные стороны вдоль параллельных прямых.
Пара сил – это неупрощаемая система сил (её действие на тело нельзя эквивалентным образом заменить действием одной равнодействующей силы). Она стремится придать телу вращательное движение из состояния покоя. Пару сил в механике рассматривают как одно из основных понятий наряду с понятием силы. Действие пары сил на тело характеризуется её векторным моментом.
Векторным моментом пары сил называется вектор, равный по величине произведению модуля одной из сил пары на плечо пары сил. Векторный момент пары сил направлен перпендикулярно плоскости действия пары сил по правилу правого винта (в ту сторону, откуда видно, что пара сил стремится повернуть тело против часовой стрелки).
Плечом 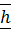 пары сил называется расстояние между линиями действия сил, составляющих пару.
пары сил называется расстояние между линиями действия сил, составляющих пару.
Схематически пара сил и её векторный момент показаны на рис. 70.
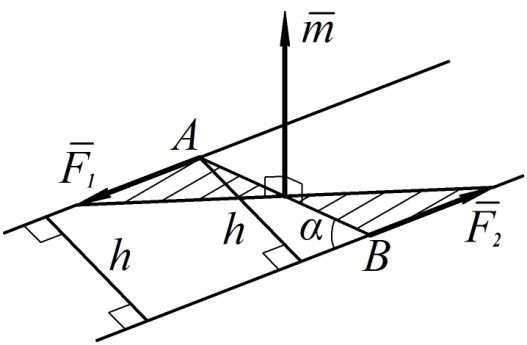 Рис. 70
Рис. 70
|
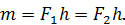
| (66) |
Легко доказать, что векторный момент пары сил можно выразить в виде векторного произведения по формуле (см. рис. 69)
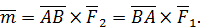
| (67) |
Действительно, модуль такого векторного произведения

совпадает с величиной векторного момента (см. формулу (66)). Направление каждого из векторных произведений в (67) тоже совпадает с направлением векторного момента пары сил (см. рис. 70).
При рассмотрении плоских систем сил, в состав которых входят пары сил, вводится понятие алгебраического момента пары сил.
Алгебраическим моментом пары сил называется взятое со знаком плюс или минус произведение модуля одной из сил пары на плечо пары сил. Знак алгебраического момента пары сил определяется по правилу правого винта (момент считается положительным, если пара сил стремится повернуть тело против часовой стрелки).
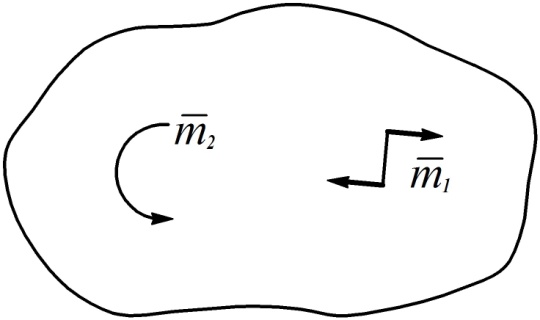 Рис. 71
Рис. 71
|

| (68) |
На рисунках и расчетных схемах пару сил обозначают либо её векторным моментом, либо одним из значков, показанных на рис. 71, расположенным в плоскости действия пары сил.
§ 4.2. Основные свойства пар сил
Можно доказать, что пара сил, приложенная к твердому телу, обладает следующими свойствами.
1. Пару сил, не изменяя её действия на тело, можно как угодно поворачивать и переносить в плоскости её действия в пределах тела.
2. Пару сил, не изменяя её действия на тело, можно переносить в пределах тела из плоскости её действия в параллельную плоскость.
3. Не изменяя действия пары сил на тело, можно одновременно изменять величину сил пары и её плечо так, чтобы величина её момента оставалась неизменной.
Отсюда следует, что действие пары сил на тело полностью характеризуется её векторным моментом.
Докажем далее две важные теоремы о свойствах пар сил.
Теорема о сложении пар сил
Две пары сил, действующие на твердое тело, можно эквивалентным образом заменить одной парой сил, векторный момент которой равен геометрической сумме векторных моментов исходных пар сил.
Доказательство
Пусть имеется две пары сил  ,
,  , лежащие в пересекающихся плоскостях (см. рис. 72).
, лежащие в пересекающихся плоскостях (см. рис. 72).
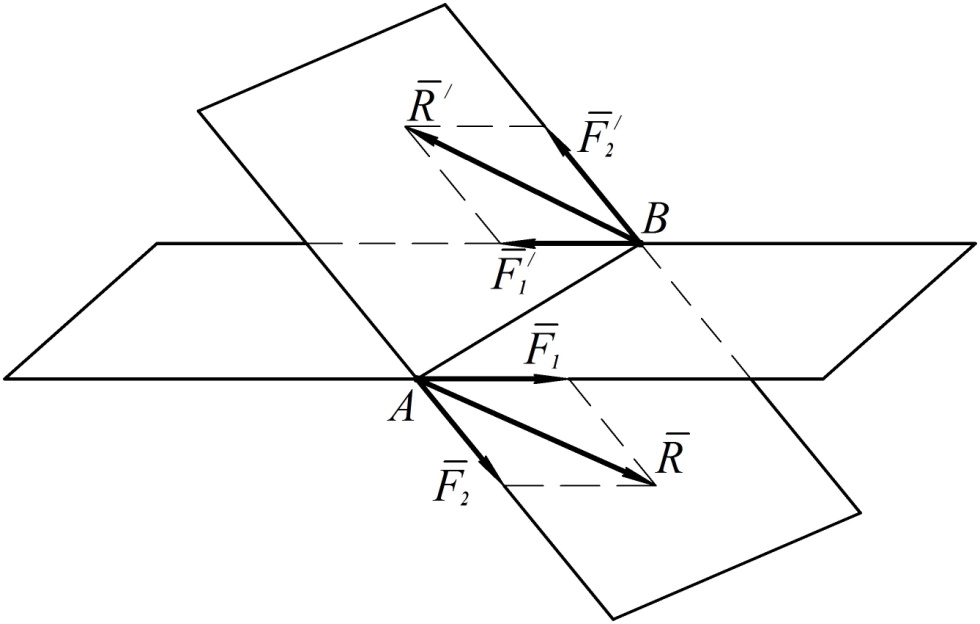 Рис. 72
Рис. 72
|
Такие пары сил можно получить из пар сил, как угодно расположенных в пересекающихся плоскостях, путем параллельного переноса, поворота в плоскости действия и одновременного изменения плеч и величин сил пар. Сложим геометрически силы в точках  и
и  . Получим две силы
. Получим две силы 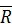 и
и 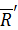 , эквивалентные исходным четырем силам. Силы
, эквивалентные исходным четырем силам. Силы 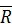 и
и 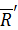 составляют пару сил, так как
составляют пару сил, так как
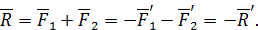
Моменты исходных пар сил можно выразить в виде векторных произведений
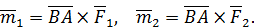
Для момента эквивалентной пары сил можно записать
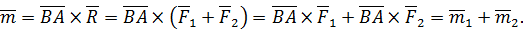
Теорема доказана.
Применяя последовательно эту теорему, можно любое количество пар сил заменить одной эквивалентной парой сил, векторный момент которой равен геометрической сумме векторных моментов исходных пар сил.
Теорема о сумме моментов сил пары
Геометрическая сумма векторных моментов сил, составляющих пару, относительно любой точки пространства равна векторному моменту пары сил.
Доказательство
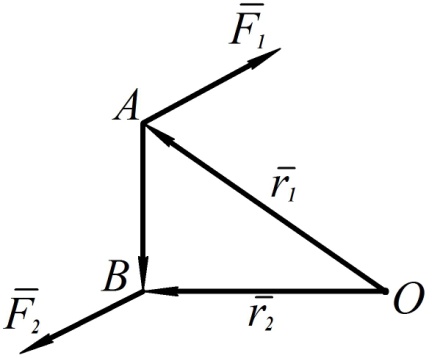 Рис. 73
Рис. 73
|
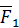 и
и 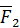 относительно произвольно выбранной точки
относительно произвольно выбранной точки 
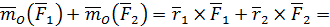

так как для пары сил 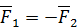 . Кроме того,
. Кроме того,  независимо от выбора точки О
независимо от выбора точки О
что и требовалось доказать.
Отметим, что при рассмотрении пар сил, расположенных в одной плоскости, в формулировках двух последних теорем следует векторные моменты заменить на алгебраические.
Глава 5. Приведение системы сил к центру
§ 5.1. Приведение произвольной пространственной системы сил к центру
Лемма Пуансо
Силу можно переносить параллельно самой себе в любую точку твердого тела, добавляя при этом пару сил, векторный момент которой равен векторному моменту переносимой силы относительно новой точки приложения.
Доказательство
 Рис. 74
Рис. 74
|
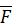 , приложенную к твердому телу в точке
, приложенную к твердому телу в точке  (см. рис. 74). Приложим в точке
(см. рис. 74). Приложим в точке  тела две равные по величине и противоположно направленные силы
тела две равные по величине и противоположно направленные силы 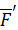 и
и 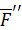 , параллельные исходной силе
, параллельные исходной силе 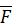 . При этом по величине
. При этом по величине 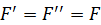 . Заметим, что силы
. Заметим, что силы 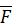 ,
, 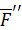 составляют пару сил, которую называют присоединенной парой сил. Очевидно, что векторный момент этой пары сил равен векторному моменту силы
составляют пару сил, которую называют присоединенной парой сил. Очевидно, что векторный момент этой пары сил равен векторному моменту силы 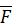 относительно точки
относительно точки 
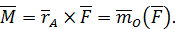
В результате можно записать соотношение эквивалентности
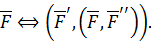
Итак, мы силу 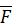 , приложенную к твердому телу в точке
, приложенную к твердому телу в точке  , эквивалентным образом заменили силой
, эквивалентным образом заменили силой 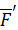 , равной ей по величине и одинаковой по направлению, но приложенной в точке
, равной ей по величине и одинаковой по направлению, но приложенной в точке  , и присоединенной парой сил
, и присоединенной парой сил 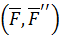 , векторный момент которой равен векторному моменту исходной силы
, векторный момент которой равен векторному моменту исходной силы 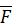 относительно точки
относительно точки  . Лемма доказана.
. Лемма доказана.
Указанный в лемме процесс замены силы 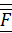 силой
силой 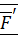 , приложенной в точке
, приложенной в точке  , и парой сил
, и парой сил 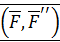 называют приведением силы
называют приведением силы 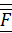 к центру
к центру  .
.
Теорема Пуансо (основная теорема статики)
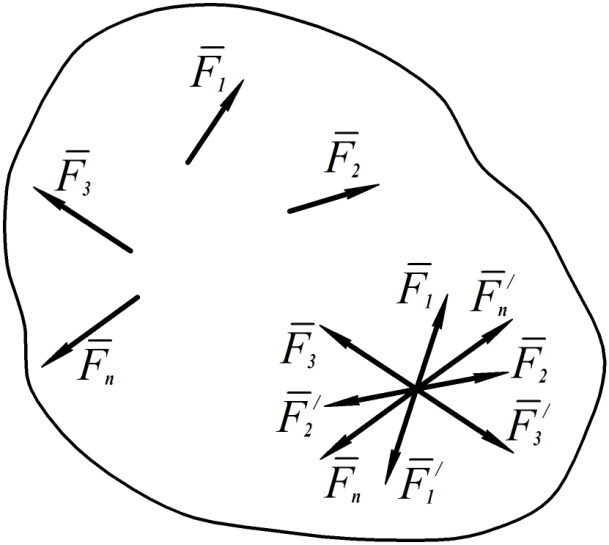 Рис. 75
Рис. 75
|
Доказательство
Пусть к твердому телу приложена произвольная система сил 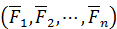 . Выберем произвольную точку
. Выберем произвольную точку  тела за центр приведения и каждую силу заданной системы сил приведем к точке
тела за центр приведения и каждую силу заданной системы сил приведем к точке  (см. рис. 75).
(см. рис. 75).
В результате получим, что исходная система сил эквивалентным образом заменена системой из 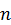 сходящихся сил, приложенных в точке
сходящихся сил, приложенных в точке  , и системой из
, и системой из 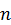 присоединенных пар сил:
присоединенных пар сил:
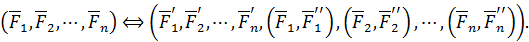
Далее систему сходящихся сил 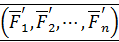 заменим одной равнодействующей силой
заменим одной равнодействующей силой 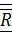 , называемой главным вектором исходной системы сил и равной геометрической сумме сил системы:
, называемой главным вектором исходной системы сил и равной геометрической сумме сил системы:

где
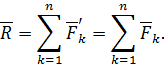
| (69) |
Систему присоединенных пар сил по теореме о сложении пар сил заменим одной парой сил 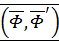 , векторный момент которой
, векторный момент которой 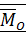 называется главным моментом исходной системы сил относительно центра
называется главным моментом исходной системы сил относительно центра  и вычисляется как геометрическая сумма векторных моментов складываемых пар сил:
и вычисляется как геометрическая сумма векторных моментов складываемых пар сил:
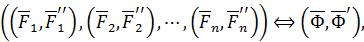
где
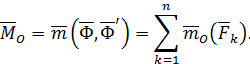
| (70) |
Таким образом, окончательно имеем
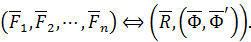
Теорема доказана.
§ 5.2. Частные случаи приведения системы сил к центру
По доказанной выше основной теореме статике любую систему сил можно эквивалентным образом заменить одной силой и одной парой сил. Применяя этот метод на практике, можно получить различные частные случаи, характеризующие свойства исходной упрощаемой системы сил. Рассмотрим эти частные случаи более подробно.
1. Пусть в результате вычисления главного вектора и главного момента системы сил по формулам (69), (70) получилось

В этом случае система сил является уравновешенной, она не сообщает телу движения из состояния покоя.
2. Пусть в результате приведения системы сил к центру получено
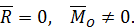
В этом случае говорят, что система сил приводится к паре сил. Такая система сил стремится сообщить телу вращательное движение из состояния покоя.
3. Пусть в результате приведения системы сил к центру получено
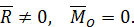
В этом случае система сил приводится к равнодействующей, равной главному вектору. При этом линия действия равнодействующей проходит через выбранный центр приведения  .
.
4. Пусть в результате приведения системы сил к центру получено
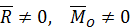
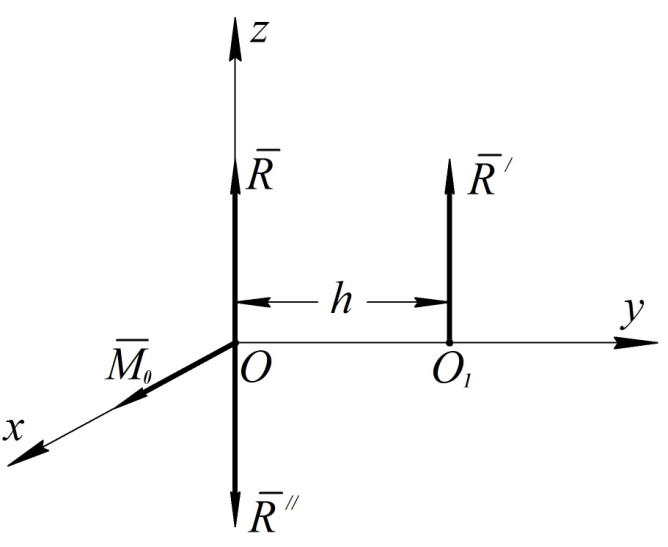 Рис. 76
Рис. 76
|
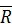 перпендикулярен главному моменту
перпендикулярен главному моменту 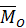 . Покажем, что и в этом случае система сил приводится к равнодействующей, но линия ее действия не проходит через центр приведения
. Покажем, что и в этом случае система сил приводится к равнодействующей, но линия ее действия не проходит через центр приведения  . Изобразим главный вектор и главный момент на рис. 76, выбрав соответствующие оси координат.
. Изобразим главный вектор и главный момент на рис. 76, выбрав соответствующие оси координат.
Пару сил, соответствующую главному моменту, выберем так, чтобы величины сил пары были равны величине главного вектора 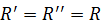 , и вектор
, и вектор 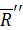 приложим в центре приведения
приложим в центре приведения  , направив его противоположно главному вектору
, направив его противоположно главному вектору 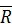 . Плечо такой пары сил определится по формуле
. Плечо такой пары сил определится по формуле
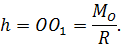
Отбрасывая силы 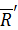 и
и 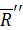 , приложенные в точке
, приложенные в точке  , получим, что исходная система сил эквивалентна одной равнодействующей силе
, получим, что исходная система сил эквивалентна одной равнодействующей силе 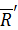 , равной главному вектору и приложенной в точке
, равной главному вектору и приложенной в точке  .
.
5. Пусть в результате приведения системы сил к центру получено
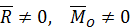
и главный вектор системы сил 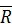 не перпендикулярен главному моменту
не перпендикулярен главному моменту 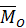 .
.
Выберем оси координат так, чтобы векторы 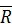 и
и 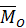 располагались в плоскости
располагались в плоскости 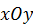 (см. рис. 77).
(см. рис. 77).
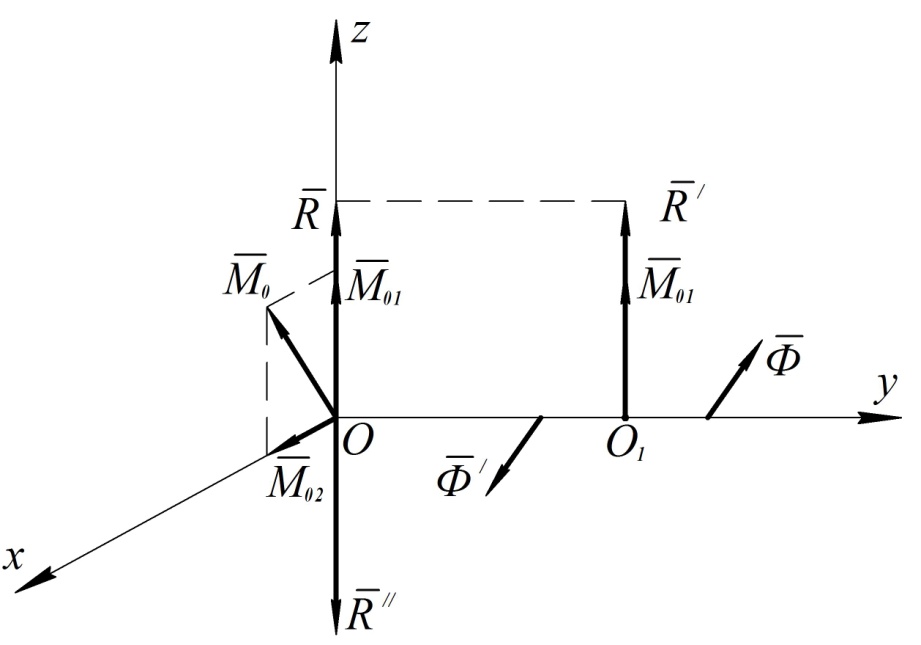 Рис. 77
Рис. 77
|
Разложим теперь главный момент 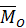 на два взаимно перпендикулярных момента
на два взаимно перпендикулярных момента  и
и  согласно теореме о сложении пар сил. Каждому из этих моментов соответствует своя пара сил. Пару сил, соответствующую моменту
согласно теореме о сложении пар сил. Каждому из этих моментов соответствует своя пара сил. Пару сил, соответствующую моменту  , выберем так, чтобы величины сил пары были равны величине главного вектора
, выберем так, чтобы величины сил пары были равны величине главного вектора 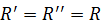 , и вектор
, и вектор 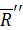 приложим в центре приведения
приложим в центре приведения  , направив его противоположно главному вектору
, направив его противоположно главному вектору 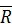 . Плечо такой пары сил определится по формуле
. Плечо такой пары сил определится по формуле
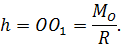
Отбрасывая силы 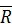 и
и 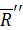 , приложенные в точке
, приложенные в точке  , получим, что исходная система сил эквивалентна силе
, получим, что исходная система сил эквивалентна силе 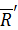 и паре сил
и паре сил  с моментом
с моментом  , параллельным этой силе.
, параллельным этой силе.
Такая совокупность силы  и пары сил
и пары сил 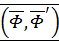 , плоскость действия которой перпендикулярна силе, называется динамическим винтом или динамой. Прямая, проходящая через точку
, плоскость действия которой перпендикулярна силе, называется динамическим винтом или динамой. Прямая, проходящая через точку 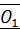 , вдоль которой направлены векторы
, вдоль которой направлены векторы  и
и 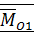 , называется осью динамического винта. Соответствующая система сил стремится сообщить телу винтовое движение из состояния покоя.
, называется осью динамического винта. Соответствующая система сил стремится сообщить телу винтовое движение из состояния покоя.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|