
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пример 10 4 страница
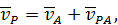
где вектор 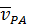 перпендикулярен отрезку
перпендикулярен отрезку  и направлен противоположно вектору
и направлен противоположно вектору 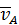 . Найдем модуль вектора
. Найдем модуль вектора 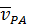
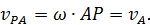
Таким образом, получаем, что 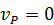 . Мгновенный центр скоростей (точка
. Мгновенный центр скоростей (точка  ) построен. Теорема доказана.
) построен. Теорема доказана.
Если мгновенный центр скоростей известен, то приняв его за полюс, для точки  плоской фигуры получим
плоской фигуры получим
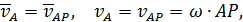
| (46) |
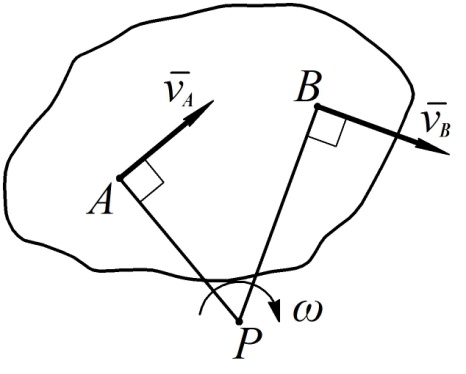 Рис. 37
Рис. 37
|
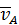 перпендикулярна к отрезку
перпендикулярна к отрезку  . Аналогично и для любой другой точки
. Аналогично и для любой другой точки 
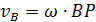
| (47) |
и вектор 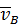 перпендикулярен отрезку
перпендикулярен отрезку 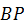 (см. рис. 37).
(см. рис. 37).
Из (46) и (47) следует, что
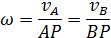
| (48) |
и
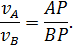
| (49) |
Следовательно, скорости точек фигуры при плоском движении могут вычисляться как при вращении этой фигуры в данный момент вокруг мгновенного центра скоростей с угловой скоростью 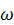 .
.
Таким образом, если построен МЦС и найдена угловая скорость, вычисление скоростей точек тела при плоском движении существенно упрощается. Угловая скорость обычно находится после построения МЦС по формуле (48). Рассмотрим далее основные способы построения МЦС.
Основные способы построения МЦС
1. Один способ уже рассмотрен при доказательстве теоремы о существовании МЦС.
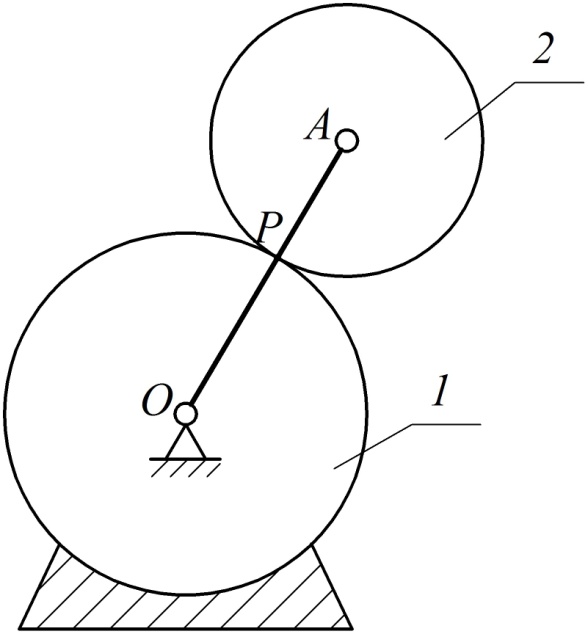 Рис. 38
Рис. 38
|
 является мгновенным центром скоростей для тела 2.
является мгновенным центром скоростей для тела 2.
3. Если известны направления скоростей в двух точках тела, то, как видно из рис. 37, мгновенный центр скоростей найдется как точка пересечения перпендикуляров к скоростям этих точек тела. Этот способ нахождения МЦС чаще всего используется на практике. Здесь следует отметить два частных случая.
3.а. Если точки лежат на общем перпендикуляре к скоростям этих точек, нужно дополнительно знать величины скоростей. В этом случае МЦС найдется как точка пересечения общего перпендикуляра к скоростям и прямой, проведенной через концы векторов скоростей точек, изображенных в выбранном масштабе (см. рис. 39). Этот способ построения следует из пропорциональности скоростей точек тела расстояниям от этих точек до МЦС (см. формулу (49)).
3.б. Если перпендикуляры к скоростям точек тела (случай 3) или общий перпендикуляр к скоростям точек и прямая, проведенная через концы векторов скоростей, (случай 3.а) параллельны, то говорят, что МЦС находится в бесконечности (см. рис. 40).
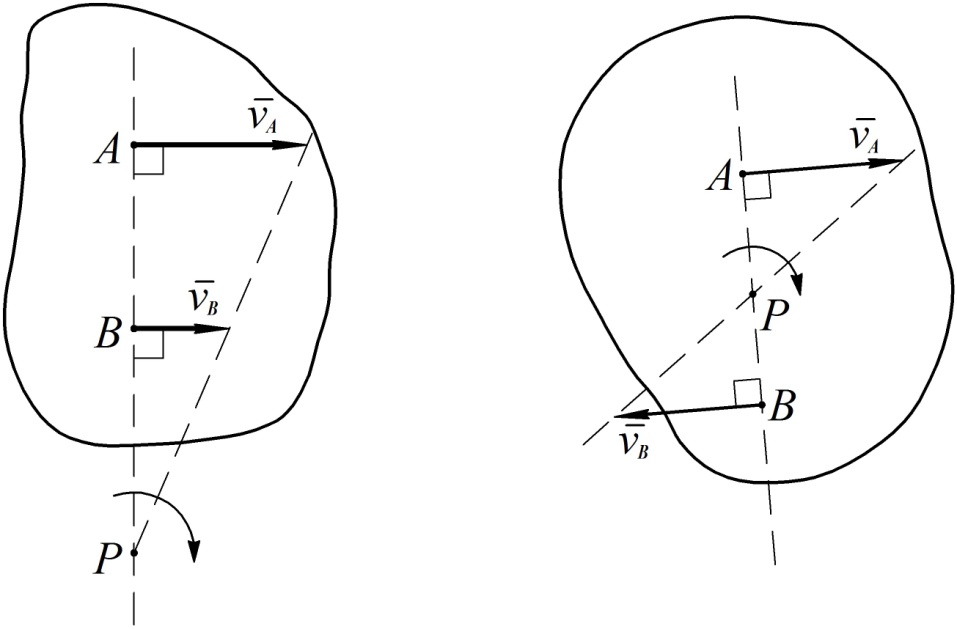 Рис. 39
Рис. 39
|
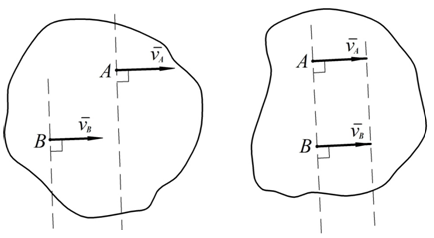 Рис. 40
Рис. 40
|
В этом случае движение тела называют мгновенно-поступательным. При мгновенно-поступательном движении угловая скорость тела равна нулю
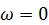
и скорости всех точек тела равны по величине и одинаково направлены
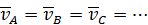
Заметим, что при мгновенно-поступательном движении в отличие от поступательного траектории различных точек тела и их ускорения не будут одинаковыми.
Пример 6
Кривошип  длиной
длиной 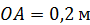 вращается вокруг неподвижной оси
вращается вокруг неподвижной оси  с угловой скоростью
с угловой скоростью 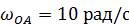 . C помощью шатуна
. C помощью шатуна 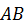 кривошип приводит в движение диск радиуса
кривошип приводит в движение диск радиуса 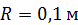 , катящийся по горизонтальной плоскости без проскальзывания. В положении, указанном на рисунке 41 (когда кривошип вертикален, а шатун горизонтален), найти угловую скорость диска и скорости точек
, катящийся по горизонтальной плоскости без проскальзывания. В положении, указанном на рисунке 41 (когда кривошип вертикален, а шатун горизонтален), найти угловую скорость диска и скорости точек  и
и 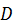 .
.
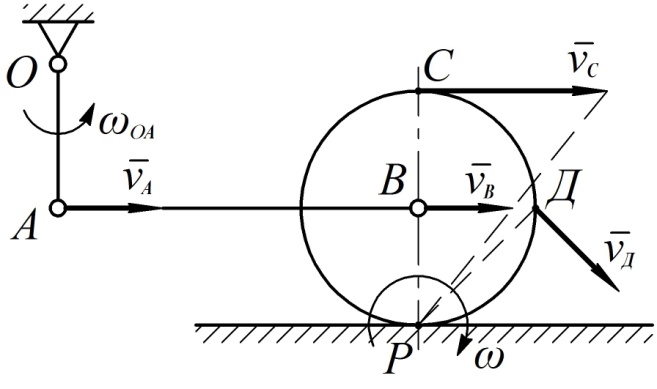 Рис. 41
Рис. 41
|
Вычислим вначале скорость точки 
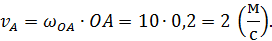
Покажем вектор 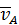 на рисунке, направив его перпендикулярно
на рисунке, направив его перпендикулярно  и согласовав по направлению с направлением угловой скорости
и согласовав по направлению с направлением угловой скорости 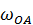 . Шатун совершает плоское движение. Построим для шатуна
. Шатун совершает плоское движение. Построим для шатуна 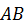 мгновенный центр скоростей. Проведем перпендикуляры к скоростям точек
мгновенный центр скоростей. Проведем перпендикуляры к скоростям точек  и
и  (при этом учтем, что скорость точки
(при этом учтем, что скорость точки  направлена горизонтально, так как траекторией этой точки является горизонтальная прямая). Проведенные перпендикуляры параллельны. Следовательно, мгновенный центр скоростей шатуна находится в бесконечности и скорости точек
направлена горизонтально, так как траекторией этой точки является горизонтальная прямая). Проведенные перпендикуляры параллельны. Следовательно, мгновенный центр скоростей шатуна находится в бесконечности и скорости точек  и
и  равны по величине
равны по величине
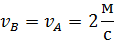
и одинаково направлены. Покажем вектор 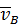 на рисунке. Так как диск катится без проскальзывания, то его МЦС находится в точке контакта с опорной поверхностью (точка
на рисунке. Так как диск катится без проскальзывания, то его МЦС находится в точке контакта с опорной поверхностью (точка  на рисунке). Найдем теперь угловую скорость диска
на рисунке). Найдем теперь угловую скорость диска
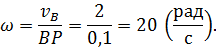
Покажем ее на рисунке, согласовав по направлению со скоростью точки  . Далее легко вычислить величины скоростей точек
. Далее легко вычислить величины скоростей точек  и
и 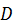 диска
диска
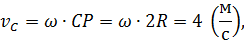
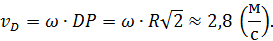
Покажем векторы  и
и 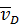 на рисунке, направив их перпендикулярно отрезкам
на рисунке, направив их перпендикулярно отрезкам 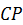 и
и 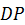 и согласовав по направлению с
и согласовав по направлению с 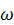 .
.
§ 4.4. Ускорения точек тела при плоском движении
Теорема сложения ускорений при плоском движении тела
Ускорение любой точки плоской фигуры может быть найдено как геометрическая сумма ускорения полюса и ускорения точки при ее относительном вращении вокруг подвижной оси, мысленно связанной с полюсом.
Доказательство
Рассмотрим движение точки 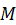 плоской фигуры как сложное, связав поступательно перемещающуюся подвижную систему координат с полюсом
плоской фигуры как сложное, связав поступательно перемещающуюся подвижную систему координат с полюсом  . Тогда ускорение точки
. Тогда ускорение точки 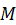 можно найти по теореме Кориолиса:
можно найти по теореме Кориолиса:
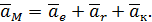
| (50) |
Так как переносное движение является поступательным вместе с полюсом  , то переносное ускорение
, то переносное ускорение

и переносная угловая скорость 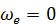 . Поэтому ускорение Кориолиса
. Поэтому ускорение Кориолиса
 Рис. 42
Рис. 42
|
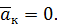
Относительное ускорение точки при относительном вращении вокруг полюса  обозначим
обозначим
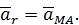
Тогда формула (50) примет вид
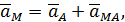
| (51) |
что и доказывает теорему.
Поясним более подробно векторное равенство (51). Ускорение при относительном вращении вокруг полюса состоит из нормальной и тангенциальной составляющих (см. рис. 42)
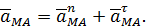
Поэтому более подробно векторное равенство (51) можно записать в виде
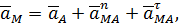
| (52) |
Причем
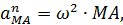
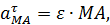

Отметим, что полное относительное ускорение 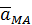 составляет с отрезком
составляет с отрезком 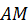 угол
угол 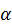 , тангенс которого можно определить по формуле (см. рис. 42)
, тангенс которого можно определить по формуле (см. рис. 42)
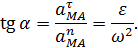
| (53) |
Из формулы (53) следует, что угол 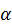 для всех точек плоской фигуры одинаков. От ускорения
для всех точек плоской фигуры одинаков. От ускорения 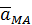 к отрезку
к отрезку 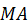 его надо откладывать в направлении углового ускорения
его надо откладывать в направлении углового ускорения 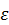 .
.
Таким образом, с помощью формулы (52) можно вычислить ускорение любой точки плоской фигуры, если известны ускорение полюса  , угловая скорость
, угловая скорость 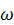 и угловое ускорение
и угловое ускорение 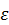 .
.
§ 4.5. Мгновенный центр ускорений
Теорема о существовании мгновенного центра ускорений
В любой момент времени при плоском движении фигуры в ее плоскости, если 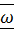 и
и 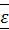 не равны нулю одновременно, существует единственная точка подвижной плоскости, мысленно связанной с фигурой, ускорение которой равно нулю. Эту точку называют мгновенным центром ускорений (МЦУ).
не равны нулю одновременно, существует единственная точка подвижной плоскости, мысленно связанной с фигурой, ускорение которой равно нулю. Эту точку называют мгновенным центром ускорений (МЦУ).
Доказательство
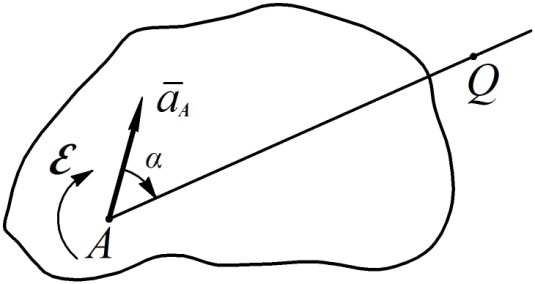 Рис. 43
Рис. 43
|
 , ее угловая скорость
, ее угловая скорость 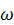 и угловое ускорение
и угловое ускорение 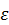 (см. рис. 43).
(см. рис. 43).
Вычислим угол 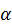 по формуле
по формуле
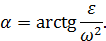
Мысленно повернем вектор  на угол
на угол 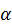 в сторону
в сторону 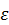 и проведем из точки
и проведем из точки  луч в полученном направлении. Отложим на этом луче расстояние
луч в полученном направлении. Отложим на этом луче расстояние 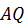 , вычисленное по формуле
, вычисленное по формуле
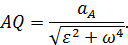
Найдем далее ускорение точки 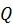 по теореме сложения ускорений, выбрав в качестве полюса точку
по теореме сложения ускорений, выбрав в качестве полюса точку  ,
,

Величина ускорения точки 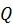 при ее относительном вращении вокруг полюса
при ее относительном вращении вокруг полюса  равна
равна
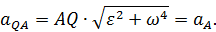
Вектор  будет направлен под углом
будет направлен под углом 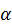 к отрезку
к отрезку 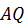 , как показано на рис. 43. Поэтому
, как показано на рис. 43. Поэтому 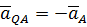 и для ускорения точки
и для ускорения точки 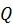 имеем
имеем
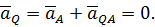
Следовательно, точка 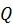 является мгновенным центром ускорений. Теорема доказана.
является мгновенным центром ускорений. Теорема доказана.
Если мгновенный центр ускорений выбрать в качестве полюса, то для ускорения точки  плоской фигуры из (51) получим
плоской фигуры из (51) получим
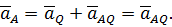
Для модуля ускорения точки  имеем
имеем
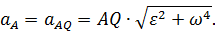
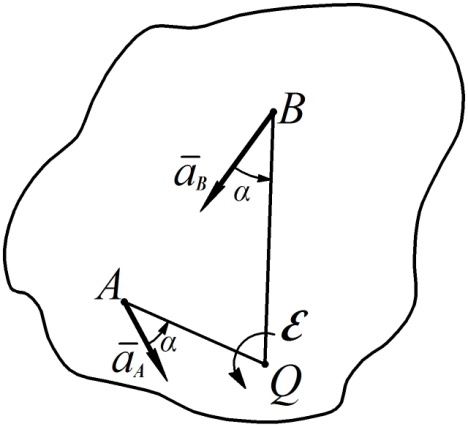 Рис. 44
Рис. 44
|
 направлен под углом
направлен под углом 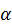 к отрезку
к отрезку 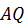 , причем поворот от вектора
, причем поворот от вектора  к отрезку
к отрезку 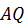 на угол
на угол 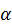 осуществляется в направлении углового ускорения
осуществляется в направлении углового ускорения 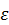 (см. рис. 44).
(см. рис. 44).
Аналогично для точки 

и ускорение 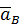 также направлено под углом
также направлено под углом 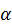 к отрезку
к отрезку 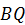 .
.
Из двух последних формул следует, что

т.е. ускорения точек плоской фигуры при плоском движении пропорциональны расстояниям от этих точек до мгновенного центра ускорений.
Обобщая полученные результаты, можно сделать вывод, что
ускорения точек плоской фигуры при плоском движении можно находить так же, как и при ее вращательном движении вокруг мгновенного центра ускорений.
Пример 7
В кривошипно-шатунном механизме даны длина кривошипа 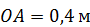 , длина шатуна
, длина шатуна 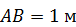 и постоянная угловая скорость вращения кривошипа
и постоянная угловая скорость вращения кривошипа 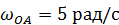 . Для заданного положения механизма, когда кривошип составляет с вертикалью угол
. Для заданного положения механизма, когда кривошип составляет с вертикалью угол 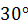 и шатун перпендикулярен кривошипу (см. рис. 45), найти ускорение поршня
и шатун перпендикулярен кривошипу (см. рис. 45), найти ускорение поршня  , а также положение МЦУ для шатуна
, а также положение МЦУ для шатуна 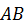 .
.
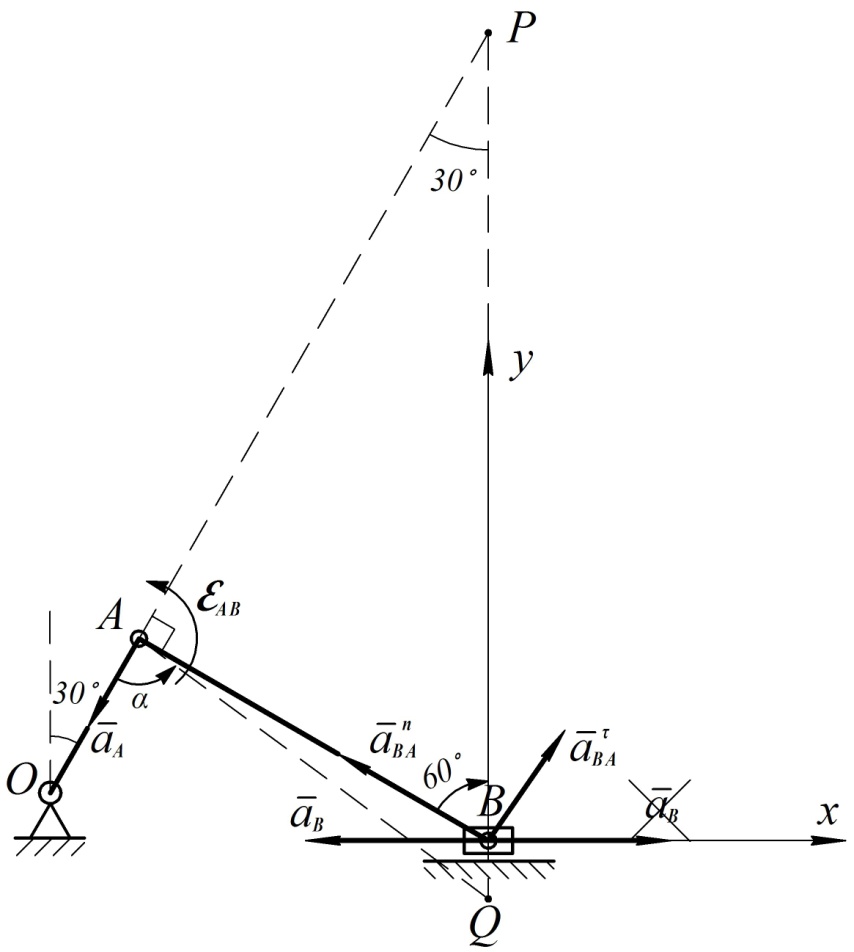 Рис. 45
Рис. 45
|
Решение
Найдем сначала ускорение точки  . Так как кривошип
. Так как кривошип  вращается с постоянной угловой скоростью, то
вращается с постоянной угловой скоростью, то
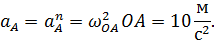
Изобразим вектор  на рис. 45, направив его к оси вращения. Выбрав точку
на рис. 45, направив его к оси вращения. Выбрав точку  в качестве полюса, ускорение точки
в качестве полюса, ускорение точки  можно найти по теореме сложения ускорений (формула (52))
можно найти по теореме сложения ускорений (формула (52))
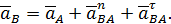
| (54) |
Нормальное ускорение точки  при ее относительном вращении вокруг полюса
при ее относительном вращении вокруг полюса  равно:
равно:
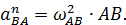
Для нахождения угловой скорости 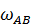 построим мгновенный центр скоростей для шатуна
построим мгновенный центр скоростей для шатуна 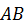 (точка
(точка  на рис. 45), восстановив перпендикуляры к направлениям скоростей точек
на рис. 45), восстановив перпендикуляры к направлениям скоростей точек  и
и  . После этого можем вычислить
. После этого можем вычислить
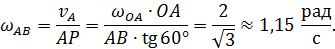
Теперь можно найти
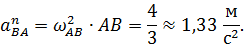
Вектор 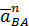 направим от точки
направим от точки  к полюсу
к полюсу  .
.
Для двух оставшихся векторов в равенстве (54) известны линии действия. Вектор 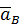 направлен по горизонтали вдоль траектории точки
направлен по горизонтали вдоль траектории точки  . Вектор
. Вектор 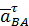 направлен перпендикулярно шатуну
направлен перпендикулярно шатуну 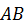 по касательной к относительной траектории точки
по касательной к относительной траектории точки  . Точное направление этих векторов неизвестно, поэтому направим их вдоль указанных линий действия наугад: вектор
. Точное направление этих векторов неизвестно, поэтому направим их вдоль указанных линий действия наугад: вектор 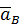 – по горизонтали вправо, вектор
– по горизонтали вправо, вектор 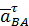 – перпендикулярно
– перпендикулярно 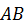 вверх (см. рис. 45). Выберем оси координат и векторное равенство (54) в проекциях на эти оси:
вверх (см. рис. 45). Выберем оси координат и векторное равенство (54) в проекциях на эти оси:

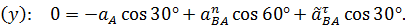
Так как направления векторов 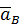 и
и 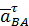 выбраны наугад, то в записанных формулах их модули заменены соответствующими алгебраическими значениями
выбраны наугад, то в записанных формулах их модули заменены соответствующими алгебраическими значениями 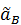 и
и 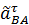 , которые могут быть как положительными, так и отрицательными величинами. Решая эту систему уравнений, найдем
, которые могут быть как положительными, так и отрицательными величинами. Решая эту систему уравнений, найдем

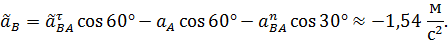
Полученные результаты показывают, что вектор 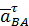 направлен на рис. 45 верно, а направление вектора
направлен на рис. 45 верно, а направление вектора 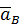 следует изменить на противоположное. Для модулей этих векторов имеем
следует изменить на противоположное. Для модулей этих векторов имеем
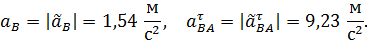
Построим теперь МЦУ для шатуна 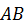 . Вычислим сначала угловое ускорение
. Вычислим сначала угловое ускорение
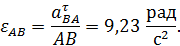
Изобразим 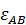 на рис. 45 в виде дуговой стрелки, согласованной с направлением вектора
на рис. 45 в виде дуговой стрелки, согласованной с направлением вектора 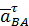 . Найдем далее угол
. Найдем далее угол
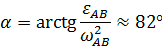
и расстояние 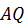 от точки
от точки  до МЦУ
до МЦУ
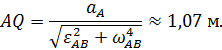
Построим теперь точку 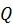 на рис. 45, повернув вектор
на рис. 45, повернув вектор  на угол
на угол 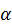 в направлении
в направлении 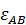 и отложив на полученном луче расстояние
и отложив на полученном луче расстояние 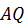 .
.
Если теперь соединить МЦУ с точкой  , то вектор
, то вектор 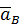 должен составлять с отрезком
должен составлять с отрезком 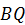 такой же угол
такой же угол 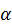 ускорения точек
ускорения точек  и
и  должны быть пропорциональны расстояниям от точек до МЦУ
должны быть пропорциональны расстояниям от точек до МЦУ
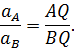
§ 4.6. Вычисление угловой скорости и углового ускорения тела при плоском движении
Как видно из выше изложенного, при вычислении скоростей и ускорений точек тела при плоском движении важно уметь найти угловую скорость и угловое ускорение тела. Остановимся на этом отдельно.
Основные способы вычисления угловой скорости
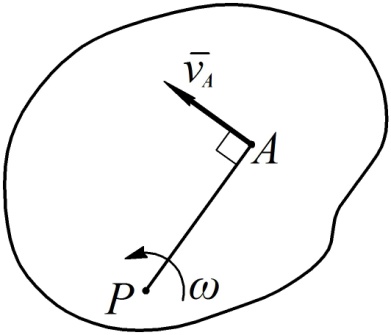 Рис. 46
Рис. 46
|
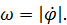
2. Если известны скорость какой-либо точки тела и положение МЦС, то угловая скорость может быть найдена по формуле (48)
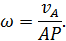
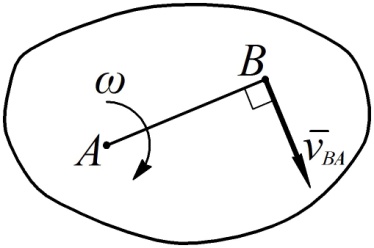 Рис. 47
Рис. 47
|
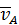 (см. рис. 46).
(см. рис. 46).
3. Угловая скорость может быть также найдена, если известна скорость при относительном вращении какой-либо точки  вокруг полюса
вокруг полюса  . В этом случае
. В этом случае
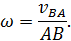
Направление угловой скорости здесь должно быть согласовано с направлением вектора относительной скорости 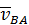 (см. рис. 47).
(см. рис. 47).
Основные способы вычисления углового ускорения
1. Если заданы кинематические уравнения движения тела (41), то угловое ускорение найдется согласно определению

2. Если угловая скорость была найдена по формуле (48)
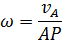
и расстояние от точки  до мгновенного центра скоростей не изменяется при движении тела (
до мгновенного центра скоростей не изменяется при движении тела ( 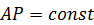 ), то, дифференцируя по времени последнее выражение для углового ускорения, получим
), то, дифференцируя по времени последнее выражение для углового ускорения, получим
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|