
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пример 10 3 страница
Каждый из входящих в равенство (34) векторов должен быть направлен по касательной к соответствующей траектории. Геометрическая интерпретация доказанной теоремы представлена на рис. 22.
Рассмотрим пример решения задачи.
Пример 4
По грани призмы, движущейся влево со скоростью  , скользит конец
, скользит конец  стержня
стержня 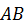 (рис. 23). Задан угол
(рис. 23). Задан угол 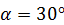 . Найти скорость скольжения точки
. Найти скорость скольжения точки  относительно призмы.
относительно призмы.
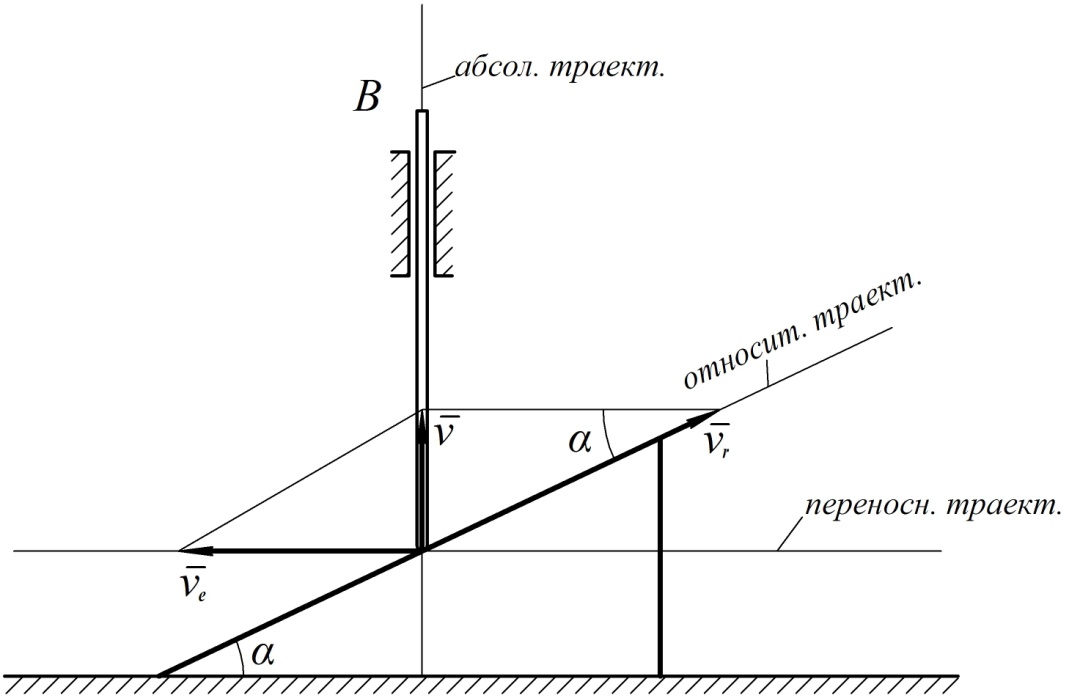 Рис. 23
Рис. 23
|
Решение
Рассмотрим движение точки  как сложное. Свяжем подвижную систему координат с призмой. Проведем через точку
как сложное. Свяжем подвижную систему координат с призмой. Проведем через точку  относительную, переносную и абсолютную траектории. Учитывая, что переносная скорость
относительную, переносную и абсолютную траектории. Учитывая, что переносная скорость 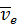 (заданная скорость призмы) направлена влево, построим параллелограмм, соответствующий векторному равенству:
(заданная скорость призмы) направлена влево, построим параллелограмм, соответствующий векторному равенству:
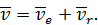
Из рисунка следует, что
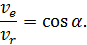
Отсюда находим искомую относительную скорость
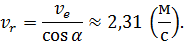
§ 3.4. Теорема сложения ускорений при сложном движении точки
Эта теорема устанавливает связь между абсолютным, относительным и переносным ускорениями точки при сложном движении. Ее называют теоремой Кориолиса по имени доказавшего ее французского ученого.
Теорема Кориолиса
Абсолютное ускорение точки при сложном движении равно геометрической сумме относительного, переносного и кориолисова ускорений.
Доказательство
Запишем полученную при доказательстве теоремы сложения скоростей формулу (33) в виде:
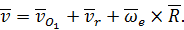
Вычислив полную производную по времени от обеих частей этого равенства, получим
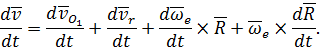
| (35) |
В этой формуле полная производная от абсолютной скорости равна абсолютному ускорению
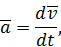
а полные производные от векторов 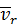 и
и 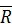 , заданных в подвижной системе координат, следует вычислить по формуле Бура:
, заданных в подвижной системе координат, следует вычислить по формуле Бура:

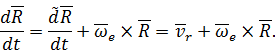
Тогда выражение (35) перепишется в виде
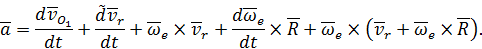
Учитывая, что локальная производная от относительной скорости равна относительному ускорению
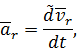
раскрывая скобки и приводя подобные члены из последнего выражения получим
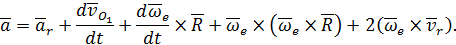
| (36) |
Если мысленно остановить относительное движение, положив 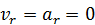 , то из формулы (36) получим выражение для переносного ускорения:
, то из формулы (36) получим выражение для переносного ускорения:
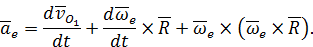
После этого выражение (36) можно переписать в виде
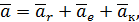
| (37) |
где

| (38) |
ускорение Кориолиса.
Теорема полностью доказана. Она выражается векторным равенством (37).
Поясним далее физический смысл и методы вычисления векторов в правой части равенства (37).
Относительное ускорение характеризует изменение вектора относительной скорости за счет относительного движения. Для его вычисления надо мысленно остановить переносное движение и представить себе, что точка движется по относительной траектории. В зависимости от вида относительной траектории относительное ускорение может иметь одну или две составляющих (см. рис. 24).
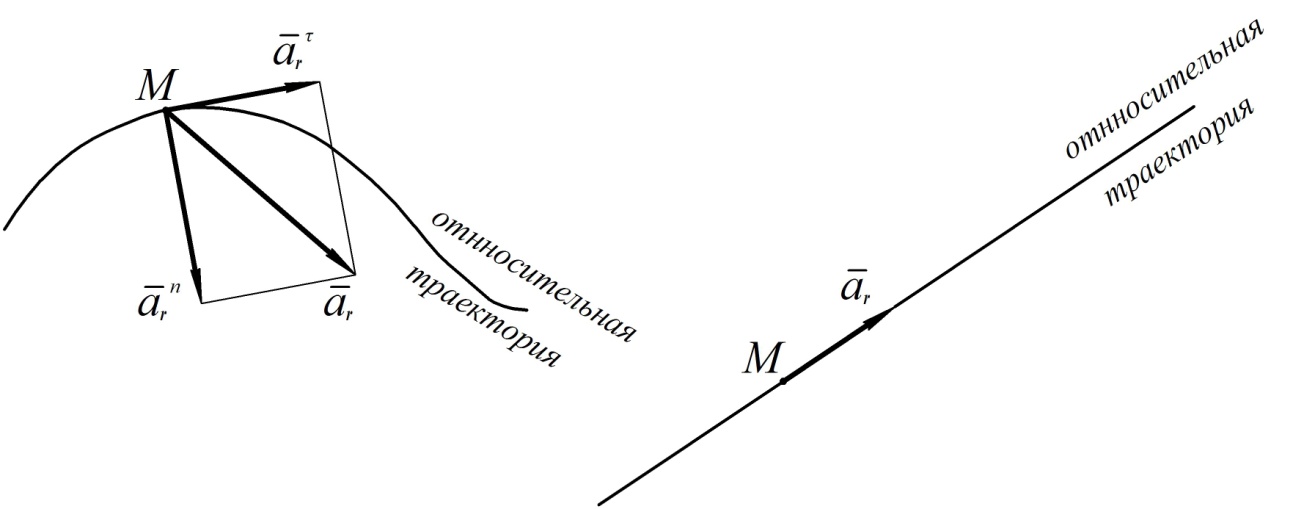 Рис. 24
Рис. 24
|
Переносное ускорение характеризует изменение вектора переносной скорости за счет переносного движения. Для его вычисления надо мысленно остановить относительное движение и представить себе, что точка движется по переносной траектории. В зависимости от вида переносной траектории переносное ускорение тоже может иметь одну или две составляющих (см. рис. 25).
Ускорение Кориолиса характеризует изменение вектора относительной скорости за счет переносного движения, а также изменение вектора переносной скорости за счет относительного движения. В соответствии с формулой (38) величина кориолисова ускорения может быть вычислена как модуль векторного произведения:
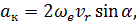
| (39) |
где 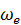 – модуль переносной угловой скорости (угловой скорости подвижной системы координат),
– модуль переносной угловой скорости (угловой скорости подвижной системы координат), 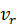 – модуль относительной скорости точки,
– модуль относительной скорости точки, 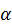 – угол между векторами
– угол между векторами 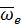 и
и 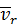 .
.
 Рис. 25
Рис. 25
|
Направление ускорения Кориолиса можно определить по правилу векторного произведения. Для этого нужно в рассматриваемой точке, совершающей сложное движение, построить векторы 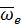 и
и 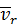 , провести перпендикуляр к плоскости указанных векторов и направить ускорение Кориолиса вдоль этого перпендикуляра по правилу правого винта, поворачивая винт в сторону кратчайшего совмещения вектора
, провести перпендикуляр к плоскости указанных векторов и направить ускорение Кориолиса вдоль этого перпендикуляра по правилу правого винта, поворачивая винт в сторону кратчайшего совмещения вектора 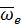 с вектором
с вектором 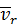 (см. рис. 26).
(см. рис. 26).
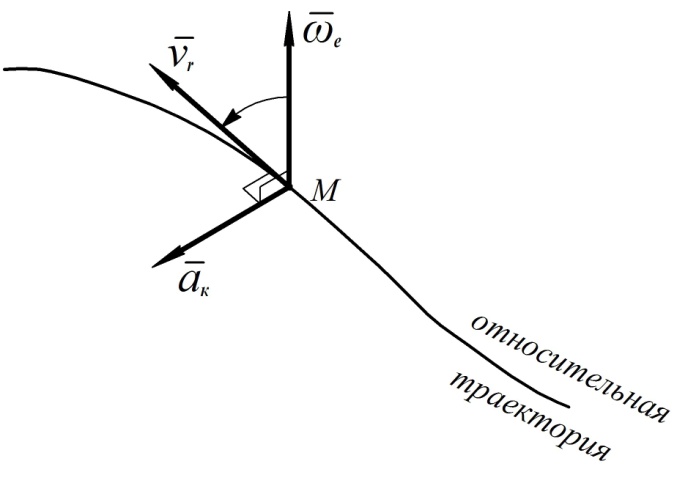 Рис. 26
Рис. 26
|
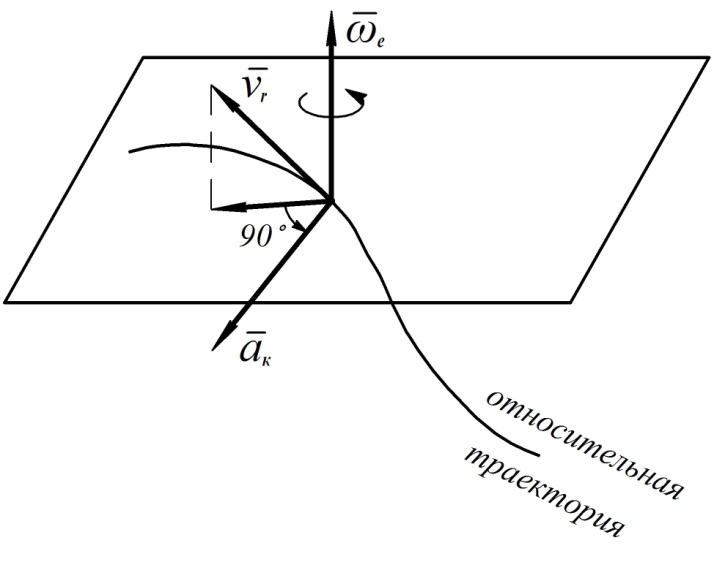 Рис. 27
Рис. 27
|
Направление ускорения Кориолиса можно также определить по правилу Жуковского. Для этого нужно спроецировать вектор 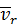 на плоскость, перпендикулярную вектору
на плоскость, перпендикулярную вектору 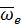 , и повернуть полученную проекцию в указанной плоскости на угол
, и повернуть полученную проекцию в указанной плоскости на угол 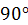 в направлении переносного вращения (см. рис. 27).
в направлении переносного вращения (см. рис. 27).
Отметим особо частные случаи, когда ускорение Кориолиса обращается в нуль:
1) при 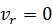 , т.е. в те моменты времени, когда относительная скорость равна нулю;
, т.е. в те моменты времени, когда относительная скорость равна нулю;
2) при 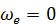 , т.е. если подвижная система координат движется поступательно;
, т.е. если подвижная система координат движется поступательно;
3) при 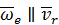 , т.е. если относительная скорость параллельна оси переносного вращения.
, т.е. если относительная скорость параллельна оси переносного вращения.
Пример 5
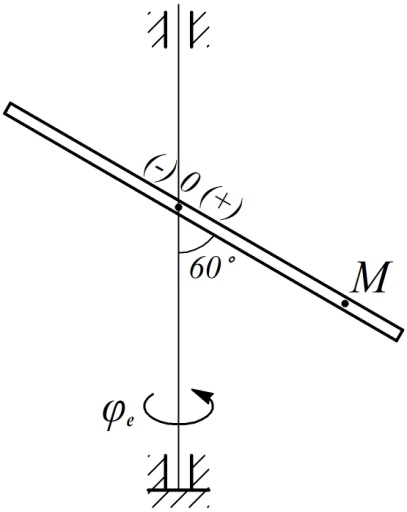 Рис. 28
Рис. 28
|
Прямолинейная трубка прикреплена к вертикальной оси под углом  и вращается вокруг нее по закону
и вращается вокруг нее по закону 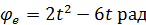 . Вдоль трубки по закону
. Вдоль трубки по закону 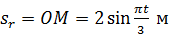 движется шарик
движется шарик 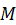 (см. рис. 28). Положительное направление отсчета угла
(см. рис. 28). Положительное направление отсчета угла 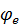 показано на рисунке дуговой стрелкой,
показано на рисунке дуговой стрелкой, 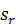 считается положительным вниз по трубке от точки
считается положительным вниз по трубке от точки  . Требуется определить величину абсолютного ускорения точки
. Требуется определить величину абсолютного ускорения точки 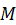 в момент времени
в момент времени 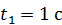 .
.
Решение
Мысленно свяжем подвижную систему координат с трубкой. Тогда переносным движением будет вращение трубки вокруг вертикальной оси, а относительным движением будет прямолинейное движение шарика вдоль трубки.
Определим сначала положение шарика в трубке в момент 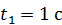 . Для этого вычислим
. Для этого вычислим
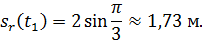
Отложим полученное расстояние от точки  в положительном направлении отсчета
в положительном направлении отсчета 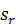 . Проведем через найденное положение шарика относительную и переносную траектории (см. рис. 29).
. Проведем через найденное положение шарика относительную и переносную траектории (см. рис. 29).
Запишем теперь выражение для абсолютного ускорения точки М в соответствии с теоремой сложения ускорений:
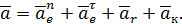
| (40) |
В связи с тем, что переносная траектория окружность, переносное ускорение здесь разложено на нормальную и тангенциальную составляющие. Вычислим далее величину каждого из векторов в правой части выражения (40) для момента времени 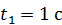 и изобразим эти векторы на рис. 29.
и изобразим эти векторы на рис. 29.
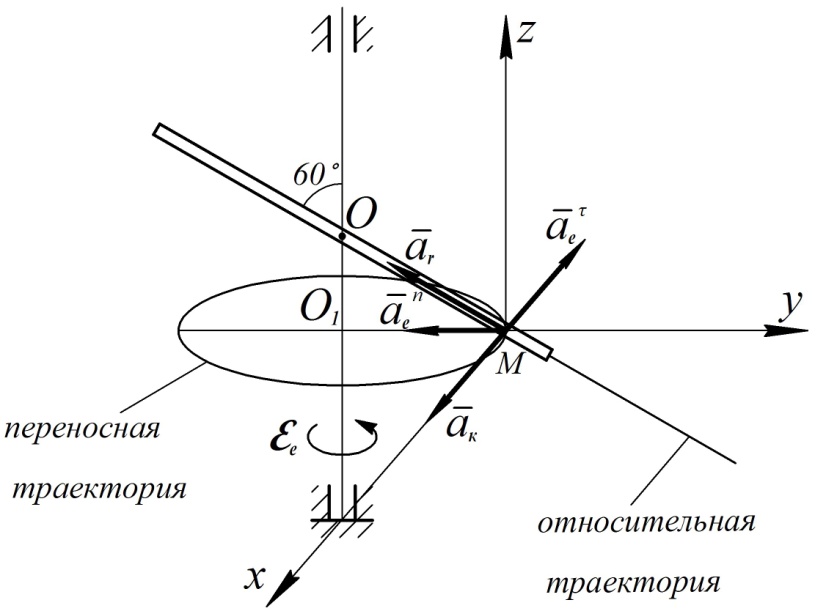 Рис. 29
Рис. 29
|
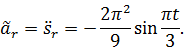
В момент времени 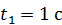
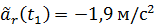 . Следовательно, для величины относительного ускорения имеем
. Следовательно, для величины относительного ускорения имеем 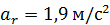 . Знак алгебраического значения показывает, что вектор
. Знак алгебраического значения показывает, что вектор 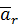 направлен в сторону отрицательных значений
направлен в сторону отрицательных значений 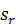 . Изобразим вектор
. Изобразим вектор 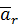 на рис. 29.
на рис. 29.
Вычислим теперь для момента времени 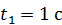 составляющие переносного ускорения:
составляющие переносного ускорения:


Здесь
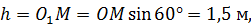
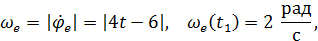

Покажем на рис. 29 вектор  , направив его к центру кривизны переносной траектории. Так как
, направив его к центру кривизны переносной траектории. Так как  , то переносное угловое ускорение
, то переносное угловое ускорение 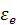 будет направлено в сторону положительного направления отсчета угла
будет направлено в сторону положительного направления отсчета угла 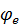 и вектор
и вектор 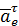 следует направить по касательной к переносной траектории в направлении
следует направить по касательной к переносной траектории в направлении 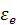 (см. рис. 29).
(см. рис. 29).
Определим теперь величину и направление ускорения Кориолиса для момента времени 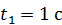 . Для этого момента времени алгебраическое значение переносной угловой скорости будет равно
. Для этого момента времени алгебраическое значение переносной угловой скорости будет равно
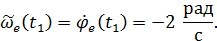
Поэтому угловая переносная скорость будет направлена в сторону отрицательных значений угла 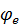 и вектор
и вектор 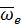 будет направлен вниз вдоль оси переносного вращения (см. рис. 30). Алгебраическое значение относительной скорости для момента времени
будет направлен вниз вдоль оси переносного вращения (см. рис. 30). Алгебраическое значение относительной скорости для момента времени 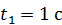
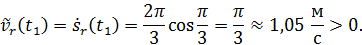
 Рис. 30
Рис. 30
|
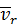 направлен вдоль относительной траектории в сторону положительных значений
направлен вдоль относительной траектории в сторону положительных значений 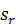 . Для модуля ускорения Кориолиса получим
. Для модуля ускорения Кориолиса получим
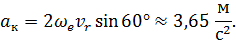
В соответствии с правилом векторного произведения вектор 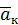 будет направлен перпендикулярно плоскости рисунка вдоль оси
будет направлен перпендикулярно плоскости рисунка вдоль оси 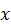 . Покажем этот вектор на рис. 29 и 30.
. Покажем этот вектор на рис. 29 и 30.
Для нахождения абсолютного ускорения точки выберем в точке 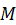 оси декартовой системы координат и запишем векторное равенство (40) в проекциях на эти оси:
оси декартовой системы координат и запишем векторное равенство (40) в проекциях на эти оси:
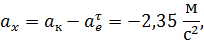
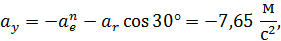

Через найденные проекции величину абсолютного ускорения вычислим по формуле
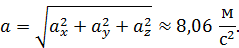
Глава 4. Плоское движение твердого тела
§ 4.1. Основные понятия
Плоским (плоскопараллельным) называется такое движение твердого тела, при котором каждая его точка все время движется в одной и той же плоскости.
Плоскости, в которых движутся различные точки тела, параллельны между собой и параллельны одной и той же неподвижной плоскости. Траектории точек тела при этом являются плоскими кривыми. Плоское движение твердого тела имеет большое значение в технике, так как это движение совершают большинство звеньев в механизмах и машинах. Вращательное движение твердого тела можно считать частным случаем плоского.
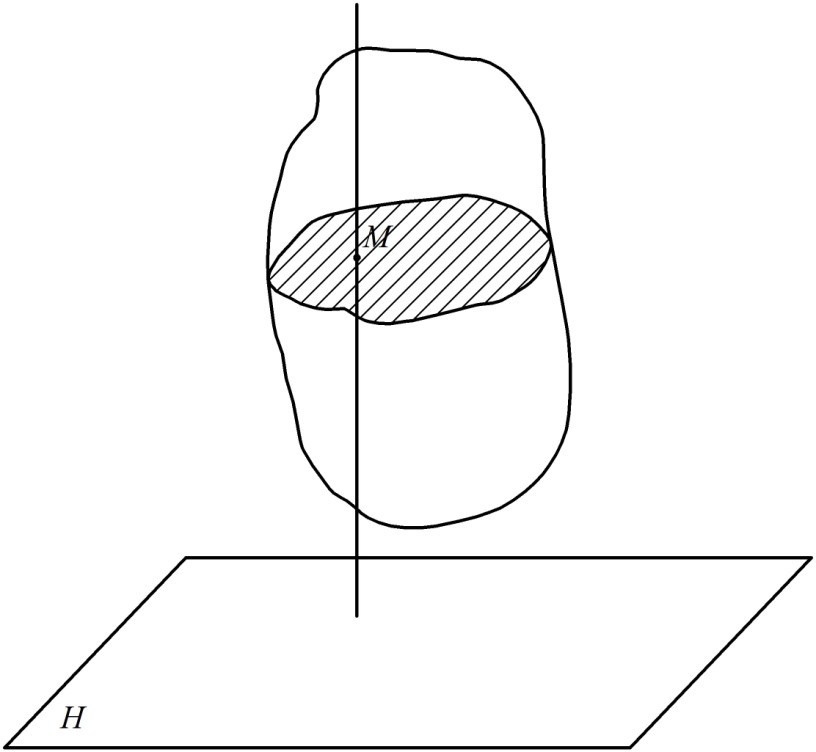 Рис. 31
Рис. 31
|
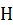 (см. рис. 31).
(см. рис. 31).
Тогда любая прямая, перпендикулярная к этой плоскости и жестко связанная с телом, будет двигаться поступательно. То есть, все точки этой прямой движутся одинаково. Достаточно изучить движение одной из них, например, точки 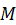 . Рассуждая аналогично для точек тела, лежащих на других скрепленных с телом прямых, перпендикулярных плоскости
. Рассуждая аналогично для точек тела, лежащих на других скрепленных с телом прямых, перпендикулярных плоскости 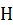 , можно сделать вывод, что для изучения плоского движения твердого тела достаточно изучить движение только одного его сечения плоскостью, параллельной плоскости
, можно сделать вывод, что для изучения плоского движения твердого тела достаточно изучить движение только одного его сечения плоскостью, параллельной плоскости 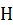 . Это сечение в дальнейшем будем называть плоской фигурой и располагать в плоскости чертежа.
. Это сечение в дальнейшем будем называть плоской фигурой и располагать в плоскости чертежа.
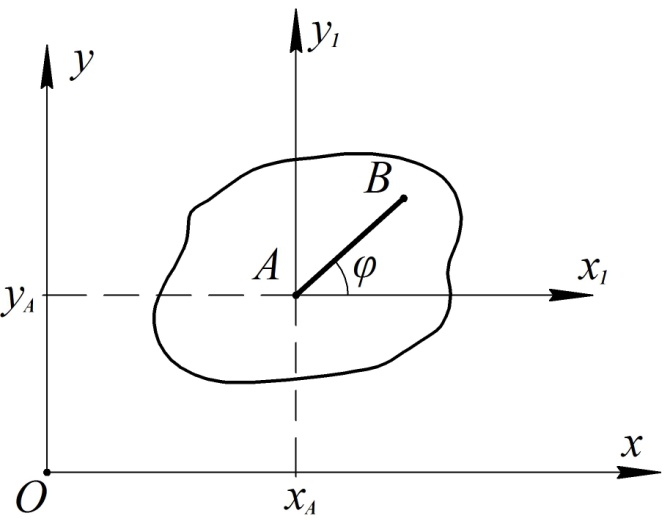 Рис. 32
Рис. 32
|
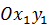 свяжем с неподвижной плоскостью
свяжем с неподвижной плоскостью 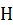 (плоскостью рисунка), а поступательно перемещающуюся подвижную систему координат
(плоскостью рисунка), а поступательно перемещающуюся подвижную систему координат  свяжем с выбранной точкой
свяжем с выбранной точкой  плоской фигуры, называемой полюсом (см. рис. 32).
плоской фигуры, называемой полюсом (см. рис. 32).
Тогда плоское движение фигуры разложится на поступательное переносное вместе с выбранной подвижной системой координат и относительное вращательное по отношению к подвижной оси 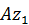 , проходящей через полюс
, проходящей через полюс  и перпендикулярной плоскости рисунка. Для характеристики вращательной части плоского движения относительно указанной выше подвижной оси вводится понятие угловой скорости и углового ускорения тела при плоском движении.
и перпендикулярной плоскости рисунка. Для характеристики вращательной части плоского движения относительно указанной выше подвижной оси вводится понятие угловой скорости и углового ускорения тела при плоском движении.
Если на плоской фигуре выбрать еще точку  , провести отрезок
, провести отрезок 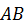 и задать координаты полюса и угол
и задать координаты полюса и угол 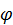 (см. рис. 32) как функции времени
(см. рис. 32) как функции времени
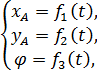
| (41) |
то записанные уравнения (41) называют кинематическими уравнениями плоского движения тела.
Докажем далее теорему о перемещении плоской фигуры.
Теорема
Плоскую фигуру из одного ее положения в любое другое можно перевести двумя перемещениями – поступательным в плоскости фигуры вместе с выбранным полюсом и поворотом в этой же плоскости вокруг этого полюса. При этом поступательная часть перемещения зависит от выбора полюса, а вращательная часть перемещения не зависит от выбора полюса.
Доказательство
Рассмотрим два любых положения плоской фигуры в ее плоскости, определяемые двумя положениями отрезка 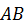 , скрепленного с этой фигурой (см. рис. 33).
, скрепленного с этой фигурой (см. рис. 33).
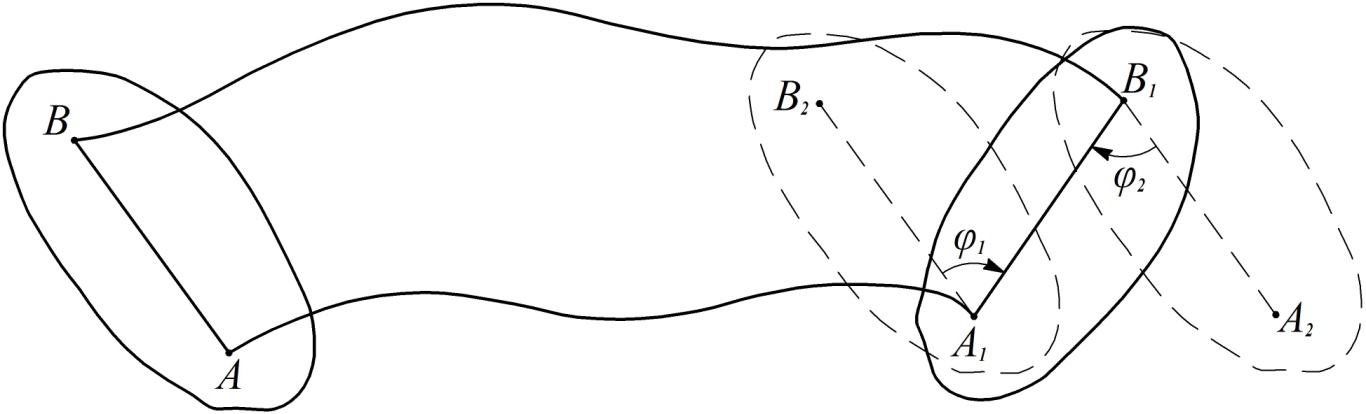 Рис. 33
Рис. 33
|
Переместим плоскую фигуру из левого положения в правое сначала поступательно вместе с точкой  , причем скрепленный с ней отрезок
, причем скрепленный с ней отрезок 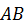 останется параллельным своему первоначальному положению и займет положение
останется параллельным своему первоначальному положению и займет положение  , а затем повернем фигуру вокруг точки
, а затем повернем фигуру вокруг точки  на угол
на угол 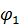 до совпадения
до совпадения  с
с 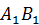 .
.
Далее, выбрав в качестве полюса точку  , переместим фигуру сначала поступательно вместе с точкой
, переместим фигуру сначала поступательно вместе с точкой  . При этом отрезок
. При этом отрезок 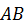 займет положение
займет положение 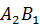 . После этого повернем фигуру на угол
. После этого повернем фигуру на угол  вокруг точки
вокруг точки  до совпадения
до совпадения 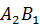 с
с 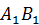 . Из рисунка видно, что поступательная часть перемещения зависит от выбора полюса (определяется траекторией полюса), а вращательная часть перемещения не зависит от выбора полюса, так как
. Из рисунка видно, что поступательная часть перемещения зависит от выбора полюса (определяется траекторией полюса), а вращательная часть перемещения не зависит от выбора полюса, так как 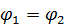 как накрестлежащие углы и направление поворота вокруг выбранных полюсов тоже одинаково. Выбирая различные полюсы такое перемещение плоской фигуры можно производить бесчисленным количеством способов. Теорема доказана.
как накрестлежащие углы и направление поворота вокруг выбранных полюсов тоже одинаково. Выбирая различные полюсы такое перемещение плоской фигуры можно производить бесчисленным количеством способов. Теорема доказана.
Из доказанной теоремы следует, что угловая скорость и угловое ускорение тела при плоском движении не завися от выбора полюса, то есть, в любой момент времени плоская фигура относительно подвижных осей, мысленно скрепленных с различными полюсами, поворачивается с одинаковыми угловыми скоростями и одинаковыми угловыми ускорениями.
§ 4.2. Скорости точек тела при плоском движении
В данном параграфе рассмотрим способы вычисления скоростей точек тела при плоском движении. Эти способы основаны на двух доказываемых ниже теоремах.
Теорема сложения скоростей при плоском движении тела
Скорость любой точки плоской фигуры может быть вычислена как геометрическая сумма скорости полюса и скорости точки при ее относительном вращении вокруг подвижной оси, связанной с полюсом.
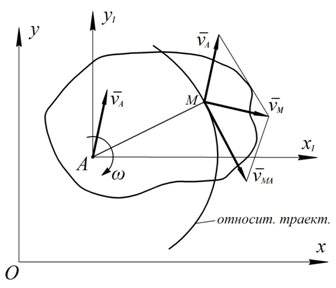 Рис. 34
Рис. 34
|
Рассмотрим движение точки 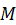 плоской фигуры как сложное, связав поступательно перемещающуюся подвижную систему координат с полюсом
плоской фигуры как сложное, связав поступательно перемещающуюся подвижную систему координат с полюсом  (см. рис. 34).
(см. рис. 34).
Тогда по теореме сложения скоростей при сложном движении точки имеем
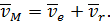
| (42) |
Так как подвижная система координат движется поступательно, то переносная скорость точки равна скорости полюса 

Относительным движением является вращение вокруг подвижной оси 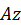 . Обозначим относительную скорость
. Обозначим относительную скорость 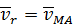 . Она направлена по касательной к относительной траектории (перпендикулярно отрезку
. Она направлена по касательной к относительной траектории (перпендикулярно отрезку 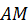 ), согласуясь по направлению с угловой скоростью
), согласуясь по направлению с угловой скоростью 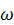 (см. рис. 34). Величина относительной скорости в данном случае может быть найдена по формуле для вращательного движения
(см. рис. 34). Величина относительной скорости в данном случае может быть найдена по формуле для вращательного движения
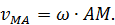
После этого выражение (42) можно записать в окончательном виде
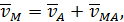
| (43) |
выражающем доказываемую теорему.
С помощью доказанной теоремы можно определить скорость любой точки тела, если известны скорость полюса и угловая скорость тела. Еще одна теорема, позволяющая находить скорости точек тела при плоском движении, вытекает из предыдущей.
Теорема о проекциях скоростей точек тела
При плоском движении тела проекции скоростей двух любых его точек на ось, проведенную через эти точки, равны.
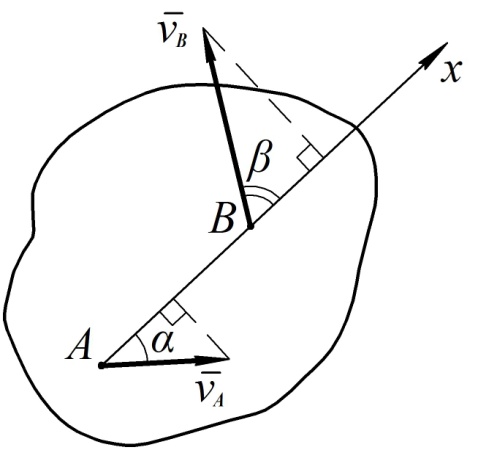 Рис. 35
Рис. 35
|
Для доказательства выберем на теле две произвольные точки  и
и  и проведем через эти точки ось
и проведем через эти точки ось 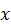 (см. рис. 35).
(см. рис. 35).
Запишем в соответствии с (43) выражение для скорости точки  , выбрав в качестве полюса точку
, выбрав в качестве полюса точку 
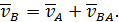
| (44) |
Запишем теперь векторное равенство (44) в проекциях на ось 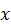
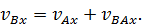
Учитывая, что вектор 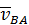 перпендикулярен отрезку
перпендикулярен отрезку 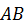 (
( 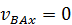 ), получим отсюда утверждение теоремы
), получим отсюда утверждение теоремы
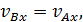
| (45) |
которое еще можно переписать в виде (см. рис. 35)
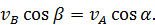
§ 4.3. Мгновенный центр скоростей
Теорема о существовании мгновенного центра скоростей
В любой момент времени при плоском движении фигуры в ее плоскости, если 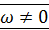 , существует единственная точка подвижной плоскости, мысленно связанной с фигурой, скорость которой равна нулю. Эта точка называется мгновенным центром скоростей (МЦС).
, существует единственная точка подвижной плоскости, мысленно связанной с фигурой, скорость которой равна нулю. Эта точка называется мгновенным центром скоростей (МЦС).
Доказательство
 Рис. 36
Рис. 36
|
 плоской фигуры
плоской фигуры 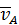 и угловая скорость
и угловая скорость 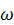 (см. рис. 36). Проведем из точки
(см. рис. 36). Проведем из точки  луч, повернув вектор скорости на угол
луч, повернув вектор скорости на угол 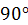 в направлении
в направлении 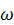 . Отложим на этом луче отрезок
. Отложим на этом луче отрезок  длиной
длиной
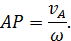
Вычислим теперь скорость точки  по теореме сложения скоростей
по теореме сложения скоростей
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|