
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пример 10 2 страница
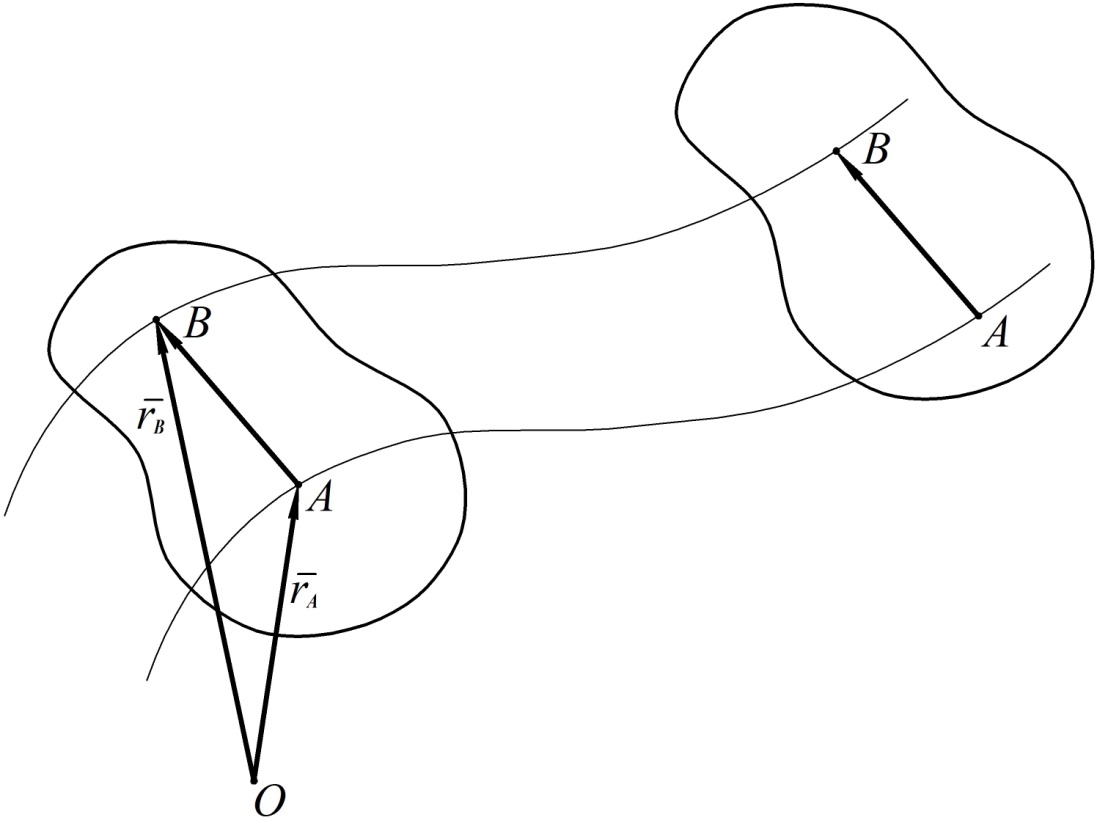 Рис. 11
Рис. 11
|
Из теоремы следует, что для изучения поступательного движения твердого тела достаточно изучить движение только одной его точки.
§ 2.2. Вращательное движение твердого тела
2.2.1. Основные понятия
 Рис. 12
Рис. 12
|
Прямая, проходящая через эти неподвижные точки, называется осью вращения. При вращательном движении точки тела, не лежащие на оси вращения, движутся по окружностям, расположенным в плоскостях, перпендикулярных к оси вращения с центрами на этой оси. Скорости точек, расположенных на оси вращения, равны нулю. На оси вращения обычно выбирают положительное направление (ось 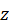 , рис. 12).
, рис. 12).
Проведем через ось вращения две полуплоскости: неподвижную 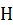 и неизменно связанную с телом
и неизменно связанную с телом 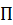 . Положение полуплоскости
. Положение полуплоскости 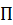 , а следовательно, и всего тела, можно задать линейным углом
, а следовательно, и всего тела, можно задать линейным углом 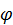 двугранного угла между полуплоскостями
двугранного угла между полуплоскостями 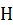 и
и 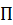 (рис. 12). Угол
(рис. 12). Угол 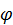 считается положительным, если он отсчитан от неподвижной плоскости к подвижной против часовой стрелки, если смотреть со стороны положительного направления оси вращения. Будучи отсчитанным по часовой стрелке, угол
считается положительным, если он отсчитан от неподвижной плоскости к подвижной против часовой стрелки, если смотреть со стороны положительного направления оси вращения. Будучи отсчитанным по часовой стрелке, угол 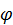 считается отрицательным.
считается отрицательным.
Введенный таким образом угол 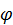 называется углом поворота тела. Если угол поворота задать как функцию времени, то полученное уравнение называют кинематическим уравнением вращательного движения твердого тела:
называется углом поворота тела. Если угол поворота задать как функцию времени, то полученное уравнение называют кинематическим уравнением вращательного движения твердого тела:
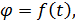
| (20) |
При изучении движения тела характеристики движения подразделяются на глобальные (одинаковые для всех точек тела) и локальные (различные для разных точек тела). Покажем далее, как с помощью уравнения (20) найти все эти характеристики движения.
2.2.2. Угловая скорость и угловое ускорение тела
Средней угловой скоростью тела за промежуток времени  называется
называется
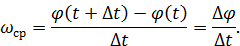
Мгновенной угловой скоростью (или просто угловой скоростью) тела в момент времени 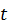 называется
называется
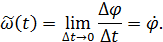
| (21) |
Определяемая по формуле (21) угловая скорость может принимать положительные и отрицательные значения. Поэтому величина 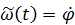 называется алгебраическим значением угловой скорости. Угловая скорость как физическая характеристика движения считается положительной и определяется выражением
называется алгебраическим значением угловой скорости. Угловая скорость как физическая характеристика движения считается положительной и определяется выражением

Угловая скорость характеризует быстроту вращения тела.
Аналогично определяются среднее и мгновенное угловые ускорения:

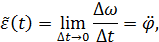
| (22) |
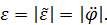
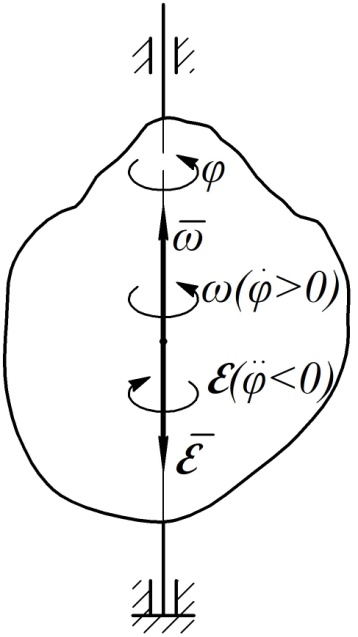 Рис. 13
Рис. 13
|
Иногда угловую скорость и угловое ускорение изображают в виде векторов, которые по модулю равны соответствующим физическим характеристикам и направлены вдоль оси вращения по правилу правого винта. Направив вдоль оси вращения ось 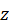 так, чтобы при взгляде навстречу этой оси положительное направление отсчета угла
так, чтобы при взгляде навстречу этой оси положительное направление отсчета угла 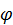 было видно против часовой стрелки, можно для введенных векторов написать соотношения
было видно против часовой стрелки, можно для введенных векторов написать соотношения
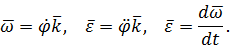
2.2.3. Простейшие случаи вращательного движения твердого тела
Отметим два важных простейших случая вращательного движения тела.
1. Равномерное вращение. Оно характеризуется постоянной угловой скоростью 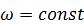 . В этом случае угловое ускорение
. В этом случае угловое ускорение 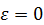 и угол поворота определяется по формуле
и угол поворота определяется по формуле
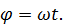
Здесь и далее считается, что начальному положению тела при 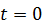 соответствует угол
соответствует угол 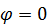 .
.
2. Равнопеременное вращение. Оно характеризуется постоянным угловым ускорением  . В этом случае угловая скорость и угол поворота тела рассчитываются по формулам
. В этом случае угловая скорость и угол поворота тела рассчитываются по формулам
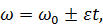
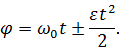
Здесь  – начальная угловая скорость, знак «
– начальная угловая скорость, знак « 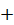 » соответствует равноускоренному вращению, знак «
» соответствует равноускоренному вращению, знак « 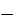 » – равнозамедленному.
» – равнозамедленному.
2.2.4. Определение скоростей и ускорений точек тела
Пусть задано кинематическое уравнение вращательного движения тела 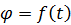 . Зададим движение произвольной точки
. Зададим движение произвольной точки 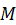 тела естественным способом. Начало отсчета дуговой координаты на траектории выберем в точке пересечения траектории с неподвижной полуплоскостью
тела естественным способом. Начало отсчета дуговой координаты на траектории выберем в точке пересечения траектории с неподвижной полуплоскостью 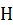 (см. рис. 14). Положительное направление отсчета дуговой координаты
(см. рис. 14). Положительное направление отсчета дуговой координаты  совместим с положительным направлением отсчета угла поворота
совместим с положительным направлением отсчета угла поворота 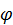 .
.
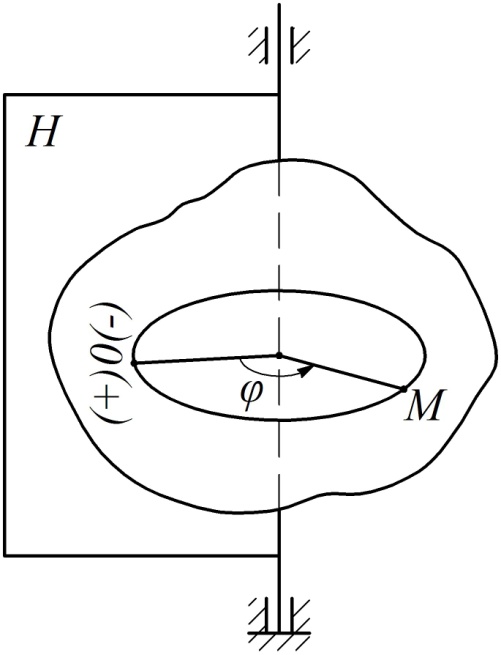 Рис. 14
Рис. 14
|
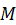 по ее траектории примет вид
по ее траектории примет вид
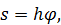
где 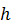 – расстояние от точки
– расстояние от точки 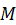 до оси вращения (радиус окружности, по которой движется точка).
до оси вращения (радиус окружности, по которой движется точка).
Для алгебраической скорости точки М получим

Модуль скорости точки определится по формуле
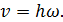
| (23) |
Вектор скорости  точки
точки 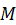 будет направлен по касательной к траектории, согласуясь с направлением угловой скорости.
будет направлен по касательной к траектории, согласуясь с направлением угловой скорости.
Тангенциальное и нормальное ускорения точки найдутся по формулам
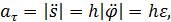
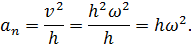
| (24) |
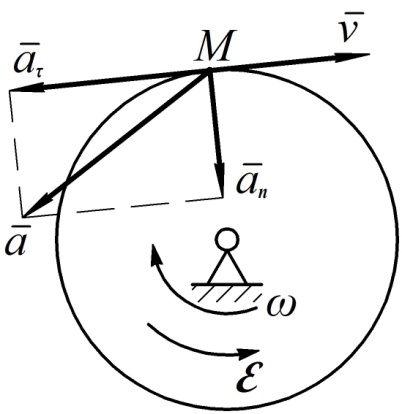 Рис. 15
Рис. 15
|
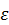 . Нормальное ускорение направлено перпендикулярно касательной к оси вращения. Полное ускорение найдется по теореме Пифагора
. Нормальное ускорение направлено перпендикулярно касательной к оси вращения. Полное ускорение найдется по теореме Пифагора
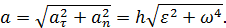
| (25) |
Направление векторов скорости и ускорения показано на рис. 15.
Найдем угол 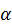 между векторами полного и нормального ускорения точки:
между векторами полного и нормального ускорения точки:
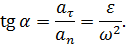
Из этой формулы следует, что угол a для всех точек тела в любой момент времени одинаков.
2.2.5. Векторные формулы для скоростей и ускорений точек тела
Рассмотрим точку 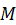 вращающегося тела, положение которой определяется радиусом-вектором
вращающегося тела, положение которой определяется радиусом-вектором  относительно полюса
относительно полюса  , взятого на оси вращения (рис. 16). Докажем, что скорость этой точки может быть выражена в виде векторного произведения по формуле Эйлера:
, взятого на оси вращения (рис. 16). Докажем, что скорость этой точки может быть выражена в виде векторного произведения по формуле Эйлера:
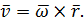
| (26) |
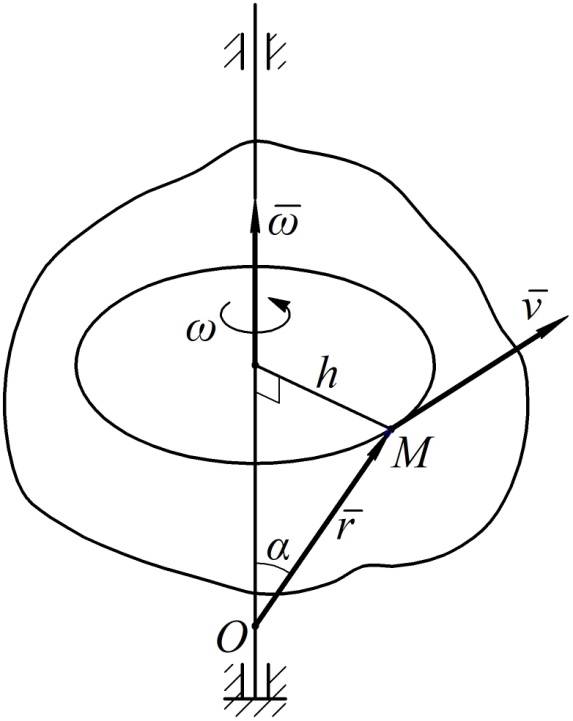 Рис. 16
Рис. 16
|
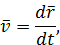
где вектор  не изменяется по величине (тело считается абсолютно твердым), но изменяет свое направление, поворачиваясь с угловой скоростью
не изменяется по величине (тело считается абсолютно твердым), но изменяет свое направление, поворачиваясь с угловой скоростью 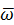 . Поэтому с использованием формулы Эйлера (26) можно вычислять производную по времени от произвольного вектора
. Поэтому с использованием формулы Эйлера (26) можно вычислять производную по времени от произвольного вектора  , не изменяющегося по величине:
, не изменяющегося по величине:
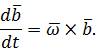
Это выражение совпадает с полученной ранее формулой (12).
Вернемся к доказательству формулы (26). Для модуля скорости имеем
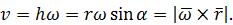
Направление вектора скорости тоже соответствует направлению векторного произведения в формуле (26).
Найдем далее вектор ускорения точки 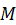 как производную от вектора скорости по времени:
как производную от вектора скорости по времени:
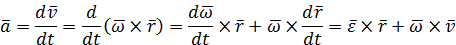
или окончательно
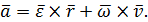
| (27) |
Для модуля вектора  имеем
имеем
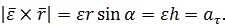
Направление векторного произведения  тоже совпадает с направлением тангенциального ускорения. Таким образом, первое слагаемое в правой части (27) есть вектор тангенциального ускорения.
тоже совпадает с направлением тангенциального ускорения. Таким образом, первое слагаемое в правой части (27) есть вектор тангенциального ускорения.
Найдем теперь модуль вектора 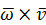 :
:

В соответствии с правилом векторного произведения направление этого вектора тоже совпадает с направлением нормального ускорения, то есть второе слагаемое в правой части (27) равно вектору нормального ускорения.
Таким образом, для ускорения точек вращающегося тела справедливы векторные формулы:
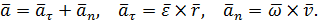
| (28) |
Пример 3
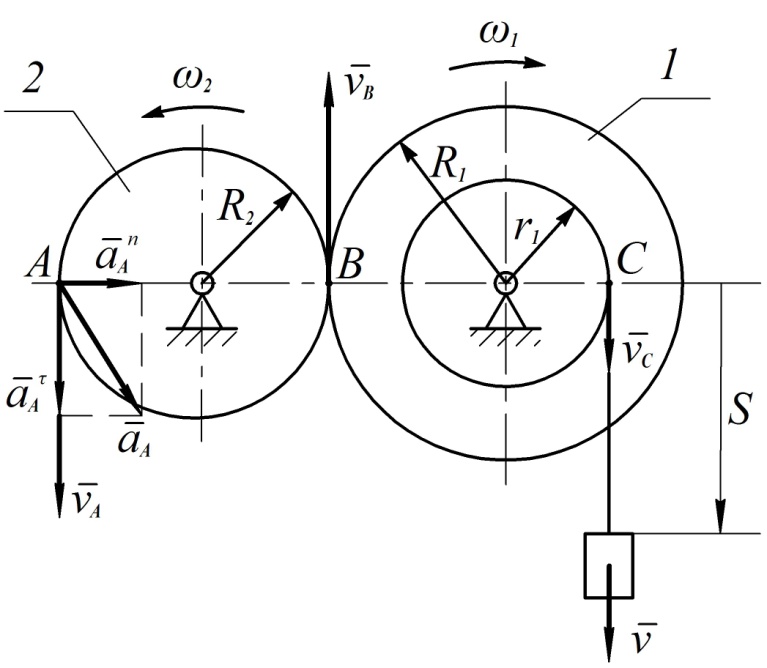 Рис. 17
Рис. 17
|
Груз опускается вертикально вниз, двигаясь по закону 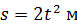 (
( 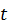 – в с). Он приводит во вращение ступенчатый шкив
– в с). Он приводит во вращение ступенчатый шкив  , посредством которого движение передается диску
, посредством которого движение передается диску 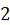 (рис. 17). Определить скорость и ускорение точки
(рис. 17). Определить скорость и ускорение точки  , лежащей на ободе диска
, лежащей на ободе диска 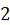 , в момент времени
, в момент времени 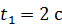 , если скольжение между дисками отсутствует. Заданы радиусы
, если скольжение между дисками отсутствует. Заданы радиусы 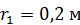 ,
, 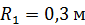 ,
, 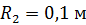 .
.
Решение
Найдем вначале скорость груза 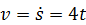 . Точка
. Точка  схода нити будет иметь такую же скорость. Теперь можно найти угловую скорость шкива
схода нити будет иметь такую же скорость. Теперь можно найти угловую скорость шкива 

Далее можно последовательно найти скорость точки зацепления дисков

угловую скорость диска 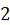
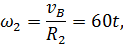
его угловое ускорение
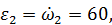
а также искомые скорость и ускорение точки  :
:
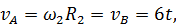


Вычислив искомые величины при 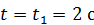 , получим окончательный ответ:
, получим окончательный ответ:
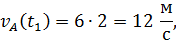
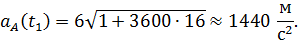
Покажем все найденные характеристики движения на рисунке.
Глава 3. Сложное движение точки
§ 3.1. Основные понятия
Пусть в пространстве движется материальная точка. Выберем две движущиеся друг относительно друга системы координат. Одну из них 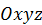 назовем основной (неподвижной), а другую
назовем основной (неподвижной), а другую 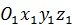 – подвижной (рис. 18). Дадим далее ряд определений.
– подвижной (рис. 18). Дадим далее ряд определений.
Движение точки, наблюдаемое из основной системы координат (то есть, видимое наблюдателем, связанным с осями 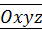 ), называется абсолютным (или сложным) движением.
), называется абсолютным (или сложным) движением.
Соответствующие характеристики движения (наблюдаемые указанным наблюдателем) будем обозначать общепринятыми буквами без индексов. Например, через 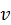 будем обозначать абсолютную скорость точки, наблюдаемую из основной системы координат, через
будем обозначать абсолютную скорость точки, наблюдаемую из основной системы координат, через 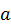 – абсолютное ускорение и т.д.
– абсолютное ускорение и т.д.
Движение точки, наблюдаемое из подвижной системы координат (видимое наблюдателем, связанным с осями 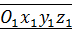 ), называется относительным движением.
), называется относительным движением.
Соответствующие характеристики движения будем обозначать с индексом 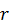 . Например, через
. Например, через 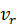 будем обозначать относительную скорость точки, наблюдаемую из подвижной системы координат и т.д.
будем обозначать относительную скорость точки, наблюдаемую из подвижной системы координат и т.д.
Движение подвижной системы координат и всех жестко связанных с ней точек, наблюдаемое из основной системы координат, называется переносным движением.
Соответствующие характеристики движения будем обозначать с индексом  . Например, через
. Например, через 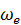 будем обозначать переносную угловую скорость (угловую скорость подвижной системы координат, наблюдаемую из основной системы координат), через
будем обозначать переносную угловую скорость (угловую скорость подвижной системы координат, наблюдаемую из основной системы координат), через  – переносную скорость точки в каком-либо ее положении (скорость точки, мысленно скрепленной с подвижной системой координат в данном ее положении, то есть, скорость точки, у которой в данном положении мысленно остановлено относительное движение) и т.д.
– переносную скорость точки в каком-либо ее положении (скорость точки, мысленно скрепленной с подвижной системой координат в данном ее положении, то есть, скорость точки, у которой в данном положении мысленно остановлено относительное движение) и т.д.
На практике обычно основную систему координат связывают с поверхностью Земли, поэтому ее часто называют неподвижной (относительно Земли).
При решении практических задач бывает полезно мысленно себе представить и построить на рисунке абсолютную, относительную и переносную траектории точки.
Приведем несколько примеров.
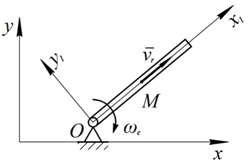
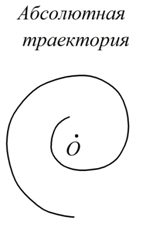 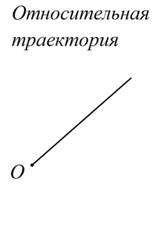 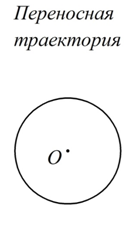 Рис. 18
Рис. 18
|
Пусть прямолинейная трубка вращается в плоскости рисунка и в трубке движется шарик 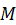 , удаляясь от оси вращения (см. рис. 18). Свяжем основную систему координат с основанием, на котором крепится ось вращения. Подвижную систему координат свяжем с трубкой. Изобразим на рисунке абсолютную, относительную и переносную траектории. Как видно из рисунка, в данном случае относительная (прямая линия) и переносная (окружность) траектории являются более простыми линиями, а абсолютная траектория (спираль) является более сложной, то есть, в результате сложения двух простых движений (по прямой и по окружности) получается более сложное движение (по спирали).
, удаляясь от оси вращения (см. рис. 18). Свяжем основную систему координат с основанием, на котором крепится ось вращения. Подвижную систему координат свяжем с трубкой. Изобразим на рисунке абсолютную, относительную и переносную траектории. Как видно из рисунка, в данном случае относительная (прямая линия) и переносная (окружность) траектории являются более простыми линиями, а абсолютная траектория (спираль) является более сложной, то есть, в результате сложения двух простых движений (по прямой и по окружности) получается более сложное движение (по спирали).
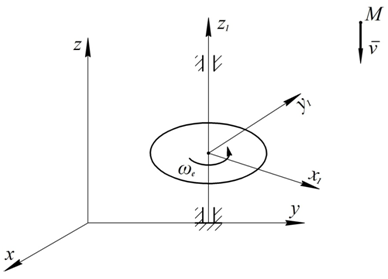
 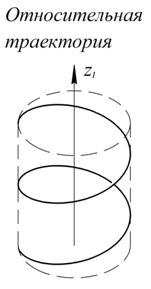 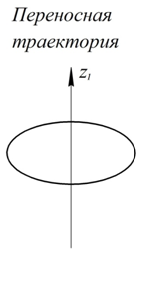 Рис. 19
Рис. 19
|
В следующем примере представим себе горизонтальный диск, вращающийся вокруг вертикальной оси (карусель), и камень 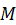 , падающий вертикально вниз на земную поверхность. Основную систему координат свяжем с поверхностью Земли. Подвижную систему координат свяжем с диском (рис. 19). Изобразим на рисунке абсолютную, относительную и переносную траектории.
, падающий вертикально вниз на земную поверхность. Основную систему координат свяжем с поверхностью Земли. Подвижную систему координат свяжем с диском (рис. 19). Изобразим на рисунке абсолютную, относительную и переносную траектории.
Здесь абсолютная траектория (вертикальная прямая) является простой линией, а относительная (нисходящая спираль на поверхности цилиндра) и переносная (окружность) траектории являются более сложными. В данном случае в результате сложения двух сложных движений (по спирали и по окружности) получается более простое (по прямой).
§ 3.2. Связь между полной и локальной производными от вектора
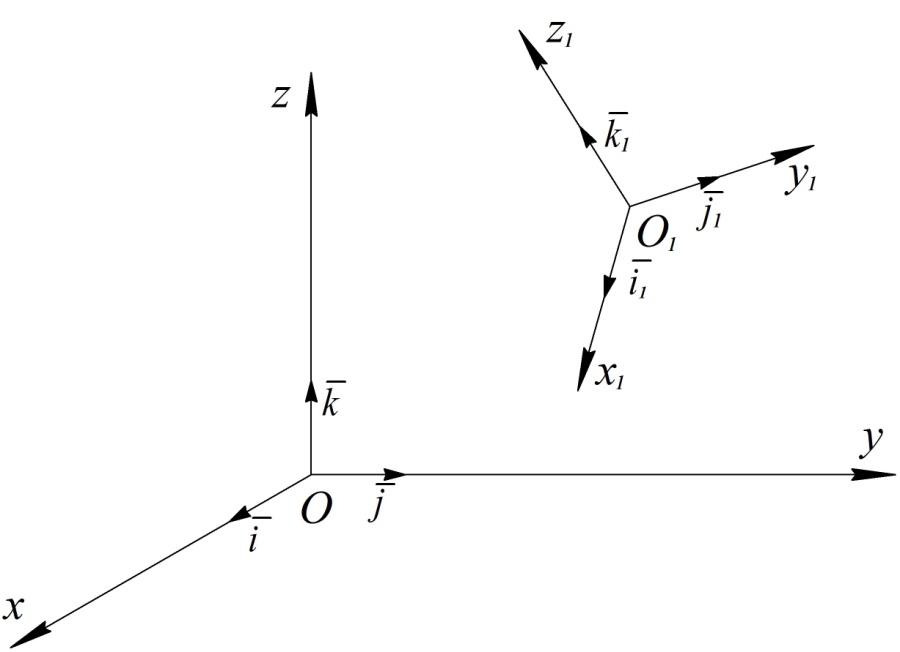 Рис. 20
Рис. 20
|
 задан в подвижной системе координат. Например, это может быть радиус-вектор точки относительно подвижной системы координат или какой-либо другой вектор. Очевидно, что изменение этого вектора со временем, наблюдаемое из основной системы координат и его изменение, наблюдаемое из подвижной системы координат, будут различными. Изменение вектора со временем характеризует его производная по времени. Производную по времени, характеризующую изменение вектора, наблюдаемое из подвижной системы координат, будем называть локальной производной и обозначать ее
задан в подвижной системе координат. Например, это может быть радиус-вектор точки относительно подвижной системы координат или какой-либо другой вектор. Очевидно, что изменение этого вектора со временем, наблюдаемое из основной системы координат и его изменение, наблюдаемое из подвижной системы координат, будут различными. Изменение вектора со временем характеризует его производная по времени. Производную по времени, характеризующую изменение вектора, наблюдаемое из подвижной системы координат, будем называть локальной производной и обозначать ее
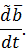
Производную по времени, характеризующую изменение вектора, наблюдаемое из основной системы координат, будем называть полной производной и обозначать ее обычным образом
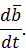
Выведем формулу, устанавливающую связь между полной и локальной производными. Обозначим проекции вектора  на оси подвижной системы координат
на оси подвижной системы координат  ,
,  ,
,  , а орты подвижной системы координат через
, а орты подвижной системы координат через 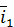 ,
, 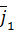 ,
, 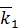 (см. рис. 20).
(см. рис. 20).
Тогда для вектора 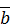 можно записать
можно записать
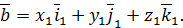
| (29) |
Вычислим локальную производную от (29), учитывая, что, с точки зрения наблюдателя, находящегося в подвижной системе координат, векторы 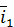 ,
, 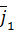 ,
, 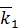 не изменяются ни по величине, ни по направлению:
не изменяются ни по величине, ни по направлению:
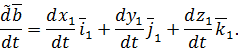
| (30) |
Найдем теперь полную производную по времени от вектора 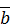 . При ее вычислении учтем, что, с точки зрения наблюдателя, находящегося в основной системе координат, орты
. При ее вычислении учтем, что, с точки зрения наблюдателя, находящегося в основной системе координат, орты 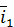 ,
, 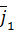 ,
, 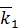 следует рассматривать как переменные векторы, которые остаются низменными по величине, но могут изменять свое направление при повороте подвижной системы координат.
следует рассматривать как переменные векторы, которые остаются низменными по величине, но могут изменять свое направление при повороте подвижной системы координат.
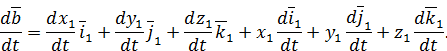
При этом производные от ортов подвижной системы координат могут быть вычислены с использованием формулы Эйлера (26):

где 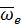 – угловая скорость подвижной системы координат. После этого для полной производной от вектора
– угловая скорость подвижной системы координат. После этого для полной производной от вектора 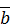 получим:
получим:
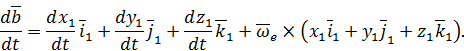
Окончательно с учетом (29) и (30) будем иметь:
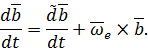
| (31) |
Эта формула, выражающая связь между локальной и полной производными по времени от вектора, впервые выведена французским ученым Буром. Поэтому ее обычно называют формулой Бура.
§ 3.3. Теорема сложения скоростей при сложном движении точки
Данная теорема устанавливает связь между скоростями точки в ее относительном, переносном и абсолютном движениях. Приведем далее ее формулировку и доказательство.
Теорема
При сложном движении точки ее абсолютная скорость равна геометрической сумме относительной и переносной скоростей.
Доказательство
Пусть движение точки рассматривается как сложное. Обозначим радиус-вектор точки 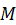 относительно основной системы координат через
относительно основной системы координат через 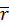 , а ее радиус-вектор относительно подвижной системы координат через
, а ее радиус-вектор относительно подвижной системы координат через 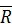 . Введем также радиус-вектор точки
. Введем также радиус-вектор точки 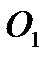 относительно основной системы координат, обозначив его
относительно основной системы координат, обозначив его 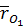 (см. рис. 21).
(см. рис. 21).
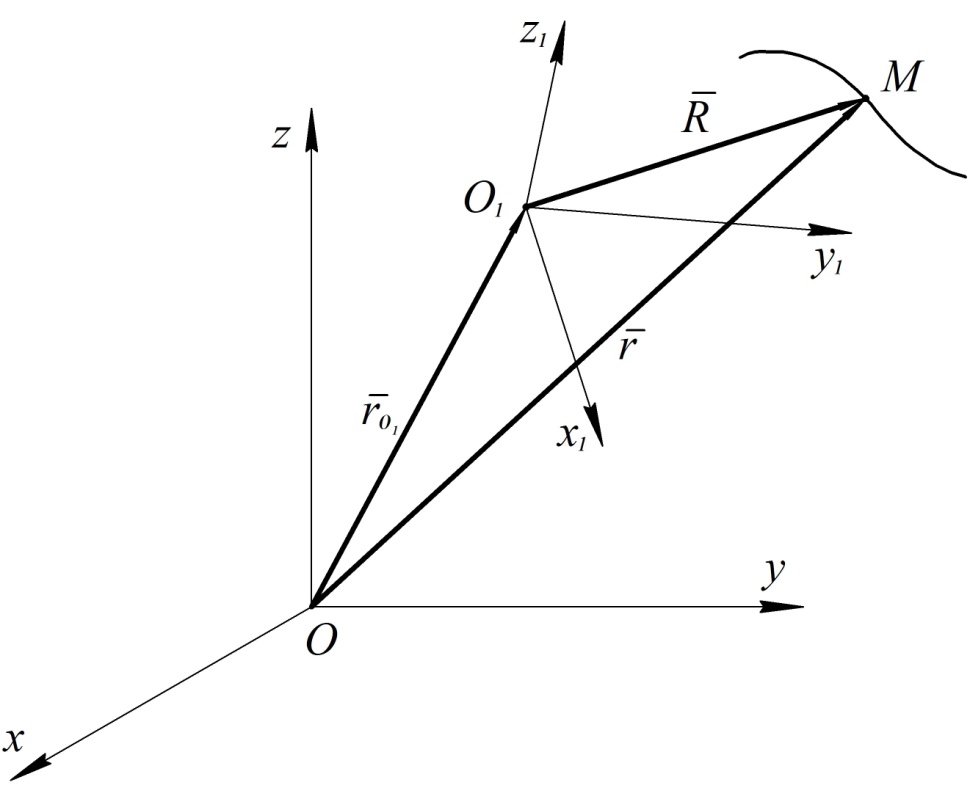 Рис. 21
Рис. 21
|
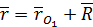
| (32) |
справедливо для любого момента времени. Продифференцируем его почленно, учитывая, что вектор 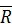 задан в подвижной системе координат и при его дифференцировании следует использовать формулу Бура (31)
задан в подвижной системе координат и при его дифференцировании следует использовать формулу Бура (31)
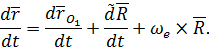
| (33) |
В выражении (33) полная производная 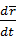 характеризует изменение радиуса-вектора
характеризует изменение радиуса-вектора 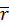 , наблюдаемое из основной системы координат. Это абсолютная скорость точки
, наблюдаемое из основной системы координат. Это абсолютная скорость точки 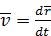 . Локальная производная
. Локальная производная 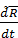 , характеризует изменение радиуса-вектора
, характеризует изменение радиуса-вектора 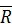 , наблюдаемое из подвижной системы координат.
, наблюдаемое из подвижной системы координат.
Это относительная скорость точки
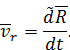
Если мысленно остановить относительное движение, положив 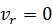 , то из формулы (33) получим выражение для переносной скорости
, то из формулы (33) получим выражение для переносной скорости
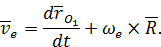
После этого векторное равенство (33) можно переписать в виде

| (34) |
что и доказывает теорему.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|