Ход решения

Ход решения

1. Заключаем прямую l 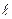в плоскость частного положения так, чтобы при пересечении конуса с плоскостью была простая линия пересечения – окружность. В данной задаче α – горизонтальная плоскость, l₂ ≡ α₂(рис.58).

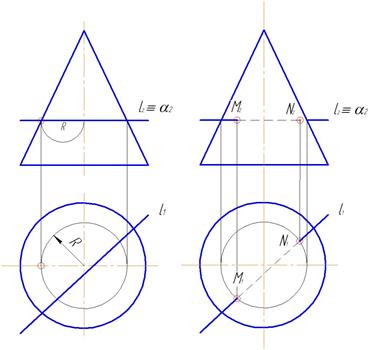
Рис. 58 Рис.59

2. Строим линию пересечения поверхности конуса с плоскостью α. Это окружность радиуса R.

3. На пересечении горизонтальной проекции l₁ и окружности радиуса R отметим искомые горизонтальные проекции M ₁ и N ₁. M ₂ и N₂ находим на фронтальной проекции l₂ прямой l.

4. Определяем видимость прямой l. Между получившимися точками M и N прямая всегда невидима на обеих проекциях, т.к. прямая находится внутри конуса. Горизонтальная проекция прямой l₁ видима (невидима только от M₁ до N₁). Фронтальная проекция l₂ до М₂ видима, т.к. точка М лежит на видимой части конуса относительно плоскости проекций П₂. Точка N лежит на невидимой части конуса относительно плоскости проекций П₂, следовательно, фронтальная проекция l₂ от N₂ до очерковой образующей невидима. За очертаниями конуса прямая l всегда видима (рис.59 ).

Пример 2.Задана призма и прямая (рис.60).

Через заданную прямую проведем вспомогательную плоскость частного положения. При пересечении гранной поверхности с плоскостью получается многоугольник, вершины которого находятся на ребрах .При пересечении этого многоугольника с заданной прямой получим искомые точки.

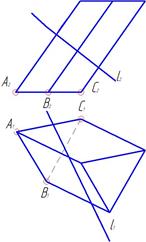
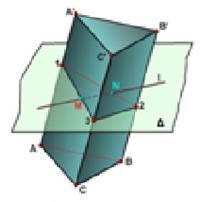
Рис.60

Ход решения:

1.Заключаем прямую l во фронтально-проецирующую плоскость α^П₂, l₂≡ α₂(рис. 61).

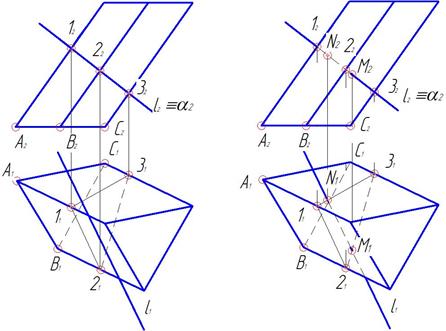
Рис.61 Рис.62

2. Строим линию пересечения плоскости α с поверхностью призмы. На фронтальной проекции отметим 1₂, 2₂, 3₂ ,в которых α₂ пересекает проекции ребер.

3. Построим горизонтальные проекции 1₁, 2₁ и 3₁ на соответствующих проекциях ребер.

4. Соединяем горизонтальные проекции1₁,2₁,3₁ломаной линией с учетом видимости. Боковая грань, примыкающая к ребру ВС основания на горизонтальной проекции невидима, т.к. это ребро невидимо. Следовательно отрезок 2-3 также не видим. Остальные ребра видимы, следовательно отрезки 1-2 и 1-3 видимы

5. На пересечении горизонтальной проекции l₁ с горизонтальной проекцией 1₁-2₁-3₁ отметим горизонтальные проекции M₁ и N₁ точек М и N.

6. Построим фронтальные проекции M₂и N₂ точек М и N на l₂.

7. Определяем видимость прямой l. Между полученными точками M и N на обеих проекциях прямая невидима всегда. Горизонтальная проекция l₁ невидима между M₁N₁ и от M₁ до горизонтальной проекции ребра В₁, т. к. горизонтальная проекция М₁принадлежит невидимой относительно π₁ грани ВС.

На П₂: точка М находится на грани BС видимой относительно П₂, следовательно, М₂видима и фронтальная проекция l₂видима до М₂. Точка N принадлежит грани А C, невидимой относительно П₂, следовательно, фронтальная проекция N₂ не видима и фронтальная проекция l₂от N₂невидима. За очертаниями призмы прямая l видима (рис. 62).

Задача 9.Построить три проекции геометрического тела с вырезом. Выполнить задачу 9 на формате А3.

Данная задача показана на 5 примерах разных геометрических тел.

Пример 1. Вырез на конусе (рис. 63).

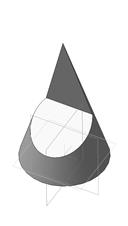
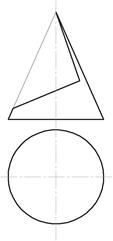
Рис. 63

Вырез произведен двумя фронтально-проецирующими плоскостями. Плоскость α проходит через вершину конуса и рассечет его поверхность по образующим – двум прямым.. Вторая плоскость β – фронтально-проецирующая, линия пересечения – часть эллипса, ограниченная прямой принадлежащей линии пересечения плоскостей CN(рис.64).

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒