Ход решения

Ход решения

1. Через прямую l проводим вспомогательную плоскость частного положения, например, горизонтально-проецирующую α П_1, l₁ ≡α₁ (рис. 45).

2. Строим линию пересечения MN заданной и вспомогательной плоскостей. М₁=А₁С₁∩ α_1, М₂ А₂С₂ и N₁=В₁С₁∩α _1,N₂ В₂С₂ (рис. 46).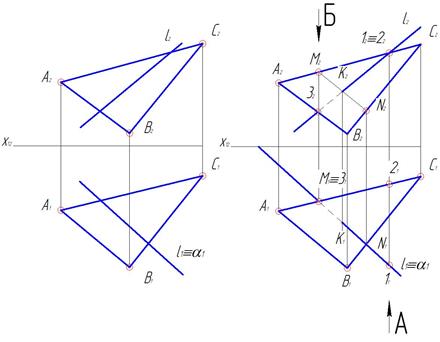

Рис. 45 Рис.46

3. Строим точку пересечения К заданной прямой l с линией пересечения МN. К₂= М₂N₂∩l₂. К₁находится на М ₁N₁.

4. Определяем видимость прямой относительно ΔАВС с помощью конкурирующих точек.

Определяем видимость на плоскости П₂.Отметим фронтальную проекцию 1₂, совпадающую с 2_2. Горизонтальную проекцию 2₁отметим на А₁С₁, а 1₁ на l₁. Горизонтальная проекция 1₁ лежит перед 2₁, следовательно, точка 1 видима на П₂. Точка 1 лежит на прямой l, она видима на П₂, следовательно фронтальная проекция l₂ до К₂видима, в точке К₂ видимость меняется на невидимую .

Определим видимость прямой l на П₁. Отметим горизонтальную проекцию 3₁совпадающую с горизонтальной проекцией М₁. М₂ 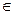А₂С₂ уже отмечена, 3₂ 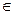l₂. Фронтальная проекция М₂лежит выше фронтальной проекции 3₂, следовательно, точка М видима на П₁ .Плоскость закрывает прямую l до К₁, горизонтальная проекция l₁ невидима. В горизонтальной проекции К₁ видимость меняется на видимую . За границами ΔАВС прямая l видима.

Задача 6.Построить линию пересечения плоскости общего положения с заданной поверхностью.

Пример 1. Трехгранная призма (рис.47).

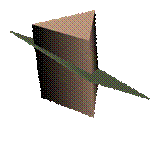
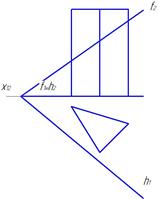
Рис.47

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒