Техника расчета

1. Точно против условного среднего класса проставляют черточки (в первом ряду - одну, во втором - три).

2. Простым суммированием ведется накопление частот от краев к центру до встречи с центральными черточками (по ходу стрелок, проставленных для наглядности). Сначала накапливаются частоты в первом ряду, затем во втором.

3. Определяются суммы накопленных частот р₁, q₁, p₂, q₂:

p₁ - сумма накопленных частот верхней части первого ряда суммирования, равная 53.

q₁ - сумма накопленных частот нижней части первого ряда суммирования, равная 126.

p₂ и q₂ - то же для второго ряда суммирования, соответственно равные 43 и 126.

4. При расчете данным способом может быть проведена проверка правильности расчета.

Сумма трех чисел - частоты условного среднего класса (22) и чисел, ближних к черточке в первом ряду (27 и 51), должны быть равны числу выборки (n =100). В данном случае: 22+27+51=100.

Сумма двух чисел, ближних к черточкам первого и второго рядов верхней части ряда суммирования, равна числу р₁:

22 + 26 = 53

Сумма двух чисел, ближних к черточкам первого и второго рядов нижней части ряда суммирования, равна числу q₁:

51 + 75 = 126

5. По полученным величинам р₁, р₂, q₁ и q₂ вычисляют две суммы S₁ и S₂ с учетом знаков. Эти величины только по способу расчета отличаются от основных величин, получаемых при расчете способом произведений. По своей конечной величине S₁ = åfa;

S₂ = åfa²

S₁ = q₁ – p₁ = 126 – 53 = 73; S₁ = 73

S₂ = p₁ + q₁ +2(p₂ + q₂) =53+126+2 (43+126) =179+2´169 = 179+338 = 517; S₂ = 517 .

6. По основным формулам рассчитываются необходимые параметры:

= A + K 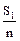; = 105 + 10 = 105 + 7,3 = 112,3

C = 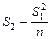= = 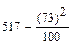517 - 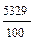= 463,71

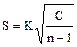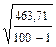=10 = 10 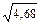= 21,6 .

ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ И ВЫБОРКА. РЕПРЕЗЕНТАТИВНОСТЬ ВЫБОРОЧНЫХ ПОКАЗАТЕЛЕЙ

Весь массив объектов определенной категории, представляющий интерес для исследования, называется генеральной совокупностью. Теоретически - это бесконечно большая или, во всяком случае, приближающаяся к бесконечности совокупность единиц или членов, которые могут быть к ней отнесены. Сущность этого понятия хорошо выражается в испанском языке, на котором "генеральная совокупность" называется словом "universo", что в то же время означает "вселенная".

Обычно генеральная совокупность включает очень большое число объектов: все животные данного биологического вида, поголовье птицы одной породы или одной линии, количество эритроцитов в крови одного животного. Многочисленность составляющих генеральную совокупность единиц в большинстве случаев очень сильно затрудняет или вообще делает невозможным полное ее изучение. В ряде случаев, если поставить задачу полного изучения генеральной совокупности, то потребуется разрушить, уничтожить ее. Так, например, если нужно определить массу яичников у всех кур определенного хозяйства, кур нужно забить, т. е. ликвидировать хозяйство; если требуется изучить состав всей крови животного, придется выпустить всю кровь из организма, т. е. убить животное. Иногда изучаемая совокупность бывает небольшая, в частности, в том случае, если исследователя интересует продуктивность птицы только в одном птичнике, тогда необходимо изучить только 2000-2500 голов птицы.

Сплошное изучение генеральных совокупностей производится редко (перепись населения). Практически же в подавляющем большинстве случаев исследованию подвергается всего лишь часть генеральной совокупности, называемая выборкой. Как правило, выборка - это достаточно небольшая часть генеральной совокупности, но она изучается с целью характеристики всей совокупности. Для достаточно точной характеристики генеральной совокупности параметры выборки должны достаточно правильно соответствовать параметрам генеральной совокупности, т. е. быть репрезентативными (representar - представлять).

Для того, чтобы выборка могла характеризовать генеральную совокупность, следует правильно организовать случайный отбор объектов в эту выборку. При этом совершенно недопустима тенденциозность, предвзятость при выборе объектов, нельзя отбирать только лучшие или только средние объекты, или часть лучших, часть средних и часть худших и т.д. В процессе опыта недопустимо исключать из подопытных групп отдельных особей, почему-либо не устраивающих экспериментатора.

Для получения неискаженной характеристики всей генеральной совокупности необходимо стремиться к тому, чтобы в выборку мог попасть любой объект из любой части генеральной совокупности. В этой связи при выборе объектов для опыта применяется принцип случайности (англ. - sample random test, исп. - al azar).

В зависимости от характера исследования может применяться один из следующих способов отбора объектов в выборку (рассматриваются наиболее употребимые способы):

1. Случайный бесповторный отбор. Объекты для исследования отбираются из генеральной совокупности случайно и обратно в нее не возвращаются. Повторно в выборку попасть не могут. Наиболее распространенный способ отбора из большой, но ограниченной генеральной совокупности. Пример - отбор кур в хозяйстве для вскрытия с целью исследования на гельминты.

2. Случайный повторный отбор. Объекты отбираются в выборку в случайном порядке и после изучения обратно возвращаются в генеральную совокупность. Метод равносилен отбору из бесконечно большой генеральной совокупности. Пример применения - при исследовании развития молодняка птицы случайно отобранной из птичника небольшая партия цыплят взвешивается, после чего цыплята возвращаются в птичник. При повторном взвешивании возможно вторичное попадание отдельных цыплят в случайную выборку.

3. Механический отбор. Отбор объектов из генеральной совокупности производится из отдельных ее частей, которые предварительно намечаются механически по определенной системе. Пример - отбор яиц для анализа по принятой системе из ячеек (по 3, 4 или 6 из каждой ячейки или из части ячеек) в определенном геометрическом порядке. В зависимости от объекта намечается, из скольких частей (ячеек) совокупности отбираются объекты и по сколько образцов (яиц) из каждой части.

4. Серийный гнездовой отбор. В этом случае генеральная совокупность разбивается на части - серии или гнезда. Некоторые серии исследуются целиком и по результатам исследования делается характеристика всей генеральной совокупности. В частности, для получения данных по продуктивности животных в районе можно провести изучение необходимых показателей у всего поголовья в нескольких отдельных хозяйствах. Идеальное осуществление отбора - проведение его методом жеребьевки или же посредством таблицы случайных чисел, позволяющей исключать субъективизм при отборе.

При всяком исследовании есть вероятность допустить ошибки, искажающие истинную картину. Эти ошибки могут быть самого разного характера, однако все их можно подразделить на две основные категории:

А. Категория ошибок, которые можно избежать или свести к минимуму при тщательной организации исследований. К ним относятся:

1) ошибки методического характера, вызванные неправильно избранной методикой исследований;

2) ошибки точности, вызванные употреблением непроверенных измерительных приборов;

3) случайные ошибки, происходящие в результате описок, перепутывания образцов и т. д.;

4) ошибки типичности, обусловленные неправильным, без учета всех условий, отбором объектов в выборку.

Б. Поскольку часть никогда не может полно характеризовать целое, при выборочном исследовании существует особый тип ошибок, вытекающих из самой сущности такого исследования. Таких ошибок избежать невозможно. Они называются ошибками репрезентативности, так как показывают, насколько выборочные параметры отличаются от соответствующих показателей генеральной совокупности, насколько точно они ее представляют, т. е. насколько они репрезентативны. Этих ошибок нельзя избежать, но их можно учесть, и следует стремиться к уменьшению их величины. Существуют способы расчета ошибок этой категории.

Ошибка репрезентативности арифметической средней зависит от двух величин: степени разнообразия признака и численности выборки. Ошибка тем больше, чем выше разнообразие признака. Чем больше численность выборки, тем большая часть генеральной совокупности исследуется и меньше ошибка репрезентативности арифметической средней (рис. 3).

На основе этой закономерности наиболее применимы следующие формулы расчета ошибки репрезентативности средней арифметической:

= ; =

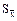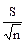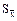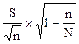
(первая формула применяется при бесконечной генеральной совокупности, вторая - в том случае, если объем генеральной совокупности известен).

Поскольку ошибка прямо пропорциональна изменчивости признака, в числителе формулы стоит среднее квадратическое отклонение (S). Обратная зависимость ошибки от численности выборки отражена тем, что в знаменателе формулы стоит "n".

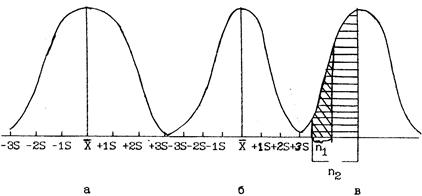
Рис. 3. Зависимость ошибки репрезентативности от разнообразия признака и объекта выборки:

а - распределение признака с высокой вариабельностью; б -распределение признака с низкой вариабельностью; в - небольшая выборка (n₁) и большая выборка (n₂)

Пример расчета. В качестве примера расчета ошибки средней арифметической можно использовать материалы по массе яиц от группы кур: = 57,14; S = 4,58; n = 60.

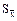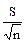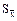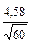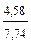= ; = = = 0,59; 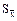= 0,59

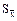± = 57,14 ± 0,59 .

ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ. ТРИ СТЕПЕНИ ВЕРОЯТНОСТИ ПРИ ОПРЕДЕЛЕНИИ ГЕНЕРАЛЬНЫХ ВЕЛИЧИН. КРИТЕРИЙ СТЬЮДЕНТА

В предыдущих разделах отмечалось, что во всяком нормальном распределении в установленных границах значений признака имеется определенная доля дат. Доля дат, ограниченная тем или иным числом средних квадратических отклонений, может быть определена по второй функции нормированного отклонения. Не вдаваясь в подробности рассмотрения этого вопроса, можно отметить, что вторая функция нормированного отклонения определяется по формуле:

j₍_c) = ,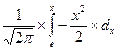

где j₍_c₎ - обозначение второй функции нормированного отклонения; c- нормированное отклонение заданной величины признака;p = 3,14; е - основание натурального логарифма, равное 2,718. (Нормированное отклонение показывает, на сколько сигм отклоняется значение признака от средней для соответствующей группы.)

Величина j₍_c₎, или вторая функция нормированного отклонения указывает ту долю дат, которые находятся между средней арифметической и заданной величиной признака. Значение j₍_c₎ или долю дат можно найти по таблице интеграла вероятностей, так что расчет по указанной формуле не всегда обязателен.

В частности, определяем, какая доля дат ограничивается значением одной сигмы (учитывая, что сигма является мерой изменчивости в пределах данного вариационного ряда). Из таблицы интеграла вероятностей следует, что в границах от до + S имеется 0,341, или 34,1% всех дат данного вариационного ряда. Такое же количество дат находится и в границах - S.

Следовательно, в границах ± S имеется 0,683, или 68,3% всех дат вариационного ряда. Это значит, что 68,3% всех дат по своему значению не отличаются от средней величины более чем на ±1S. Если примем за границы ±2S, найдем, что процент дат, отличающихся от средней не более чем на ±2S, равен 2j = 2 0,477 = 0,954, или 95,4%, т. е. в границах от - 2S до + 2S укладывается 95, 4% дат, а за эти пределы выходит только 4-6% дат. При ± 3S внутри границ окажется 2j-=2 0,4986 = 0,997, или 99, 7% дат, вне этих границ только 0,3% дат.

В границах ± 4S имеется 2j = 2 0,49997 = 0,99994, или 99,94% всех дат, и только 0,06% вне их.

В дальнейшем применяется показатель "t", указывающий, на сколько средних квадратических отклонений данная величина отличается от средней. Этот показатель называется нормированным отклонением и рассчитывается по формуле: t = .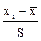

Доли особей, находящиеся в пределах ± tS (t = 1,2,3,4), указывают на ту вероятность, с которой взятая наугад особь будет иметь значение признака, отличающееся от средней не более чем на tS, или любая средняя будет больше или меньше генеральной средней не более чем на t .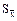

Это предположение допускается во всех случаях при определении выборочных показателей и имеет характер основной гипотезы всякого биометрического исследования. Определение любого биометрического показателя невозможно без предварительного установления условных границ вероятности того, что взятая наугад дата окажется в заданных пределах. Эта гипотеза применяется при определении достоверности разности двух выборочных величин, достоверности коэффициента корреляции и т.д.

Данные таблицы 16 показывают, что 68,3% вероятности того, что в интервале ± 1S может быть заключена генеральная средняя, является сравнительно невысоким уровнем: вероятность ошибки здесь составляет 1 случай из 3. С большей уверенностью можно утверждать, что генеральная средняя покрывается интервалом 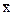± 2S, так как вероятность здесь равна 95,4%, возможность ошибки - 1 случай из 22.

При интервале в 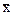± 3S практически можно быть уверенным в правильности суждения, поскольку возможность ошибки здесь достаточно мала - 1 случай из 370 возможных. Фактически все распределение полностью укладывается в пределах 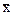± 4S, вероятность правильного суждения здесь 99,9936%, возможность ошибки составляет всего 1 случай на 15625 возможных.

Таблица 16

Вероятность (Р) нахождения любой даты в пределах 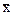± tS

t	Вероятность нахождения				Возможность ошибочного суждения
t	в пределах ± tS		вне пределов ±tS		Возможность ошибочного суждения
4,0		0,999935		0,000064		1 : 15625
3,3		0,99900		0,001000		1 : 1000
3,0		0,99730		0,00270		1 : 370
2,58		0,99000		0,01000		1 : 100
2,5		0,98758		0,01242		1 : 81
2,0		0,95450		0,04550		1 : 22
1,96		0,95000		0,05000		1 : 20
1,0		0,68268		0,31732		1 : 3

Как видно, вероятность отклонения от средней величины более чем на 3S очень мала. Эта закономерность обосновывает правило трех сигм. Три величины стандартного отклонения (три сигмы) как бы ограничивают пределы случайного рассеяния внутри вариационного ряда. То, что находится в пределах ±3S, относится к данному вариационному ряду, то, что за этими пределами, вероятнее всего к нему не относится.

Чем выше требования к вероятности вывода, тем шире должен быть интервал, который может обеспечить ее достоверность. Уровень этой вероятности принято называть доверительной вероятностью, или надежностью.

В настоящее время применяются три степени вероятности того, что заключение о границах, вмещающих все распределения, будет достоверным. Для удобства работы применяют "круглые" числа:

1 уровень - 95%

2 уровень - 99%

3 уровень - 99,9% .

В этих случаях границы доверительного интервала составляют соответственно:

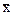± 1,96S

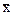± 2,58S

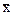± 3,30S .

Обычно значения показателей вероятности обозначаются через Р (Probability), соответственно чему делаются записи при указании уровней вероятности или уровней значимости:

P ³ 0,95 или P ≤ 0,05

P ³ 0,99 или P ≤ 0,01

P ³ 0,999 или P ≤ 0,001 .

Определенному значению вероятности соответствует уровень значимости. Так, вероятности 0,95 (95%) соответствует уровень значимости 0,05 (5%), вероятности 0,99 (99%) - уровень значимости 0,01 (1%). Уровень значимости показывает, с какой вероятностью возможна ошибка в результатах опыта. В научных публикациях при оценке достоверности результата может указываться или уровень вероятности, или уровень значимости.

Какой уровень вероятности может считаться достаточным при оценке результатов исследования? В каких случаях можно довольствоваться одним уровнем и когда требуется более высокий уровень вероятности суждения?

Первый уровень вероятности, соответствующий 95% доверительному интервалу (Р³0,95), считается достаточно надежным для оценки результатов большинства биологических исследований (общая биология, цитология, физиология, генетика, ботаника, зоология, зоотехния, ветеринария, медицина). В этом случае t уровень равен 1,96, выборочная средняя от генеральной отличается не более чем на 2 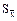. Вероятность ошибки 1:20 считается допустимой. Большую вероятность ошибки, как, например, 1:10 при Р ³ 0,90, в этих исследованиях допускать не следует.

Второй уровень вероятности в 99% (Р³0,99) требуется в экономических исследованиях, связанных с затратами труда и денежных средств. В этом случае допускается возможность ошибки 1:100, t=2,58, выборочная средняя отличается от генеральной не более чем на 2,58× 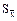. Этот уровень вероятности применяется также при повторных биологических исследованиях, если предшествующие эксперименты вызывают сомнения и требуют уточнения.

Третий уровень вероятности Р³0,999, соответствующий 99,9% уровню вероятности безошибочного суждения, отвечает самым высоким требованиям надежности результатов эксперимента. В этом случае возможность ошибки составляет всего лишь 1:1000. Такая высокая степень вероятности требуется при особо ответственных работах, а именно: в экспериментах с вредными и ядовитыми веществами, при проверке спорных теоретических вопросов и др.

Указанные выше взаимосвязи показателей t и соответствующих степеней вероятности справедливы в исследованиях на достаточно многочисленных выборках. Если же в исследованиях взята небольшая, малочисленная выборка, то распределение выборочных величин достаточно сильно отличается от нормального, а значит, не подчиняется закономерностям нормального распределения. В таких случаях оно следует закону распределения малых выборок, установленному английским ученым В.Госсетом (1876-1937), подписывавшим свои работы псевдонимом Student (Стьюдент). Распределение Стьюдента отличается от нормального тем больше, чем меньше объем изучаемой выборки.

Значения величины t для трех степеней вероятности и для любого объема выборки приводятся в таблице 17 значений критерия Стьюдента.

Таблица 17

Таблица значений критерия t (критерия Стьюдента)

Число степеней свободы	Значение t			Число степеней свободы	Значение t
Число степеней свободы	Р=0,95	Р=0,99	Р=0,999	Число степеней свободы	Р=0,95	Р=0,99	Р=0,999
	12,7	63,7	637,0		2,2	3,0	4,1
	4,3	9,9	31,6	14-15	2,1	3,0	4,1
	3,2	5,8	12,9	16-17	2,1	2,9	4,0
	2,8	4,6	8,6	18-20	2,1	2,9	3,9
	2,6	4,0	6,9	21-24	2,1	2,8	3,8
	2,4	3,7	6,0	25-28	2,1	2,8	3,7
	2,4	3,5	5,3	29-31	2,0	2,8	3,7
	2,3	3,4	5,0	32-34	2,0	2,7	3,7
	2,3	3,3	4,8	35-42	2,0	2,7	3,6
	2,2	3,2	4,5	43-62	2,0	2,6	3,5
	2,2	3,1	4,4	63-175	2,0	2,6	3,4
	2,2	3,1	4,3	175 и более	2,0	2,6	3,3

Таким образом, для каждого значения численности выборки определяется своя величина t для трех степеней вероятности. Например, для степени вероятности Р = 0,95 при численности выборки n = 30 (и больше) показатель t = 2,0. При n = 10 t = 2,3; при n = 3 показатель вероятности t = 4,3, а при n = 2 t = 12,7.

При использовании этой таблицы для нахождения соответствующего значения критерия t необходимо брать ту строку, которая соответствует числу степеней свободы, т. е. числу n - 1, если n -численность выборки.

ДОВЕРИТЕЛЬНЫЕ ГРАНИЦЫ ГЕНЕРАЛЬНОЙ СРЕДНЕЙ. ДОСТОВЕРНОСТЬ РАЗНОСТИ ДВУХ ВЫБОРОЧНЫХ СРЕДНИХ ВЕЛИЧИН И ДВУХ ДОЛЕЙ

Доверительные границы генеральной средней

Для того чтобы определить, чему равняется генеральная средняя величина, рассчитываются два возможных ее значения - минимальное и максимальное. Крайние значения, в пределах которых может находиться генеральная средняя, называются генеральными границами. При расчете этих границ исходят из того, что генеральная величина может отстоять от выборочной величины (например, генеральная средняя арифметическая от выборочной средней арифметической) не более чем на величину t-кратной ошибки репрезентативности выборочного показателя. При этом величина t устанавливается в зависимости от следующих условий:

а) ответственности исследования - I, II, III уровни вероятности;

б) объема выборки: при малом числе показателей, отобранных в выборку, t устанавливается по таблице Стьюдента.

Применяется формула 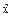= 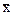± t .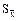

Это значит, что величина генеральной средней может иметь следующие значения: не менее 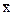– t 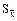и не более 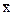+ t .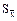

Пример. В птичнике методом механического отбора отобрано 60 яиц и произведено их взвешивание. Получены следующие данные, характеризующие эту выборку:

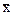= 57,14 г; S = 4,58; 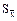= 0,59.

На основе этих данных можно сделать заключение, какова средняя масса яйца в этом птичнике в данный период, т. е. чему равна генеральная средняя по массе яйца в этом птичнике:

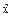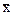= ± tS_х

для Р ³ 0,95 и n = 60 показатель t = 2.0.

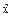= 57,14 ± 2 ´0,59 = 57,14 ± 1,18

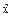= 55,96 : 58,32 56 ¸ 58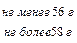

Это значит, что средняя величина яйца по всему птичнику лежит в пределах от 56 до 58 г.

Пример. При нарушении кальциевого питания кур-несушек в их организме произошли изменения минерального обмена, а вследствие этого изменения в костяке. Изменения, произошедшие в скелете, определялись (в целях диагностики) измерением толщины стенки бедренной кости. Обследовано 23 больные курицы и (для контроля) 8 здоровых. Получены следующие данные:

для больной птицы 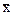₁ = 0,68 мм; 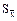= 0,055 мм

для здоровой птицы 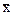₂ = 1,71 мм; 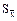= 0,159 мм .

При Р³0,95 находим по таблице Стьюдента t₁ = 2,1 и t₂ = 2,3.

Рассчитываем генеральные параметры:

для больной птицы: 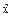₁ = 0,68 ± 2,1´0,055 = 0,68 ± 0,115

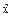₁ =0,565 ¸ 0,795; 0,56 ¸ 0,80

для здоровой птицы: 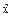₂ = 1,71 ± 2,3´0,159 = 1,71 ± 0,366

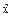₂ = 1,344 ¸ 2,076; 1,34 ¸ 2,1 .

Несмотря на очень широкие пределы генеральной средней, что обусловлено малым объемом выборки (особенно для здоровой птицы), измерение толщины стенки бедренной кости оказалось достоверным объективным показателем, отражающим состояние минерального обмена в организме птицы. На основании полученных данных можно сказать, что у здоровой птицы средняя толщина стенки бедренной кости должна быть не менее 1,34 мм, у больной она не превышает 0,80 мм.

Достоверность разности двух средних величин

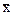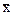В научных исследованиях очень часто необходимо сравнивать две (или больше) арифметические средние величины. Это сравнение достигается определением разности двух величин: D = ₁ - ₂.

При статистическом анализе важно получить ответ на вопрос: насколько разность выборочных средних правильно отражает различие соответствующих генеральных средних, или насколько достоверна выборочная разность?

Достоверность выборочной разности измеряется особым показателем достоверности разности - t_d. Критерий достоверности разности средних рассчитывается по формуле:

t_d = ,

где 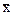₁ - 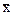₂ - разность средних величин; 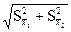- ошибка разности средних. Критерий t_d не имеет знака, следовательно, знак разности средних во внимание не принимается.

Каждая выборочная средняя имеет свою ошибку репрезентативности, поэтому разность между ними тоже имеет свою ошибку репрезентативности.

Определение достоверности выборочной разности с практической точки зрения сводится к вопросу обобщения результатов, полученных в эксперименте, т. е. насколько возможно полученные в выборке данные перенести на генеральные совокупности.

Как видно из формулы, достоверность выборочной разности определяется ее отношением к собственной ошибке. Разность считается достоверной (значимой), если критерий достоверности разности (t_d) равен или превышает принятый в исследовании показатель вероятности безошибочного суждения (по таблице значений критерия Стьюдента):

t_d ³ t_d_0,95 - I уровень вероятности

или t_d ³ t_d_0,99 - II уровень вероятности

или t_d ³ t_d_0,999 - III уровень вероятности.

Полученные в этих расчетах результаты можно разделить на две категории.

1. При t_d ³ t_d _st разность достоверна (значима). Это значит, что выводы, полученные в выборочной разности, можно перенести на генеральную разность. Иными словами, если средняя величина первой выборочной больше средней величины второй выборочной, то средняя всей первой генеральной совокупности больше средней второй генеральной совокупности.

2. При t_d < t_d _st разность недостоверна. Это значит, что выводы, полученные при сравнении выборочных средних, нельзя перенести на соответствующие генеральные совокупности. При этом важно понять, что отсутствие достоверности выборочных величин не позволяет сделать никаких определенных выводов - ни о наличии, ни об отсутствии различий между соответствующими генеральными средними величинами.

Разность может быть недостоверной либо вследствие недостаточного объема изучаемой выборки, либо из-за отсутствия разницы между изучаемыми генеральными совокупностями.

Пример. В эксперименте изучалось действие добавок в кормосмеси птицы кальция и витамина С на толщину скорлупы яиц. Группа I получила в рационе 3,1% кальция, группа II – 4,1% кальция и 50 мг витамина С на 1 кг кормосмеси. Для исследования брались выборки по 40 яиц в каждой группе. Скорлупа измерялась в трех точках яйца - по экватору, в тупом и остром конце, за основу принимались средние величины. Получены следующие данные:

в I группе: 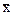₁= 0,3216 мм; 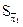= 0,00364; n₁ = 40

во II группе: 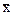₂= 0,3461 мм; 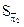= 0,00317; n₂ = 40

t_d_1-2 = ; t_d_1-2 = =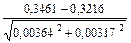

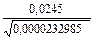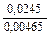= = 5,05; t_d_1-2 = 5,05

Число степеней свободы n = n₁ + n₂ – 2 .

Следует обратить внимание на то, что в данном случае при определении числа степеней свободы вычитается величина 2. Это определяется тем, что число степеней свободы рассчитывается для двух средних арифметических, следовательно, имеется два (элемента) ограничения свободного разнообразия. Продолжая расчет, находим:

n = 40 + 40 – 2 = 78. Согласно таблице критерия Стьюдента при n = 78:

t_0,95 = 2,0

t_0,99 = 2,6

t_0,999 = 3,4 или t_st = 2,0 - 2,6 - 3,4 .

Полученное в расчете значение t_d больше, чем t_0,999по таблице Стьюдента, т. е. t_d > t_0,999, так как 5,05 > 3,4. Это говорит о том, что в эксперименте имеется достоверное увеличение толщины скорлупы при III уровне достоверности (Р³0,999). Значит, в аналогичных условиях содержания птицы указанный уровень кальция и витамина С всегда обеспечит увеличение толщины скорлупы яйца.

При отсутствии таблицы можно исходить из правила трех сигм: если разница средних превышает ошибку разности почти в три раза, она достоверна с вероятностью не менее 0, 99.

Выборочные доли и достоверность их разности

В зоотехнических исследованиях нередко приходится иметь дело с таким материалом, когда весь объем изучаемой выборки распределяется на две части по наличию или отсутствию у изучаемых объектов того или иного признака. Такие признаки называются качественными, или альтернативными. В частности, при инкубировании партии яиц из одной части выводятся цыплята, из другой нет. Таким образом, заложенная в инкубатор партия яиц разделяется на две доли, которые могут быть выражены в процентах. Для выборочной доли можно рассчитать ошибку репрезентативности. Основываясь на свойствах выборочной доли, можно рассчитать достоверность разности двух выборочных долей, в частности, достоверность процента выводимости из двух сравниваемых партий яиц.

При расчете принимаются следующие обозначения:

р - доля объектов, обладающих признаком;

q = 1 - р - доля объектов, не обладающих изучаемым признаком.

Квадратическое отклонение доли S = 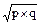. Особенность квадра-тического отклонения доли заключается в том, что оно никогда не бывает больше 0,5, т.е. S_max = 0,5. Ошибка репрезентативности доли находится из основной формулы ошибки:

S_p = = = 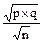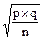; S_p = .

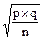При определении достоверности разности двух долей применяется формула критерия достоверности разности:

t_d = ,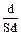

где d = p₁ – p₂ - разность долей;

S_d = 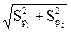= - ошибка разности долей.

Критерий достоверности разности двух долей составляет:

t_d =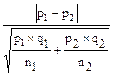

Уровень достоверности разности долей определяется сопоставлением полученного значения t_d со значениями критерия по таблице Стьюдента, соответствующими трем степеням вероятности безошибочного суждения (Р₁= 0,95; Р₂= 0,99; P₃ = 0,999).

Число степеней свободы определяется как n₁ + n₂ - 2, где n₁ и n₂ - число всех определений в каждой выборке.

Пример. С целью определения влияния продолжительности хранения инкубационных яиц в условиях тропического лета на выводимость цыплят проведено сравнительное инкубирование двух партий яиц. Яйца первой партии до закладки в инкубатор хранились при температуре +30.. +32°С в течение четырех суток. Яйца второй партии находились в аналогичных условиях только одни сутки.

От первой партии заложено в инкубатор 134 яйца, вывелось 106 цыплят I категории, процент выводимости – 80,6%. От второй партии заложено в инкубатор 162 яйца, вывелось 148 цыплят I категории, процент выводимости составил 91,4%.

Какова достоверность разности между выводимостью первой и второй партий яиц?

Доли составляют p₁ = 0,806 и q₁ =0,194 для первой и p₂ = 0,914 и q₂ = 0,086 для второй партии.

Для обеих партий яиц находим квадраты ошибок репрезентативности:

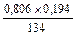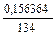= = = 0,0011; 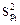= 0,0011

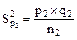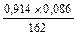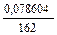= = = 0,00048; 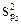= 0,00048 .

Разность двух долей составляет р₁ – p₂= 0,914 – 0,806 = 0,108. Подставляем полученные значения в формулу t_d - критерия:

t_d = 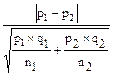= = 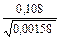2,72.

Число степеней свободы в настоящем расчете составило:

n = 134 + 162 – 2 = 294 .

Согласно таблице значений критерия Стьюдента при таком числе степеней свободы фиксированные значения критерия следующие:

t_st = 2,0 – 2,6 – 3,3.

Полученный показатель t_d, равный 2,72, больше фиксированного значения t_st, соответствующего второму уровню вероятности. Значит, разность между выводимостью двух изуч

⇐ Предыдущая 8 9 10 11 12 13 14 15 1617