Питання для самоперевірки

План

3. Вектор: означення, координати, напрямні косинуси, базис.

4. Лінійна залежність і незалежність векторів.

5. Розклад вектора за базисом.

$Література:

К. Т. Валєєв, І. А. Джалладова. Вища математика, ч.1, К,2001р.

М.К. Бугір Математика для економістів. - К.: Академія, 1998.р.1. §4.стр.13-16

О.І. Соколенко . Вища математика,Київ,2002 р. . § 1.10

Після вивчення теми студенти повинні:

знати: поняття декартової системи координат; поняття вектора та векторного простору, базису векторного простору.

вміти: виконувати дії над векторами, заданими в координатній формі, знаходити скалярний добуток векторів, кут між векторами, довжину вектора;

розкладати вектори на лінійну комбінацію базисних векторів; визначати лінійну залежність і незалежність векторів.

Питання для самоперевірки

1. Що таке вектор, які види векторів ви знаєте?

2. В чому полягає геометрична інтерпретація вектора? Що таке напрямні косинуси?

3. Які вектори утворюють базис?

4. Як визначити лінійну залежність і незалежність векторів?

5. Перевірити, чи наведені нижче вектори лінійно незалежні і чи утворюють вони базис простору:

, , ;

, , , .

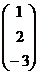Тема 6. Пряма лінія на площині. Рівняння прямої.

Мета: Закріпити поняття рівняння лінії на площині, навчитися виводити різні типи рівнянь на площині.