Варіант № 1. Варіант № 2. Варіант № 3

Варіант № 1

1. Основа прямої трикутної призми — прямокутний трикутник з катетами 3 см і 4 см. Висота призми 10 см. Знайдіть площу повної поверхні та об'єм призми.

2. Управильній чотирикутній піраміді бічне ребро довжиною 5 см утворює з площиною основи кут 45°. Знайдіть об’єм піраміди.

3. Відрізок, що сполучає центр верхньої основи з точкою кола нижньої основи, дорівнює 6 см. Знайдіть об’єм циліндра, якщо його висота дорівнює діаметру основи.

4.Осьовим перерізом конуса є рівносторонній трикутник. Твірна конуса - 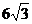см. Знайдіть об’єм конуса.

Варіант № 2

1. Основа прямої трикутної призми — прямокутний трикутник з катетом 5 см і гіпотенузою 13 см. Висота призми — 8 см. Знайдіть площу повної поверхні та об'єм призми

2.Висота правильної трикутної піраміди дорівнює 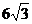см. Сторона основи піраміди — 4 см. Знайдіть площу бічної поверхні і об’єм піраміди.

3. Діагональ осьового перерізу циліндра дорівнює 12 см. Знайдіть об’єм циліндра, якщо його висота дорівнює діаметру основи.

4. Твірна конуса дорівнює 14 см. Кут при вершині осьового перерізу - 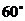. Знайдіть площу поверхні та об’єм конуса.

Варіант № 3

1. Знайдіть площу повної поверхні та об'єм прямокутного паралелепіпеда, якщо сторони основ 2 см і 3 см., а діагоналі паралелепіпеда - 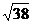см.

2. Сторона основи правильної чотирикутної піраміди 9 см, а бічне ребро 6 см Знайдіть об’єм піраміди та площу бічної поверхні.

3. Висота циліндра дорівнює 5 см, а діагональ осьового перерізу – 13 см. Знайдіть об’єм циліндра.

4. У конусі висота дорівнює 20 см, а відстань від основи висоти до твірної – 12 см. Знайдіть об’єм і площу поверхні конуса.

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒