Задача 54. Задача 55

Задача 54

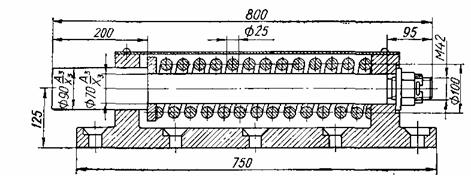
Гружёная тележка массой 42000 кг останавливается, ударяясь в два неподвижных буфера, показанных на рисунке. Допускаемое касательное напряжение в витках пружин [t] =500МПа. Пружина имеет 12 рабочих витков и предварительно подтянута на 10мм. Наименьший зазор между витками 3мм. Индекс пружины с = D/d = 100:25 =4, поправочный коэффициент k=1.38. Модуль упругости материала проволоки G =8*10⁴МПа.

Определить допускаемую скорость тележки в момент удара и вычислить высоту пружины в свободном состоянии.

Порядок решения:

Допускаемое продольное усилие в пружине (см. решение задачи 53)

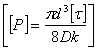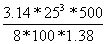= =22220Н.

Осадка пружины .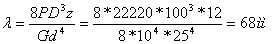

Жёсткость пружины С =P/l = 22220/68 =326,8 Н/мм.

Согласно условию задачи предварительная деформация пружины l₀ =10мм.

При изменении деформации от l₀ до l каждая из двух пружин поглощает половину кинетической энергии тележки, т.е. работа сжатия пружин уменьшает кинетическую энергию тележки до нуля. Обозначив массу тележки- mи скорость её движения - ν, пренебрегая потерями на трение, получим равенство 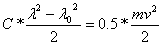, откуда

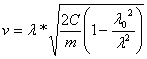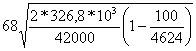= =265мм/с =15,9м/мин.

При заданном наименьшем зазоре между витками 3мм необходимая в свободном состоянии высота пружины H = z(d+3) +d +l = 12*(23+3) +25 +68 =430мм.

Задача 55

Спроектировать цилиндрическую пружину кручения из проволоки круглого сечения. Максимальный момент М_к = 5000Нмм, необходимый угол закручивания a=180⁰, допускаемое напряжение изгиба материала проволоки [s_и] =500МПа, индекс пружины c =D/d =8 , (где d – диаметр проволоки, D – средний диаметр пружины). Модуль упругости материала пружины Е = 2*10⁵МПа. Коэффициент, учитывающий кривизну прутка вычислить по формуле .

Порядок решения:

При нагружении пружины в каждом её сечении действует момент М, равный внешнему закручивающему моменту. Этот момент направлен вдоль оси пружины и раскладывается на момент М_и= М*Сosa - изгибающий виток и крутящий момент М_к= М*Sina (a- угол подъёма витка). При расчёте пружины на кручение нас интересует напряжение изгиба, которое получается от закручивания и вычисляется по формуле , где 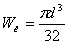- момент сопротивления изгибу сечения проволоки, 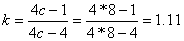- коэффициент учитывающий кривизну прутка. Подставляя значения, получим требуемый диаметр проволоки

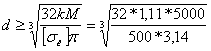= 4,8мм. Принимаем проволоку диаметром 5мм.

Средний диаметр пружины D =c*d =8*5 =40мм.

Угол закручивания пружины (рад) может быть определён как угол взаимного упругого наклона концевых сечений бруса длиной L, ( равной суммарной длине витков пружины), под действием чистого изгиба

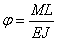, где L =p*D*z - длина пружины, J= 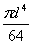- момент инерции сечения проволоки, z – рабочее число витков пружины. Преобразовывая угол закручивания в градусы, определяем необходимое количество витков пружины

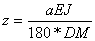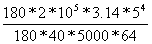= =31,2

Шаг витков пружины t = d + 0.5мм = 5,5мм.

Высота пружины из принимаемого зазора между витками 0,5мм,

Н = z*(d+0.5) =31*5.5 = 170,5 мм.

⇐ Предыдущая 11 12 13 14 15 16 17 181920 Следующая ⇒