
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача 51
Задача 51
 Р
Р
l
40мм
2000Н
 Спроектировать цилиндрическую пружину сжатия из проволоки круглого сечения. Характеристика пружины (зависимость осадки l от нагрузки) показана на рисунке. Индекс пружины с= D/d =5; Модуль сдвига материала проволоки G=8*104 МПа;
Спроектировать цилиндрическую пружину сжатия из проволоки круглого сечения. Характеристика пружины (зависимость осадки l от нагрузки) показана на рисунке. Индекс пружины с= D/d =5; Модуль сдвига материала проволоки G=8*104 МПа;
Допускаемое напряжение на кручение материала проволоки [t]=230МПа; значение поправочного коэффициента k принять из таблицы.
| C | |||||||
| k | 1.42 | 1.31 | 1.25 | 1.21 | 1.18 | 1.16 | 1.14 |
Порядок решения:
Напряжения в витках пружины вычисляются исходя из момента закручивания проволоки T = P / 0.5D. Полярный момент сопротивления прутка круглого сечения 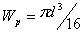 . Отсюда напряжение кручения в витках пружины
. Отсюда напряжение кручения в витках пружины 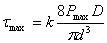 или
или 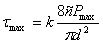 , где k – коэффициент, учитывающий кривизну витков и влияние поперечной силы в зависимости от индекса пружины с =D/d.
, где k – коэффициент, учитывающий кривизну витков и влияние поперечной силы в зависимости от индекса пружины с =D/d.
Принимая k= 1.3, при с=5 (см. таблицу) получим  =12мм.
=12мм.
Диаметр пружины D =c*d = 60мм.
Осадка пружины 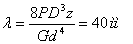 , отсюда необходимое число рабочих витков
, отсюда необходимое число рабочих витков 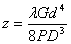 =19,2.
=19,2.
Полное число витков zп =z+(1.5-2) =21
Минимальный зазор между витками пружины при полной нагрузке 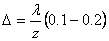 = 0,3мм
= 0,3мм
Шаг пружины при максимальной нагрузке 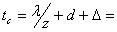 14,4мм.
14,4мм.
Длина пружины, сжатой до соприкосновения витков L = (zп –0.5)d = 246мм.
Длина ненагруженной пружины L0 = L+z(tс - d) = 292мм.
Длина пружины под нагрузкой равной P L1 = L0 - l =252мм.
Шаг ненагруженной пружины 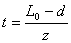 =14,6мм.
=14,6мм.
Длина проволоки для изготовления пружины 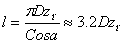 =4032мм.
=4032мм.
 Задача 52
Задача 52
40мм
Р
l
200Н
 Спроектировать цилиндрическую пружину растяжения из проволоки круглого сечения. Характеристика пружины (зависимость осадки l от нагрузки) показана на рисунке. Индекс пружины с= D/d =4; Модуль сдвига материала проволоки G=8*104 МПа;
Спроектировать цилиндрическую пружину растяжения из проволоки круглого сечения. Характеристика пружины (зависимость осадки l от нагрузки) показана на рисунке. Индекс пружины с= D/d =4; Модуль сдвига материала проволоки G=8*104 МПа;
Допускаемое напряжение на кручение материала проволоки
[t]=240МПа; значение поправочного коэффициента k принять из таблицы.
| C | |||||||
| k | 1.42 | 1.31 | 1.25 | 1.21 | 1.18 | 1.16 | 1.14 |
Порядок решения:
Напряжения в витках пружины вычисляются исходя из момента закручивания проволоки T = P / 0.5D. Полярный момент сопротивления прутка круглого сечения 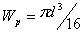 . Отсюда напряжение кручения в витках пружины
. Отсюда напряжение кручения в витках пружины 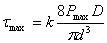 или
или 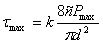 , где k – коэффициент, учитывающий кривизну витков и влияние поперечной силы в зависимости от индекса пружины с =D/d.
, где k – коэффициент, учитывающий кривизну витков и влияние поперечной силы в зависимости от индекса пружины с =D/d.
Принимая k= 1.42, при с=4 (см. таблицу) получим  =3,5мм.
=3,5мм.
Диаметр пружины D =c*d = 14мм.
Осадка пружины 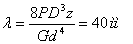 , отсюда необходимое число рабочих витков
, отсюда необходимое число рабочих витков
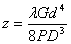 =109,5.
=109,5.
Шаг пружины t = d = 3.5мм.
Полное число витков zп =z + (0.5-1)d = 110
Длина пружины в свободном состоянии L0 =(zп +1)d = 388.5мм.
Длина пружины в свободном состоянии с зацепами L = L0 + 2hпр =428мм.
Длина зацепа hпр =(1-2)D =20мм.
Длина пружины при максимальной деформации Lmax = L + l = 468мм.
 Задача 53
Задача 53
Две пружины вставлены одна в другую. До приложения к плите сила Р = 1200Н вторая пружина короче первой на d = 20мм. Найти наибольшие касательные напряжения tmax и вычислить перемещение плиты при следующих условиях:
Средние диаметры пружин равны соответственно D1 =200мм, D2 = 100мм. Диаметры проволоки пружин d1 =20мм, d2 = 10мм. Число витков z1 =15,
z2 =10.
Модуль сдвига материала проволоки G =8*104МПа.
Коэффициент приведения k в зависимости от индекса пружины c= D/d принять по таблице
Порядок решения:
Если при рабочей нагрузке плита опустится на величину меньшую или равную d, то сжиматься будет лишь большая пружина, и задача в этом случае статически определима. Если перемещение плиты больше d, то сжимаются обе пружины и система статически не определима. Выясним прежде всего характер работы данной системы: найдём силу Р0, необходимую для сжатия первой пружины на d =20мм и сопоставим эту силу с заданной.
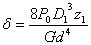 (cм. решение задачи 52), откуда
(cм. решение задачи 52), откуда 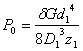 = 534Н.
= 534Н.
Следовательно при действии силы Р =1200Н нагружены обе пружины. При этом осадка первой пружины l1 на d больше осадки второй пружины l2.
Уравнение перемещений l1 - l2 =d = 20мм.
Уравнение равновесия сил Р1 + Р2 = Р =1200Н, или Р1 = 1200Н – Р2.
Совместное решение данных уравнений даёт: Р1 =800Н, Р2 = 400Н.
Определяем максимальные касательные напряжения в пружинах
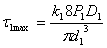 = 58МПа, где k1 = 1.14 (по таблице при с = 10)
= 58МПа, где k1 = 1.14 (по таблице при с = 10)
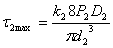 =116МПа, где k2 = 1.14 (по таблице при с = 10).
=116МПа, где k2 = 1.14 (по таблице при с = 10).
Определяем перемещение плиты, равное осадке первой пружины
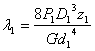 = 60мм.
= 60мм.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|