Подбор сечения по условиям безопасной устойчивости

13.4. Подбор сечения по условиям безопасной устойчивости

Условие устойчивости равновесия записывается либо в напряжениях: σ≤ σ_s _adm , либо в нагрузках: F ≤ F_s _adm , где σ_s _adm и F_s _adm – допускаемые напряжение и нагрузка по условиям безопасной устойчивости; при этом

σ_{s adm} = σ_cr/ n_s, F_{s adm} = F_cr/ n_s,

где n_s –коэффициент запаса устойчивости, который равен или превосходит коэффициент запаса прочности n (отклонения от проекта конструкции в отношении формы стержня, линии действия нагрузки уменьшают критическую нагрузку и σ_cr , но почти не влияют на прочность конструкции).

Исходя из использования сопротивления системы в целом, принимают условия устойчивости равновесия в нагрузках. В отдельных случаях это равнозначно принятию условия устойчивости равновесия в напряжениях. Для центрально сжатой стойки допустимая нагрузка

F_{s adm} = (π²EI_min)/(μ²l²n_s),

откуда при заданных значениях n_s, E, l и вычисленном значении μ можно найти I_min. Рациональным считается сечение, у которого I_min = I_max(при μ_y = μ_z).

Установим связь между допускаемым напряжением на устойчивость и величиной σ_adm:

σ_s _adm /σ_adm = (σ_cr n)/( σ_b n_s) = φ.

Учитывая, что σ_cr < σ_b, а n ≤ n_s устанавливаем, чтоφ<1. Величина φесть коэффициент уменьшения основного допускаемого напряжения для сжатых стержней (коэффициент продольного изгибa). Имея зависимость σ_cr~ λ для данного материала, зная σ_adm и выбрав n_s, можно составить таблицы значений φ в функции от гибкости λ.

В связи с зависимостьюφ от формы и размеров сечения подбор сечения по условиям устойчивости σ ≤ φσ_adm ведется путем последовательных прибли-жений. Выбираем форму сечения и задаемся его размерами (или при-мерным значением φ, например, φ₁= 0,5); вычисляем наименьший радиус инерции и гибкость; находим по таблице коэффициент φ₁' и вычисляем σ_s _adm = φ₁' σ_adm; сравниваем действительное напряжение σ с полученной величиной σ_s _adm; если условие устойчивости не удовлетворено или удовлетворено с большим запасом (разница между σ и σ_s _adm не должна превышать 3 – 5%), меняем размеры сече-ния (задаемся новым значением φ₂, равным среднему арифметическому величин φ₁ и φ₁') и повторяем расчет. Окончательно выбранное сечение должно удовлетворять и условию прочности: σ ≤ σ_adm.

13.5 Продольно поперечный изгиб сжатых стержней.

Если на массивный элемент одновременно действуют сжимающая сила и поперечные нагрузки, то напряжения определяют на основании принципа неза-висимости действия сил, суммируя алгебраически составляющие от каждого вида нагрузки.

Для гибких стержней такой метод расчёта неприемлем, так как сжимаю-щая сила за счёт существования значительных прогибов вызывает в стержне не только равномерное сжатие, но дополнительные изгибающие моменты, соизме-римые с моментами от поперечных сил. Расчёт проводят по деформированной схеме. Поскольку поперечный изгиб сопровождается и изгибом от продольных сил, то этот расчёт ещё называют продольно- поперечным изгибом.

Изгибающий момент в по- перечном сечении стержня (рис. 13.6) при продольно- поперечном изгибе можно представить в виде

М=М_о+FV

где: М_о- изгибающий момент вы-зываемый только поперечной нагрузкой S.

Суммарный момент М можно определить зная прогиб V, а последний в свою очередь зависит от момента.

Если кривизна оси стержня достаточно мала, то уравнение равновесия запишется так:

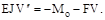
Решение должно выполнятся индивидуально для каждой схемы нагруже-ния. Оно значительно усложняется, если участков несколько.

Представим прогиб в виде суммы

V=V_o=ΔV,

где: V_o- прогиб, вызванный только поперечной нагрузкой;

ΔV- дополнительный прогиб, появившийся в результате действия сжимающей силы F.

Для прогиба V_o справедливо уравнение

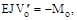(а)

следовательно

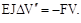(б)

Сделаем предположение, что дополнительный прогиб ΔV изменяется по закону синусоиды

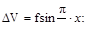
тогда

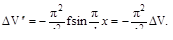(в)

Поскольку

ΔV=V-V_o (см. (а)) и 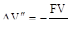(из ур. (б)),

то ,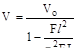

или

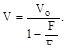
Допущения о синусоидальности изменения ΔV хорошо согласуется для стержня, имеющего шарнирное закрепление опор. Для других схем закрепле-ния концов стержня следует определить F_э каждый раз с учётом закрепления по формуле

где: J- момент инерции относительно главной центральной оси, соответствую-щей изгибу в данной плоскости;

μ- коэффициент приведения длины.

Величину V_o можно определить любым известным способом, после чего определяют V, а затем и напряжения в соответствующем сечении.

При решении задач на продольно - поперечный изгиб необходимо на-чать расчёт с проверки на устойчивость в плоскости наименьшей жёсткости

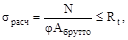
и если она удовлетворяется, переходят к дальнейшему расчёту.

Наибольшие (сжимающие ) напряжения определяются выражением

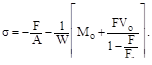
Поскольку напряжения нелинейно связаны с величиной силы F, то по величине напряжений нельзя судить о том, какой запас прочности имеется при заданной нагрузке. Из графика (рис. 13.7) видно, что напряжения в большей степени отличаются друг от друга, чем силы, их вызывавшие. Напряжения растут более интен-сивно, чем сжимающая сила. Это главное отличие работы гибких стержней при продольно попереч-ном изгибе.

Оценку запаса прочности следует проводить по величине отношения

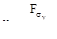
Рис. 13.7 где: 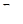- сила вызывающая напряжение, соответствующие пределу текучести; F- действующая нагрузка.

⇐ Предыдущая 49 50 51 52 535455 56 57 58 Следующая ⇒