
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практикум. Примеры
7.6 Практикум
Примеры
1. Для стального бруса (Е=2 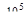 МПа) построить эпюры продольных сил, нор-
МПа) построить эпюры продольных сил, нор-
мальных напряжений в поперечных сечениях бруса и перемещения этих сече-
ние.
 Решение. Продольную силу в поперечном сечении определим проектируя внешние силы, приложенные справа от рассматриваемого сечения на ось бруса:
Решение. Продольную силу в поперечном сечении определим проектируя внешние силы, приложенные справа от рассматриваемого сечения на ось бруса:
NDL=0; NBC=60 кH;
NAB=60+120=180 кH.
По полученным значениям строим эпюру продольных сил N (рис.б)
В поперечных сечениях бруса воз-никают нормальные напряжения.
σDL= 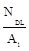 =0;
=0;
σCD= 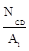 =
= 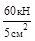 =
= 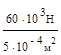 =
=
=12 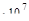 Па=120 МПа;
Па=120 МПа;
σВС= 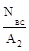 =
=  = 50 МПа; σАВ=
= 50 МПа; σАВ= 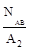 =
= 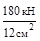 = 150 МПа.
= 150 МПа.
По полученным значениям строим эпюру нормальных напряжений σ (рис.в).
Поперечные сечения бруса под действием внешних сил смещаются впра-во относительно неподвижного сечения А. Величина  смещения сечения, ра- положенного на расстоянии х от левого конца бруса равна деформации уча-стка длинной х:
смещения сечения, ра- положенного на расстоянии х от левого конца бруса равна деформации уча-стка длинной х:
на участке АВ при (0  )
)
 АВ=
АВ= 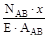 =
= 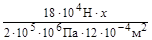 =0.75
=0.75 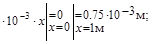
на участке ВС при (0 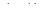 )
)
 ВС=
ВС= 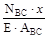 =0.75
=0.75 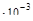 +
+ 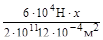
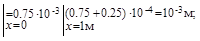
на участке АВ при (0 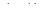 )
)
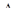 CD=
CD= 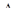 ВС +
ВС + 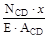 =103+
=103+ 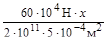 =
= 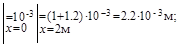
Участок DL не деформируется (NDL=0, следовательно 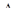 DL=0), но пере-мещается в следствии деформаций участков, расположенных слева.
DL=0), но пере-мещается в следствии деформаций участков, расположенных слева.
Во всех полученных выражениях переменная х входит в первой степени, а следовательно зависимость между  и х линейная. Это позволяет по расчётным перемещениям сечений В, С, D, L построить эпюру перемещений
и х линейная. Это позволяет по расчётным перемещениям сечений В, С, D, L построить эпюру перемещений  (в размерности мм).
(в размерности мм).
Поскольку  I=
I= 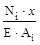 =
= 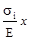 =εi·х, то относительная продольная деформация εi на каждом участке представляет собой коэффициент, соответ-ствующий углу наклона эпюры
=εi·х, то относительная продольная деформация εi на каждом участке представляет собой коэффициент, соответ-ствующий углу наклона эпюры  на каждом участке. Сравнивая эпюры σ и эпюры
на каждом участке. Сравнивая эпюры σ и эпюры  можно наблюдать, что чем больше значения σ, тем круче линия эпюры
можно наблюдать, что чем больше значения σ, тем круче линия эпюры  (при условии Е=const), а на участке DL – эпюра перемещений гори-зонтальна.
(при условии Е=const), а на участке DL – эпюра перемещений гори-зонтальна.
 2. Для металлического бруса, находящегося под действием сил построена эпюра N продольных сил, возника-ющих в его сечениях. Произвести расчёт на прочность стержня в следующих случаях.
2. Для металлического бруса, находящегося под действием сил построена эпюра N продольных сил, возника-ющих в его сечениях. Произвести расчёт на прочность стержня в следующих случаях.
2.1 Стержень изготовлен из плас-тичной стали:
σadm=160 МПа, F=40 кН. Подобрать площади поперечных сечений для каждого из участков.
Решение. Условие безопасной прочности σ = 
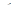 σadm позволяет вычислить минимальную площадь поперечного сечения:
σadm позволяет вычислить минимальную площадь поперечного сечения:
А1 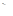
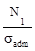 =
= 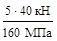 =
= 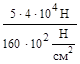 =12.5 см2;
=12.5 см2;
А2 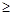
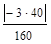 = 7.5 см2; А3
= 7.5 см2; А3 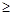
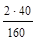 = 5 см2.
= 5 см2.
Для второго участка, где N2 <0 берём абсолютное значение силы 120 кН и делим на допускаемое напряжение σadm=160 МПа, которое для пластичных ма-
териалов имеет одинаковое значение и в случае растяжения, и в случае сжатия. Принимаем: А1=12.5 см2; А2=7.5 см2; А3=5 см2.
2.2 Стержень изготовлен из чугуна:
σadmр=120 МПа; σadmс=310 МПа; F=50 кН; А1=25 см2; А2 =; А3= ?
Проверить прочность стержня. Дать рекомендации по изменению поперечных сечений (рациональные сечения).
Решение. Определим напряжения на каждом участке
σ1 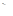
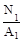 =
= 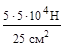 =104
=104 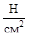 =100 МПа; σ2=
=100 МПа; σ2= 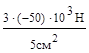 = -300 МПа;
= -300 МПа;
σ3= 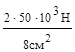 = 125 МПа. Условия безопасности прочности на первом участ-ке σ1=100 МПа
= 125 МПа. Условия безопасности прочности на первом участ-ке σ1=100 МПа 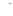 120 МПа = σadm выполняется, но площадь этого участка мож-но уменьшить до величины
120 МПа = σadm выполняется, но площадь этого участка мож-но уменьшить до величины 
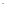
 = 20.83 см3 (принимаем 21см2), тогда потребуется меньше материала для изготовления конструкции.
= 20.83 см3 (принимаем 21см2), тогда потребуется меньше материала для изготовления конструкции.
На втором участке σ2= 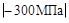
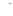 310 МПа = σadmс сравнивать необходимо абсолютную величину сжимающих напряжений. Условие прочности выполне-но, а недонапряжение
310 МПа = σadmс сравнивать необходимо абсолютную величину сжимающих напряжений. Условие прочности выполне-но, а недонапряжение  σ%=
σ%= 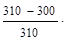 100%
100% 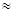 3.2%
3.2%
На третьем участке σ3=125 МПа 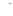 120 МПа=σadm, и условие формально не выполняется. Однако перегрузка
120 МПа=σadm, и условие формально не выполняется. Однако перегрузка 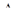 σ%=
σ%= 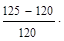 100%
100% 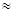 4.2% не превышает 5%, что позволяет оставить площадь третьего участка А3=8 см2.
4.2% не превышает 5%, что позволяет оставить площадь третьего участка А3=8 см2.
2.3 Стержень изготовлен из пластичной стали:
σadm=160 МПа; А1=30 см2; А2=15 см2; А3=20 см2. Определить допускаемое зна-чение нагрузки F.
Решение. Следует сравнить напряжения на каждом из трёх участков и из усло-вия безопасной прочности σмах= 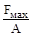
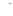 σadm, определить величину допускае-мой силы F.
σadm, определить величину допускае-мой силы F.
σ 1 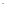
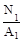 =
= 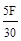 = 0.167 F; σ 2
= 0.167 F; σ 2 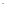
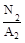 =
= 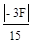 =0.2 F; σ 3
=0.2 F; σ 3 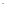
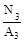 =
= 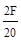 = 0.1 F.
= 0.1 F.
На втором участке нормальные напряжения наибольшие по абсолютному зна-чению, поэтому, наибольшее значение силы Fмах.
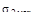
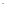
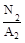 =
= 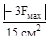 ≤ 160 МПа = σadm Fмах
≤ 160 МПа = σadm Fмах 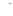 160
160 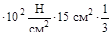 =
=
=8·104 Н = 80 кН. Допускаемая величина силы Fadm= 80 кН. При таком значении силы на втором участке нормальные напряжения равны σadm, а на первом и втором участке они соответственно составляют 83.5% и 50% от σadm.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|