СДВИГ. Основные положения

8. СДВИГ

8.1 Основные положения

Исследуя в п.4.2 плоское напряженное состояние, мы установили, что если главные напряжения равны по величине и противоположны по знаку, то площадки, наклоненные к главным под углом 45°, являются площадками чистого сдвига (рис. 8.1).

Чистый сдвиг прямоугольного призматического бруса вызывается поперечными силами по четырем его граням. На рис. 8.2 показан чистый сдвиг в плоскости ху. Зададим следующие условия: 1) отсутствуют линейные деформации, а следовательно, нормальные напряжения и соответствующие им внутренние усилия в поперечных сечениях бруса (продольная сила и изгибающие моменты); 2) отсутствует деформация сдвига γ_zx , а следовательно, τ_zx =τ_xz = 0, Q_z= 0; 3) сечение остается плоским, т.е. γ_xy = const; 4) физический закон − закон Гука при сдвиге; из него вытекает, что τ_yx = τ_xy = const; как следствие, крутящий момент при совмещении центра приведения с центром тяжести обращается в нуль; 5) задана величина поперечной силы Q_y.

Рис. 8.1 Рис. 8.2

Для определения напряжений, деформаций и перемещений привлекаем зависимости по трем законам деформирования для τ_xy и γ_xy:

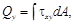γ_xy= ∂u/∂y+∂v/∂x, τ_xy=G γ_xy.

За основное неизвестное принимаем деформацию сдвига γ_xy. При малых величинах γ_xy можно пренебречь перемещениями v и принять γ_xy=∂u/∂y. Так как u – функция одной переменной у, то

γ_xy=du/dy,

откуда

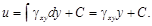
Из условия неподвижности нижней грани (u = 0 при y = 0) вытекает С = 0, и следовательно,

u = γ_xyy.

Интегральное уравнение при τ_xy = const принимает вид

Q_y = τ_xy A,

откуда

τ_xy = Q_y/A.

Обращаясь к физическому закону, находим

γ_xy = Q_y / (GA),

и окончательное выражение для перемещений

u = (Q_yy) / (GA).

Анализируя полученное решение, проведем некоторые параллели между сдвигом и растяжением (сжатием):

1. На торцах на основании статического граничного условия постоянное напряжение трансформируется в равномерно распределенную нагрузку Y_P = τ_xy, которая и соответствует рассмотренной деформации чистого сдвига. На основании свойства парности касательных напряжений по двум взаимно перпендикулярным площадкам на соответствующих продольных гранях также имеет место равномерно распределенная нагрузка Х_P = τ_yx = τ_xy (в этом отличие сдвига от растяжения). Равнодействующие Q_x и Q_y связаны между собой соотношением Q_y / Q_x=h / l.

2. Напряжение τ_xy прямо пропорционально Q_y и обратно пропорционально А. Следовательно, при заданной поперечной силе напряжение можно уменьшить путем увеличения площади поперечного сечения.

3. Деформация сдвига обратно пропорциональна величине GA, называемой жесткостью при сдвиге.

8.2. Практические расчёты соединений, работающих на сдвиг.

Для многих соединений , таких как сварные , болтовые заклёпочные, работающих в сложных напряжённых состояниях оценка работоспособности может быть проведена простыми, но довольно надёжными расчё-тами на сдвиг.

Изучив начальную стадию разрушения
заклёпочного соединения (рис 8.3) можно

Рис. 8.3 наблюдать, что происходит срез тела заклё-

пки по плоскостям соприкосновения листов. Количество площадок среза nнаединицу меньше числа соединяемых листов и пропорционально суммарному числу заклёпок в соединении k.

А_ср= 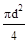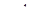, где d–диаметрзаклёпки.

Условия безопасности прочности

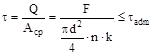если расчёт ведём по допускаемым напряжениям. При расчёте по предельным состояниям действующие напряжения среза τ сравнивают с расчётным сопротивлением материала заклёпки на срез R_ср. Так выполняют поверочный расчёт. При проектировании заклёпочного соединения диаметр заклёпки назначают, ориентируясь на толщину соединяемых пластин и из условия прочности определяют минимально возможное число заклёпок

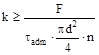
В заклёпочном соединении может происходить смятие отверстий листов по поверхности контакта. Это особенно важно при проектировании герметич-ных сосудов. В этом случае дополнительно выполняют проверку на смятие. До-полнительно следует проверить на растяжение и полосу, ослабленную отвер-стиями.

Расчёт болтовых соединений производят в том же порядке. Расчёт высо-копрочных болтов осуществляют из условия затяжки соединения необходимым моментом затяжки, обеспечивающим требуемое усилие на контактирующих поверхностях обжимаемых листов, на которых возникающие силы трения и во-спринимают срезающие усилия. Высокопрочный болт работает только на рас-тяжение. Площадь его поперечного сечения назначается из условия безо-пасной прочности на растяжение.

Сварные соединения менее трудоёмки в исполнении, не приводят к ос-лаблениям элементов, более экономичны. Сварные соединения, как и заклёпоч-ные, условно рассчитывают в предположении равномерного распределения напряжений по сечению шва.

Если сварное соединение довести до разрушения, то наплавленный мате-риал останется на обеих частях пластин (рис. 8.4 а).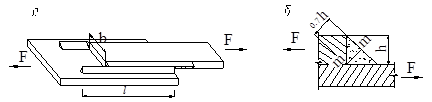

Рис. 8.4

Срез происходит по площадке m-m, площадке наименьшего сечения, размер которого составляет h 0.7 h, где h – высота катета углового шва. Ус-ловие безопасной прочности запишем в виде

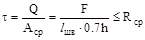где: R_ср – расчётное сопротивление материала сварного шва на срез;

l_шва – расчётная длина шва ( в нашем случае l_шва=2l).

Для случая когда дополнительно осуществить и сварку по торцу (лобовой шов) длиной b, l_шва=2l+b.

При проектировании соединения (рис. 8.5), называемого врубкой, следу-ет подобрать размеры площади abcdиз условия безопасной прочности матери-ала на скол (срез), а размеры площади cefb– из условия прочности на смятие (сжатие) от действия горизонтальной составляющей силы F.

Рис. 8.5

8.3 Практикум

⇐ Предыдущая 28 29 30 31 323334 35 36 37 Следующая ⇒