Поверочные и проектные расчеты

7.5. Поверочные и проектные расчеты

Смысл поверочного расчета по методу допускаемых напряжений состоит в сопоставлении фактических напряжений в опасном сечении бруса с допускаемыми:

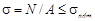Здесь и в дальнейших поверочных и проектных расчетах внутренние усилия берутся по модулю. Это неравенство называется условием безопасной прочности при растяжении (сжатии).

Фактические напряжения не должны отклоняться от допускаемых более, чем на 5%. Большее перенапряжение недопустимо с точки зрения безопасной прочности, а недонапряжение приводит к перерасходу материала.

Обратные задачи решаются при заданном допускаемом напряжении. В первом случае заданными считаются также размеры поперечного сечения, а определяется допускаемая продольная сила:

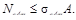
Во втором случае при известной нагрузке определяется площадь поперечного сечения

после чего вычисляют его размеры. Если их количество больше единицы, необходимы дополнительные соотношения между ними (например, отношение высоты прямоугольника к ширине).

Наиболее экономичным является брус равного сопротивления. Он имеет переменную по длине площадь поперечного сечения, подобранную так, что напряжения во всех сечениях одинаковы: σ_x = σ_adm.

Возьмем брус, подверженный растяжению силой F и собственным весом (рис. 7.4). Площадь нижнего сечения А₀ определяется из условия F/А₀= σ_adm:

A₀= F/ σ_adm.

Чтобы установить закон изменения площади сечения по высоте бруса, возьмем два смежных сечения. Приращение площади dA(x) при переходе от одного сечения к другому должно воспринять вес ρgA(x)dx элемента бруса между сече-ниями при том же напряжении:

Рис. 7.4

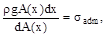
откуда

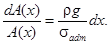
После интегрирования получаем

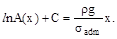
Подставим значение А(х) = А_о при х = 0:

ln А₀+ С = 0, и С =– ln A₀.

Окончательно

А(х) = A₀exp[(ρgx)/σ_adm] .

Криволинейность границы бруса удорожает его изготовление. На практике чаще применяют стержни ступенчатые или в виде усеченного конуса.

Приведенный проектный расчет является приближенным. Предполагалось, что по всему сечению бруса передаются только нормальные напряжения; на самом деле у краев сечения напряжения будут направлены по касательной к боковой поверхности.

Установлено, что формулу напряжений для бруса постоянного сечения можно применять с достаточной точностью для бруса переменного сечения, если угол конусности α ≤ 12º.

Важно заметить, что, рассматривая условия безопасной прочности, мы не предполагали отклонения от определенной начальной формы равновесия стержня. Эта проблема будет рассматриваться в гл. 13.

Помимо условия прочности, требуется выполнение условия жесткости:

N/(EA) ≤ ε_adm.

Решения обратных задач имеют вид:

N_adm≤ EA ε_adm , A ≥ N/( E ε_adm) , E ≥ N/( A ε_adm).

Легко заметить, что первые две формулы в случае совпадения величин Eε_adm и σ_adm будут тождественны соответствующим формулам, полученным из условия прочности, а в случае несовпадения –отличаться на постоянный множитель. Третья формула определяет новый тип проектной задачи – подбор материала с необходимыми упругими свойствами.

При расчете по предельным состояниям вместоσ_adm принимаются расчетныесопротивления растяжению(R_t) или сжатию (R_c).

⇐ Предыдущая 25 26 27 28 293031 32 33 34 Следующая ⇒