Напряженно-деформированное состояние круглого бруса

9.2. Напряженно-деформированное состояние круглого бруса

Для чистого кручения круглого цилиндрического бруса задаются следующие условия (используем цилиндрическую систему координат, см.рис.9.2): 1) в плоскости, касательной к цилиндрической поверхности, имеет место чистый сдвиг (γ_x_θ= const); 2) отсутствуют линейные деформации (ε_х = ε_ρ = ε_θ= 0), а следовательно, и нормальные напряжения и соответствующие им внутренние усилия в поперечных сечениях бруса (продольная сила и изгибающие моменты); 3) кривизна кручения в точках поперечного сечения сохраняет постоянное значение; 4) физический закон – закон Гука при сдвиге; 5) задан крутящий момент Т, Q_y = Q_x = 0. При заданных условиях по всей длине бруса соблюдается симметрия относительно оси х (осевая, круговая), заключающаяся в том, что при обходе в каждом сечении по дуге окружности угол сдвига γ_x_θ не меняет величину и направление. Значит, в точке ρ = 0 имеем γ_x_θ = 0, τ_x_θ = 0.

Для определения характеристик скручиваемого бруса k_t, γ_x_θ_,τ_x_θ и 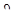привлекаем зависимости по трем законам деформирования:

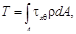
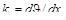
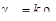
За основное неизвестное принимаем k_t. На основании двух последних зависимостей получаем τ_θ_x = Gγ_θ_x = Gk_tρ. По закону парности касательных напряжений τ_х_θ = τ_θ_x = Gk_tρ. Подставим это значение в интегральную формулу

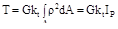откуда

k_t = T/(GI_Р) .

Следовательно,

γ_x_θ= (Tρ)/(GI_Р) , τ_х_θ = (Tρ)/ I_Р.

Наибольшее напряжение (на контуре сечения) равно

τ _{мах х}_K_t = (Тr)/I_Р = T/W_Р,

где W_Р - полярный момент сопротивления кругового сечения,

W_Р= (πr³)/2.

Дифференциальное уравнение углов закручивания имеет вид

d 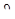/dx = T/(GI_P).

Его интеграл

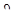= ∫[T/(GI_P)]dx + С = (Tx)/(GI_P) + С.

Из условия: при х = 0, 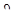= 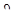(0) следует, что С = 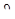(0), и следовательно,

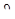= (Tx)/(GI_ρ) + 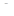(0).

Анализ полученного решения приводит к следующим выводам:

1. Кривизна кручения остается постоянной по длине бруса.

2. Напряжения τ_х_θ не меняют своего закона по длине бруса и являются функцией только координаты ρ. На торцах на основании статического граничного условия они трансформируются в распределенную линейно вдоль радиусов нагрузку, которая и соответствует рассмотренной деформации.

3. Кривизна кручения и деформация сдвига пропорциональны величине GI_P, называемой жесткостью при кручении.

⇐ Предыдущая 30 31 32 33 343536 37 38 39 Следующая ⇒