
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примеры. Вопросы для повторения. КРУЧЕНИЕ. Основные понятия
Примеры
1.Определить необходимое число заклёпок диаметром 1,2см для соединения “внахлёст” двух пластин толщиной 0,8см и шириной 10см, если известно, что нормальные напряжения в растянутой полосе σ =150МПа и τadm=100МПа.
Решение. Если в растянутой пластине напряжения известны, то вызывавшая их сила N=σ 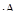 =150МПа
=150МПа 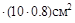 =1.5
=1.5  =120кН.
=120кН.
Эта сила будет срезающей для односрезных заклёпок, число которых:
k 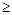
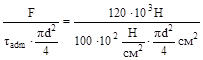 =10.6
=10.6
Число заклёпок для обеспечения безопасной прочности соединения должно быть не менее 11 шт.
2. Найти необходимую длину фланговых швов, соединяющих равнополочный уголок 63 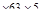 с пластиной если действующее срезающее усилие F=65кН, приняв Rср=96 МПа.
с пластиной если действующее срезающее усилие F=65кН, приняв Rср=96 МПа.
Решение. Условия безопасной прочности имеет вид:
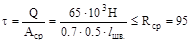 МПа (где h = 0.5см - толщина полки уголка)
МПа (где h = 0.5см - толщина полки уголка)
lшв 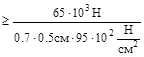 =19.5см.
=19.5см.
 Для обеспечения одинаковой работы левого и правого швов длины провара следует выбрать обратными расстояниям до центра тяжести сечения уголка от левого и правого шва
Для обеспечения одинаковой работы левого и правого швов длины провара следует выбрать обратными расстояниям до центра тяжести сечения уголка от левого и правого шва
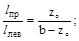
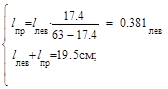
тогда lлев=14см, lпр=5.5см.
3. Две тяги соединены штырём, вставленным в проушины, и нагружены силой F=150кH. Определить действительный запас прочности, если: σу=230МПа; τу=180МПа.
Решение. Определим действующие напряжения среза в штыре
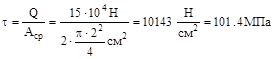
Запас прочности по касательным напряже-ниям 
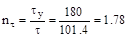
Определим действующие нормальные напря-жения в ослабленном сечении правой пласти-ны (т.к. суммарная толщина двух левых боль-ше и там напряжения меньше)
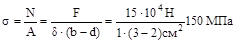 .
.
Запас прочности по нормальным напряжениям 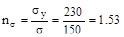 . Решением является 1.53 - меньший из двух.
. Решением является 1.53 - меньший из двух.
4. Пуансон диаметром 2см прошивает отверстие в стальной пластине толщиной 0.6см с усилием 130кН. Определить касательные напряжения в пластине и нор-мальные сжимающие напряжения в пуансоне.
Решение. Площадь среза представляет собой цилиндрическую поверхность ди-аметром 2см и высотой 0.6см. Аср= π 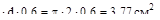
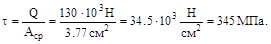
Напряжение в пуансоне 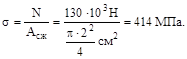
Вопросы для повторения
1.Какой случай плоского напряженного состояния называется чистым сдвигом?
2. Как записывается закон Гука при сдвиге?
3. Какие константы упругости для изотропного материала вам известны?
4. Как связаны эти константы?
5. В чём состоит закон парности касательных напряжений?
6. Как определяют величину τadm?
7. Какие упрощающие гипотезы используют при расчёте на срез?
8. Как связаны поперечная сила Q и касательные напряжения в площадке среза?
9. Как вычисляются действующие касательные напряжения в предполо-жении их равномерного распределения в сечении?
10. Запишите условие безопасной прочности при срезе.
11. Как определить действительный запас прочности, если известны дей-ствующие касательные напряжения и прочностные характеристики материала?
12. Как определить необходимое количество заклёпок, обеспечивающее безопасную прочность соединения?
13. Почему в условии прочности для сварного шва содержится множитель 0.7 катета шва?
14. Какие дополнительные проверки на прочность выполняют при расчёте заклёпочного соединения?
15. Как определяют число срезов заклёпки, соединяющих пакет из m ли-стов?
16. Почему при расчёте сварного соединения можно суммировать длины продольных и поперечных швов?
Тесты для повторения
1. Почему продольные (фланговые) швы предпочтительнее торцевых (лобовых) при ударных нагрузках?
(а) их можно выполнить более качественно;
(б) протяжённость таких швов неограниченна шириной полосы;
(в) потому что фланговые швы разрушаются без значительных пластических деформаций;
(г) фланговые швы разрушаются с образованием значительных пластических деформаций.
Ответ: (г), предшествующие разрушению значительные пластические деформации могут поглощать значительно большую энергию удара, а при разрушении лобовых швов абсолютные сдвиговые деформации малы.
2. Почему в заклёпочном соединении при большом количестве заклёпок их располагают несколькими рядами, а не в один ряд?
(а) заклёпки более равномерно нагружены;
(б) ослабление ”живого сечения” полосы меньше;
(в) все заклёпки не помещаются в один ряд;
(г) на каждую заклёпку в этом случае придётся большая часть нагрузки.
Ответ: (б), поскольку в этом случае ослабленная большим количеством отверстий под заклёпки полоса может не обеспечить прочность.
3. Если две пластины соединяются сваркой встык, а толщина пластины t и ширина b,то каким будет правильное условие прочности:
 (а)
(а) 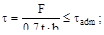 (б)
(б) 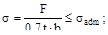
(в) 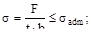 (г)
(г) 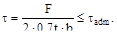
Ответ: (в), поскольку в таком сварном шве площадка разрушения (  ) и в ней действуют нормальные напряжения σ.
) и в ней действуют нормальные напряжения σ.
4. Две пластины соединены с помощью двух накладок и растянуты силой F. Катет шва h. Какая из формул будет верной при проверке на прочность?

(а) 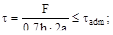 (б)
(б) 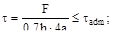
(в) 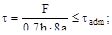 (г)
(г) 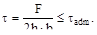
Ответ: (б), поскольку при разрушении соеди-нения образуются две части и общая длина разрушенного шва будет составлять 4а, и пло-щадь среза - 0.7ha.
9. КРУЧЕНИЕ
9.1. Основные понятия

Крутящие моменты T в поперечных сечениях бруса обычно возникают под действием внешних моментов Тe. Вращающийся стержень, подверженный преимущественно кручению, называется валом. Внешние моменты передаются на вал, как правило, в местах посадки на него шкивов, зубчатых колес и т.п. Если непосредственно вблизи от этих мест помещены опоры, то можно пренебречь сравнительно небольшим влиянием изгиба и рассчитывать вал только на кручение.
Рис. 9.1 Рис. 9.2
Для получения наглядного представления о деформации возьмем резиновый круглый цилиндрический брус с нанесенной прямоугольной сеткой, составленной семейством концентрических окружностей и образующими. Закрепим один конец и приложим к другому момент Тe (рис.9.1). Полученная в результате деформирования сетка из параллелограммов свидетельствует о величине сдвига. Окружности остаются неизменными, и расстояния между ними не меняются. На основании гипотезы плоских и жестких сечений (см. п. 7.1) каждое поперечное сечение поворачивается в своей плоскости на некоторый угол как жесткое целое. Радиусы всех сечений будут поворачиваться, оставаясь прямолинейными. Тем самым можно предположить, что характер деформаций, наблюдаемых на поверхности, будет таким же и внутри бруса на любой цилиндрической поверхности, концентричной с наружной.
Для установления геометрических соотношений рассмотрим элемент бруса (см. рис. 9.1) между сечениями I-I и II-II (сечение I-I условно закреплено) и сконцентрируем внимание на линии АВ′ и радиусе OВ′, которые до деформации занимали положение АВ и OВ (рис. 9.2). Поворот образующей АВ связан с из-
менением положения радиуса OB. Угол d 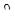 называется углом закручивания.
называется углом закручивания.
Перемещение точки С на радиусе ОВ связано с поворотом образующей DC
цилиндра произвольного радиуса ρ. Сопоставим длину дуги СС′ из двух вычислений:
dx γθx = ρd 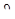 ,
,
откуда
γθx = (d 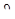 /dx)ρ.
/dx)ρ.
Относительный угол закручивания назовем кривизной кручения и обозначим kt. Таким образом, имеем
kt = d 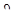 /dx , γθx = kt ρ.
/dx , γθx = kt ρ.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|