
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Искажение направления на наклонном снимке плоской местности
3.5.2. Искажение направления на наклонном снимке плоской местности
Влияние углов наклона снимка на направление будем анализировать при перенесении начала координат в главную точку снимка о. Выведем формулы связи координат точек снимка и местности в этом начале координат, и применим их к данному вопросу.
| O |
| a´´ |
| a´ |
| a |
| o |
| A |
| d |
| S |
| X |
| α |
| H |
| f |
| i |
| α |
| x |
Рис.3.8. Линейная перспектива с началом координат в точке o
Из соотношения подобия (рис.3.9)
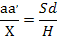
найдем
 (3.38)
(3.38)
Здесь
 (3.39)
(3.39)
Поскольку
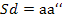
и
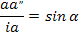
то
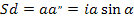
Отрезок ia находится как разность
s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 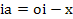 ,
,
причем
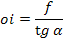
Тогда
 .
.
и
 (3.40)
(3.40)
После подстановки(3.39), (3.40) в (3.38) окончательно находим
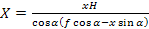 (3.41)
(3.41)
Выполняя аналогичные выводы по ординатам можно получить
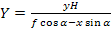 (3.42)
(3.42)
Вывод формулы влияния угла наклона снимка на направление
Выведенные формулы применим для анализа влияния угла наклона на направления.
Для горизонтального снимка при H=f можно записать


(3.43)
Условно будем считать, что направление проведено из центра снимка под углом φ к оси х(рис. 3.10)
| φφ |
| y |
| x |
| y |
| x |
Рис. 3.10. Направление на снимке
Можно записать очевидное соотношение
 ,
,
где 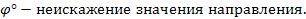
Искаженное значение равно
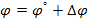 .
.
Исходя из выведенных формул (3.35) связи координат наклонного и горизонтального снимков запишем

или
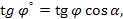
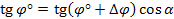 (3.44)
(3.44)
Разложим tg  в ряд Тейлора:
в ряд Тейлора:
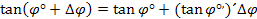
или
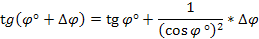
Тогда в соответствии с (3.44)
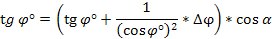
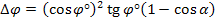
Полагая
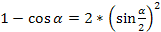 ,
,
Окончательно, обозначая d wsp:val="00FF5AF3"/><wsp:rsid wsp:val="00FF6362"/></wsp:rsids></w:docPr><w:body><w:p wsp:rsidR="00000000" wsp:rsidRDefault="004B48B6"><m:oMathPara><m:oMath><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>в?†П†</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 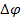 через Δφα найдем
через Δφα найдем
 (3.45)
(3.45)
Пример: Пусть d wsp:val="00FF5AF3"/><wsp:rsid wsp:val="00FF6362"/></wsp:rsids></w:docPr><w:body><w:p wsp:rsidR="00000000" wsp:rsidRDefault="006E55B4"><m:oMathPara><m:oMath><m:r><m:rPr><m:sty m:val="p"/></m:rPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/></w:rPr><m:t> П†В°=45В°</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 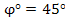 ,d wsp:val="00FF5AF3"/><wsp:rsid wsp:val="00FF6362"/></wsp:rsids></w:docPr><w:body><w:p wsp:rsidR="00000000" wsp:rsidRDefault="00FD7743"><m:oMathPara><m:oMath><m:r><m:rPr><m:sty m:val="p"/></m:rPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/></w:rPr><m:t>О±=3В°</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
,d wsp:val="00FF5AF3"/><wsp:rsid wsp:val="00FF6362"/></wsp:rsids></w:docPr><w:body><w:p wsp:rsidR="00000000" wsp:rsidRDefault="00FD7743"><m:oMathPara><m:oMath><m:r><m:rPr><m:sty m:val="p"/></m:rPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/></w:rPr><m:t>О±=3В°</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  . Тогда
. Тогда
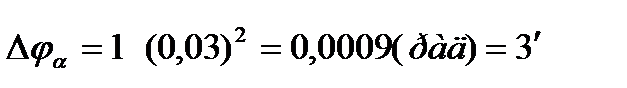 (3.46)
(3.46)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|