
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача 3.3. Решить обратную к задаче 3.1. По известным координатам точки местности вычислить соответствующие ей координаты на снимке. Исходными принять данные к задаче 3.1 и результаты ее решения.. Масштаб снимка
Задача 3.3. Решить обратную к задаче 3.1. По известным координатам точки местности вычислить соответствующие ей координаты на снимке. Исходными принять данные к задаче 3.1 и результаты ее решения.
3.4.Масштаб снимка
В общем случае масштаб снимка зависит от углов его наклона и рельефа местности. Однако исследование его масштаба в зависимости от одного угла наклона, например, от продольного – α, имеет также практический интерес. В этом случае можно определить допуски на углы наклона, при которых снимком можно пользоваться как горизонтальным и при которых такой снимок можно считать планом для тех или иных целей.
В случае одного угла наклона снимка центральная проекция имеет вид линейной перспективы (рис. 3.5)
| Y |
| T |
| o |
| O |
| c |
| C |
| n |
| N |
| α |
| α/2 |
| α |
| S |
| T |
| h |
| h |
| i |
| i |
| v |
| v |
| I |
| Q |
| P |
| E |
| H |
| X |
| x |
| f |
На рис.3.5 S – центр проекции или точка фотографирования,SO – главный луч, SO = f – фокусное расстояние, Н – высота фотографирования, Е – предметная плоскость, Р – плоскость снимка, О – главная точка снимка как пересечение главного луча со снимком, α – угол наклона снимка (в данном случае только продольный), ТТ – линия основания, Q – плоскость главного вертикала ( ее обозначают еще через W), υυ – главная вертикаль как пересечение плоскостей снимка и главного вертикала, hh – главная горизонталь, ii – линия истинного горизонта, I – главная точка схода, N,n – точки стояния (надира) на местности и на снимке.
Обозначая отрезок изображения на снимке через dl (рис.3.6)как элементарный отрезок, а ему соответствующий на местности - dL, запишем формулу масштаба изображения:
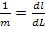 (3.20)
(3.20)
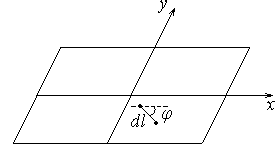
Рис. 3.6. Элементарный отрезок на снимке
Для придания выводам большей общности примем, что настоящий отрезок находится под углом 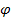 к оси x.
к оси x.
Для упрощения выводов формула (3.20) несколько изменяется:
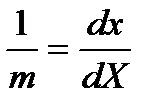 . (3.21)
. (3.21)
где dx, dX – дифференциалы координат точки на снимке и на местности
Поскольку
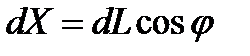
то
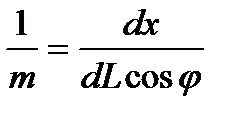
где
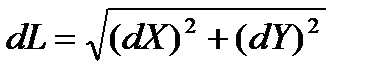 ,
,
а dX и dY -дифференциалы координат точки местности.
Выразим их через дифференциалы координат на снимке
Для этого воспользуемся формулами связи координат точек снимка и местности (3.5)
для частного случая, когда α=α, ω=0, κ=0
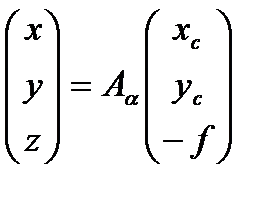 , или
, или
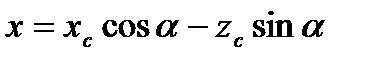 ,
,
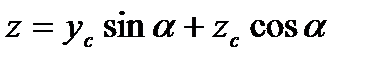
zc=-f,
Тогда
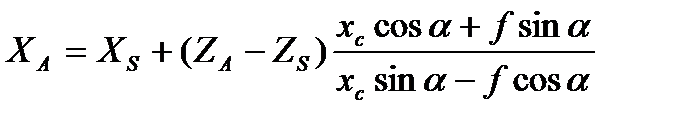 (3.22)
(3.22)
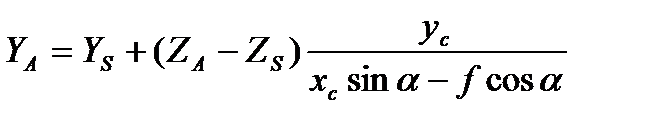 (3.23)
(3.23)
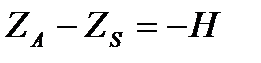 , где Н – высота фотографирования.
, где Н – высота фотографирования.
Для простоты дальнейшего изложения примем XS=YS=0, XA=X, YA=Y.
Тогда
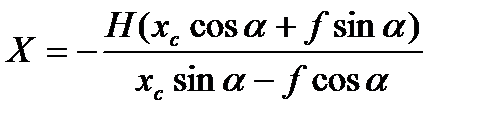 (3.24)
(3.24)
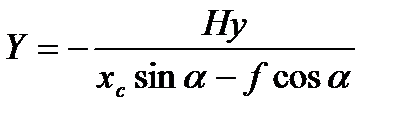 (3.25)
(3.25)
Найдем dX, dY
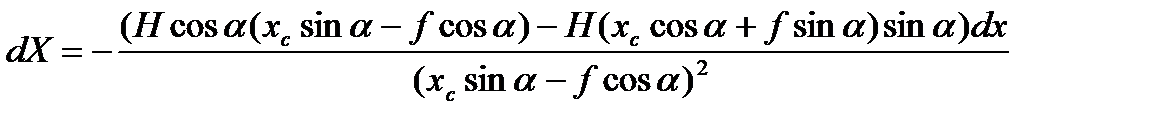
Раскроем скобки
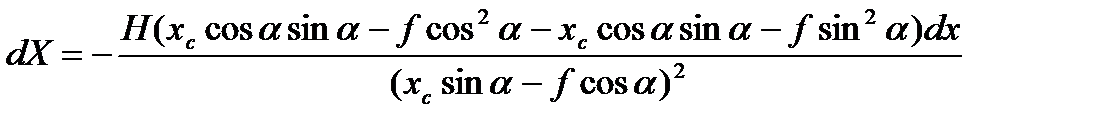 ,
,
и получим
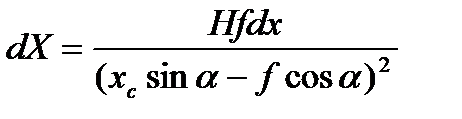
В учебниках по фотограмметрии эта формула несколько преобразовывается. В ней числитель и знаменатель делятся на f2
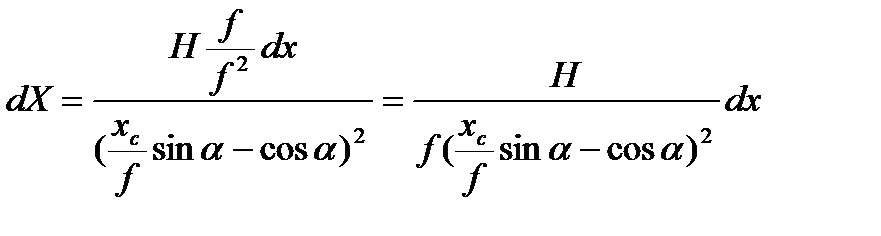
Вводится обозначение 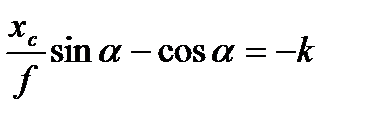 и тогда
и тогда
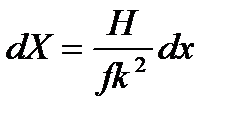 .
.
Для вычисления dY запишем
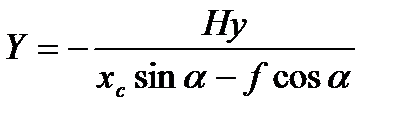 .
.
Тогда
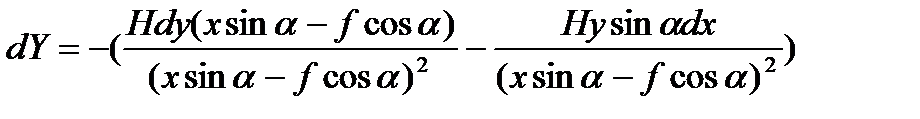
В данной формуле с помощью выражения
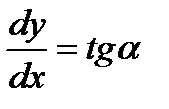
заменим dy через dx и запишем
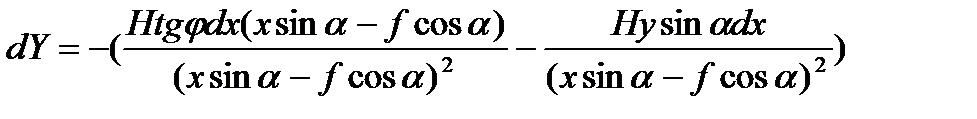
Числители этого выражения разделим и умножим на f, а знаменатели разделим и умножим на f². Тогда
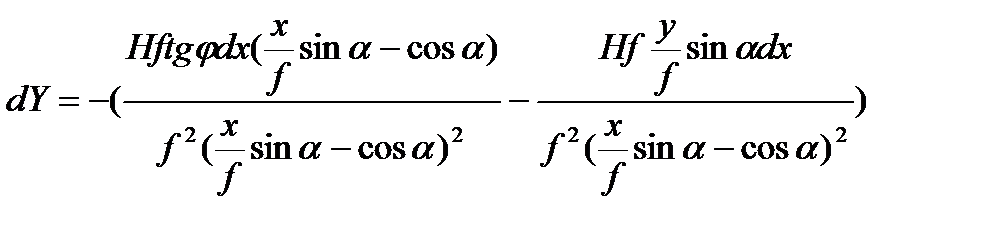 .
.
Обозначая
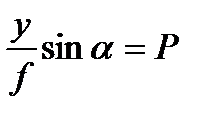
запишем
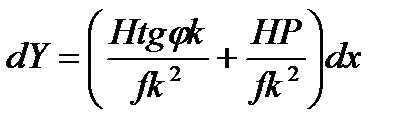
или
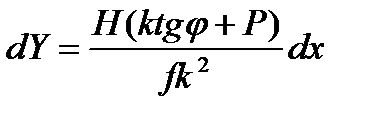
Зная dx , dy, найдем
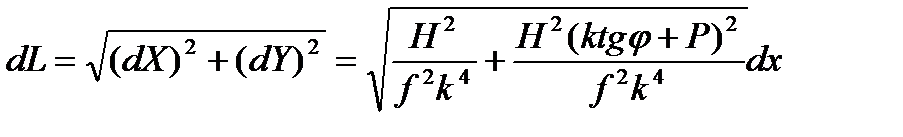
или
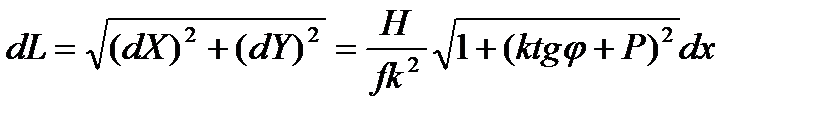 .
.
Вернемся к формуле масштаба
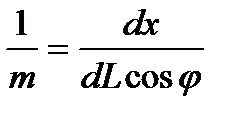
С учетом полученного выражения для dL запишем ее так
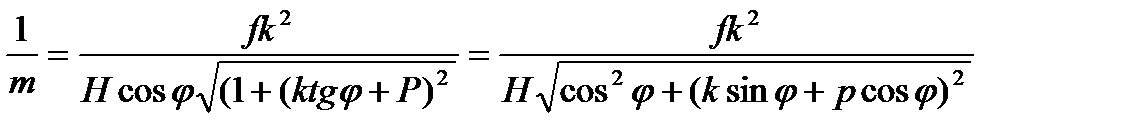 (3.26)
(3.26)
В зависимости от значений φ и угла наклона α возможны различные значения масштаба снимка. Так при φ=0, y=0 в частности будет:
1) в главной точке снимка при x=0 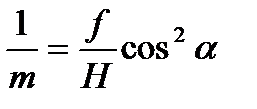 ;
;
2) в точке стояния (n) при х =- ftgα 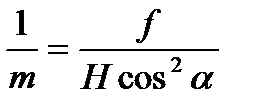 ;
;
3) в точке i при х=fctgα 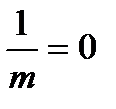 ;
;
4) в точке нулевых искажений c при х=- ftg(α/2) будет k=-1 и 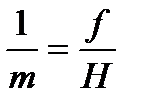
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|