Хелпикс

Главная

Контакты

Случайная статья



Искажение направления из-за рельефа местности

⇐ ПредыдущаяСтр 31 из 56Следующая ⇒


3.6.2. Искажение направления из-за рельефа местности

         Искажение  направления из-за рельефа является следствием смещения точки за рельеф. Поэтому вывод формулы искажения направления  из-за рельефа осуществим на основе чертежа (рис.3.13), который строится на основе рис.3.12.  Из рис.3.13 следует, что

искажение направления из-за рельефа Δφh является функцией смещения точки за рельеф

δh. Для его определения запишем теорему синусов

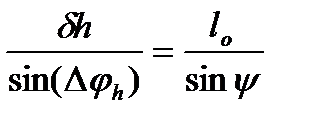
Полагая, что

lo=l,

и заменяя из-за малости значение синуса угла значением самого угла,

запишем

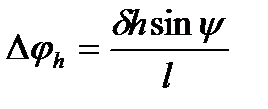.                        (3. 55)

В максимальном случае при

sinψ=1

c учетом (3.53) окончательно имеем в радианах

 

                                                    

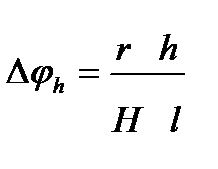
          Для вычисления Δφh в градусах, минутах или секундах необходимо умножить (3.55) на значение радиана в соответствующей угловой мере.

           Пример. Пусть  r=75мм, h =6м, H=1000м, l= 120мм.

Тогда в максимальном случае.

 

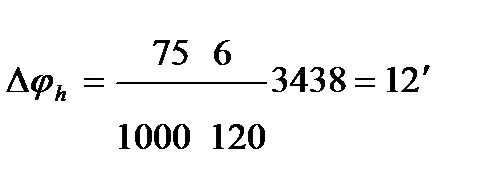                       (3.56)

 

r
a‘
a
ψ
b
Δφh
o
l
δh

 

Рис.3.13. Искажение направления из-за рельефа

Отметим, что при ψ=0 искажения за рельеф также равны нулю. Это значит, что направления, проведенные с главной точки планового снимка не искажаются.

            

3.6.3. Искажение площадей из-за рельефа

В качестве модели для определения названных искажений рассмотрим прямоугольник (рис.3.14), расположенный вдоль оси иксов. Считаем, что настоящий прямоугольник имеет положительный угол наклона  ν (рис.3.15), из-за чего он на рис.3.14 изображается в виде слабо выраженной трапеции.

Искажение площади из-за рельефа будем находить по формуле

Δph=p-po,                                                            (3.57)

где р- площадь, вычисленная по измерениям на аэрофотоснимке, а ро - значение проекции площади на горизонтальную плоскость в масштабе снимка. Поскольку крайние точки прямоугольника симметричны по высоте (+h =-h) относительно плоскости  основания, а линия ef находится на этой плоскости, то значение р можно определить как следующее произведение

р=аb۰ef,                                                               (3. 58).

При этом

ef = ,                                                                 (3.59)

где L‘o- длина горизонтальной проекции поперечной стороны прямоугольника, т. е. длина отрезка ef на местности, f/H - масштаб снимка. Отрезок ab найдем из рисунка (3.15). Для этого запишем

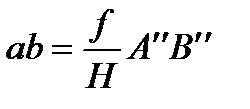.                                                          (3.60)

А‘‘В‘‘ выразим через горизонтальную проекцию Lo , отрезки А‘А‘‘, ‘‘‘

А‘‘В‘‘=Lo+ А‘А‘‘+‘‘‘.

А в соответствии с (3.52) запишем

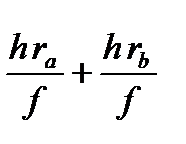А‘‘В‘‘=Lo+ = Lo+ 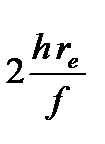    .         (3. 61)

        Учитывая, что исходя из рис. 3.15

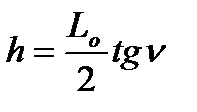
после подстановки (3.61) в (3.60) найдем

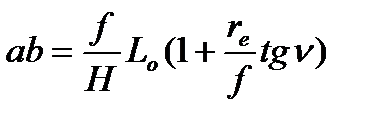                                       (3.62)
Подставляя (3.62) и (3.59) в (3. 58) на основании (3.57) получим

 

.

 

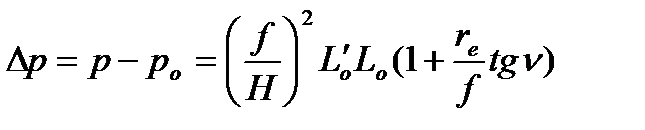Но поскольку

,

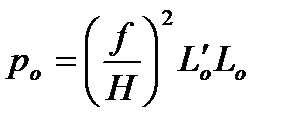то

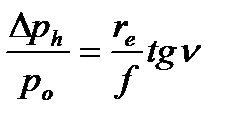                                                    (3.63)

Принимая в соответствии с рис.3.14

где ψр - угол между направлениями из центра снимка на точки е и g –центр фигуры,

 

окончательно получим

 

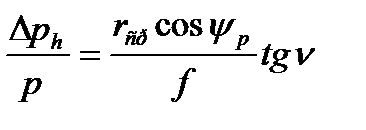                                                                                (3.64)

Здесь для удобства индекс при переменной р специально опущен.

         Пример. Пусть rср=75мм, f=200мм, ν=3°, ψр=0°.

Тогда

                               (3.65)

a
b
c
d
e
f
X
o
ψр
rср
g

Рис.3.14. Изображение прямоугольника  на снимке  из-за влияния рельефа.

 

 

A
S
B
E
+h
-h
a
b
e
A‘‘
ν
f
H
B‘‘
Lo
l
Плоскость основания
A‘
B‘
Рис. 3.15.Влияние рельефа на изображение отрезка местности на снимке

 

 


⇐ Предыдущая26272829303132333435Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.