Монтированием каждого маршрута в отдельности.

Монтированием каждого маршрута в отдельности.

1. Каждый маршрут монтируют на отдельную основу – кальку или тонкую бумагу.

2. Средний маршрут приклеивают к общей основе, оставляя неприклеенными его верхнюю и нижнюю части, т. е. зоны поперечного перекрытия.

3. Следующий (смежный с ним ) маршрут располагают так, чтобы в его середине по поперечному перекрытию достигалось максимальное совпадение контуров. Потом его поворачивают так, чтобы совпадали контура на краях. Или чтобы их поперечные отклонения были одинаковы как по величине, так и по знаку.

4. Поперечным смещением маршрута уменьшают эти отклонения наполовину.

5. Продольным сдвигом маршрута добиваются различных по знаку и одинаковых продольных отклонений.

6. Маршрут подклеивают к основе в средней части и разрезают оба маршрута по поперечному перекрытию. После чего приклеивают крайние части к основе.

Контроль фотосхемы, определение ее масштаба, оформление фотосхемы осуществляется описанным выше способом. Оценка точности при этом осуществляется как по продольным порезам, так и по поперечным

Задача 2.1. Изготовить одномаршрутную и многомаршрутную фотосхемы

3.Анализ одиночного снимка

3.1.Зависимость координат точек местности от координат точек снимка

Исходя из рис.3.1 установим зависимость координат точки местности от координат этой же точки, измеренной на снимке .

Исходной примем фотограмметрическую систему координат XYZ.

Рис. 3.1. Связь координат точек снимка и местности

Вектор 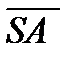обозначим через R_SA_,т.е. 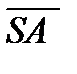= R_SA. А вектор 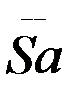через r, т. е.

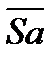= r.

Введем векторы R_А и R_S. А вектор R_SA запишем дважды в следующем виде

R_SA=mr, где m – масштабный фактор и

R_SA= R_А - R_S; (3.1)

Очевидно, что

R_А - R_S= mr (3.2)

Это есть уравнение коллинеарности векторов. Оно является фундаментальным для установления связей между координатами точек снимка и местности.

Перепишем (3.2) в координатном виде:

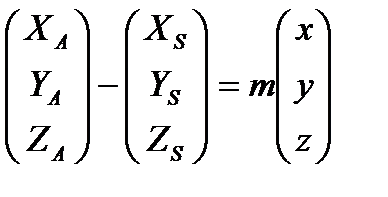; (3.3)

Очевидно, что

X_A-X_S=mx;

Y_A-Y_S=my;

Z_A-Z_S=mz;

Тогда,

X_A=X_S+mx; (3.4)

Y_A=Y_S+my;

Неизвестный множитель m найдем так:

;

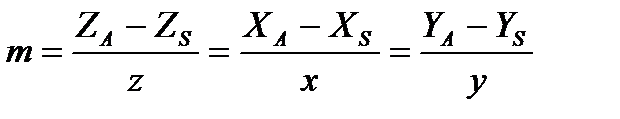Тогда формулы (3.4) примут вид

(3.5)

(3.6)

Настоящие формулы являются основными для установления зависимости координат точек местности от координат точек снимка.

Только выразим в них координаты x,y через измеренные на снимке и элементы внутреннего и внешнего ориентирования снимка.

Координаты точек снимка x, y, z даны в фотограмметрической системе координат, начало которой перенесено в точку фотографирования S. А снимок находится под наклоном к данной системе координат на углы α, ω, æ.(рис.3.2)

Рис.3.2.Первая система внешнего ориентирования снимка

В системе координат снимка координаты точки определяются следующими значениями x_c, y_c, z_c=-f. Задача заключается в том, чтобы от координат x_c, y_c, z_c=-f перейти к координатам x, y, z используя углы наклона снимка α, ω, æ,, называемые еще углами Эйлера. Такой переход осуществляется по формуле

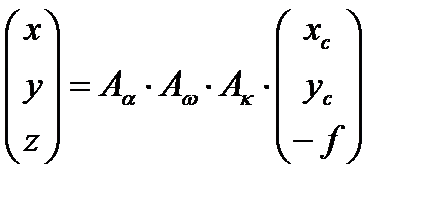, (3.7)

где 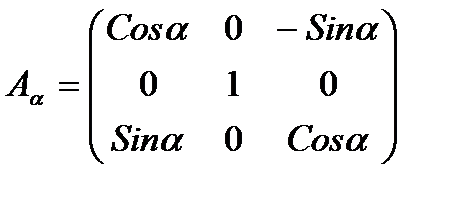, (3.8)

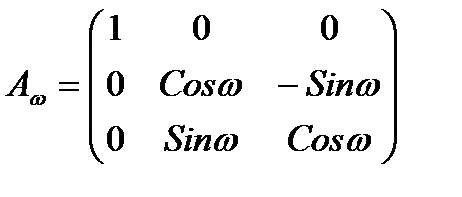, (3.9)

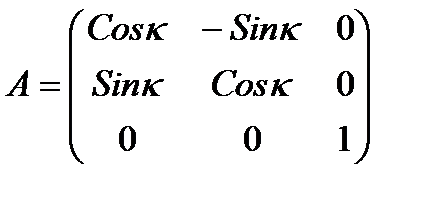. (3.10)

Отметим, что матрица

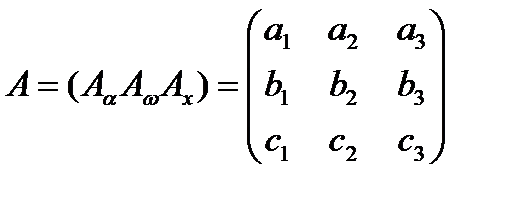
(3.11)

называется матрицей направляющих косинусов.

Таким образом, вычисляя по формуле (3.6) координаты x,y,z и подставляя их в (3.5),(3.6)

находят координаты точки местности в фотограмметрической системе координат.

(3.12)

(3.13)

Пример. Пусть xс=80,637мм, yс=2,517мм, α=3º, ω =0, κ=0. cosα=0,998630, sinα=0,0523360. Значения тригонометрических функций берутся в таких задачах с точностью до шестого знака после запятой и с соблюдением шести значащих чисел.

Тогда

Aα= , Aω=E, Aκ=E, где Е – единичная матрица – матрица с единичными диагональными членами и нулевыми – недиагональными. Тогда А=Аα и в соответствии с (3.6) найдем

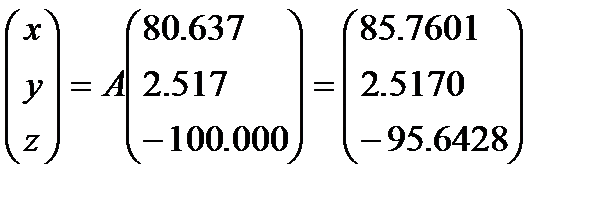
По формулам (3.5),(3.6) окончательно получим

ХА=6426,16+(154,160-1654,17)85,7601/(-95,6428)=7771,176(м),

УА=52346,11+(154,160-1654,17)2,517/(-95,6428)=52385,585(м)

⇐ Предыдущая 19 20 21 22 232425 26 27 28 Следующая ⇒