
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Искажение площади на наклонном снимке плоской местности
3.5.3.Искажение площади на наклонном снимке плоской местности
Влияние угла наклона на искажение площади проиллюстрируем на прямоугольнике, ориентированном вдоль оси х снимка, перспектива которого приведена на рис.3.11.
| y |
| x |
| lx |
| ly |
Рис. 3.11. Перспектива прямоугольника
Искажение площади на наклонном снимке будем анализировать по формуле масштаба(3.26)
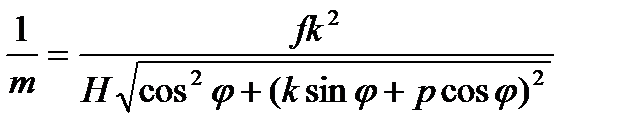
Cтороны прямоугольника на горизонтальном снимке обозначим через lx0, ly0, а на наклонном снимке – через lx, ly .Тогда можно записать

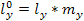
где при φ=0°,Н=f
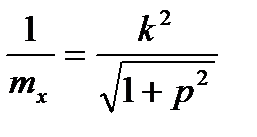 , (3.47)
, (3.47)
а при φ=90°, Н=f
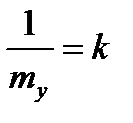 (3.48)
(3.48)
Запишем формулу площади прямоугольника на горизонтальном снимке

Искажение площадей составит
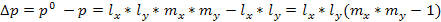 ,
,
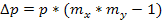 ,
,
 .
.
Теперь в соответствии с (3.47),(3.48) и обозначая Δр через Δрα можно записать
 (3.49)
(3.49)
Пример.Пусть:
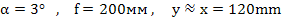
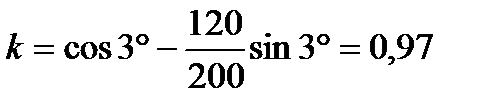 ,
,
 ,
,
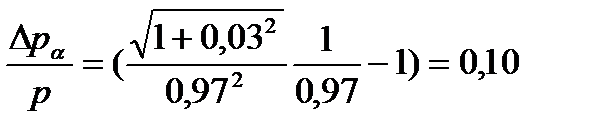 . (3.50)
. (3.50)
Задача 3.5. При заданных x, y, f, φиα в градусах рассчитать:
- смещение точки за наклон снимка по формуле (3.36),
- величину искажения направления по формуле (3.45),
- величину относительного искажения площади по формуле (3.49)
Исходные данные по вариантам приведены в табл. 3.2
3.6. Смещение точек, искажение направлений и площадей на снимке, вызванные рельефом местности
3.6.1 Смещение точек за рельеф
| A‘ |
| H |
| A |
| h |
| A‘‘ |
| f |
| a |
| a‘ |
| r |
| S |
| δh |
| Плоскость основания |
Рис.3.12.Смещение точки за рельеф
При построении планов точки местности отображаются в виде их ортогональных проекций. Так, на рис. 3.12 ортогональной проекцией точки А будет точка А‘ на плоскости основа. Для того, чтобы на снимке также получить ортогональную проекцию точки, необходимо точку а снимка сместить в точку а‘. Такое преобразование изображений точек из центральной проекции в ортогональную называется также трансфрормированием. Найдем величину смещения δh точки а в точку а‘. Для этого запишем пропорцию
 ,
,
из которой следует
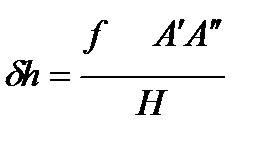 (3.51)
(3.51)
Для исключения А‘А‘‘ запишем пропорцию
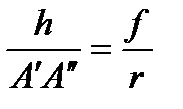 ,
,
из которой следует
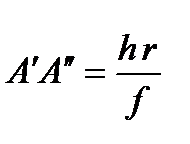 (3.52)
(3.52)
После подстановки (3.52) в (3.51) окончательно получим
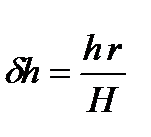 (3.53)
(3.53)
Пример . Пусть r=75мм, h =6м, H=1000м.
Тогда
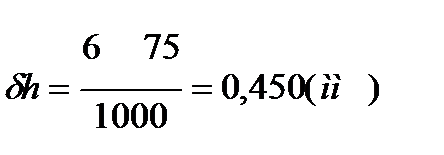 (3.54)
(3.54)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|