Изосова Л.А., Изосов А.В.

Элементы комбинаторики и теории вероятностей. Учеб. пособие. - Магнитогорск: МГТУ, 2008. – 112 с.

Изложены основные понятия комбинаторики, необходимые в курсе теории вероятностей. Основной материал по случайным событиям и случайным величинам приведён с достаточными обоснованиями и снабжён большим количеством примеров в соответствии с программой курса математики.

ЭЛЕМЕНТЫ КОМБИНАТОРИКИ.

Комбинаторный анализ занимается изучением объектов не – которого конечного множества 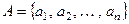и их свойств. Этими объектами могут быть подмножества множес -тва 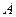, подмножества из множества с повторяющимися элементами, упорядоченные подмножества множества и т.п.

Комбинаторный анализ является разделом дискретной ма -тематики, истоки которой уходят в глубокую древность. В на- стоящее время интерес к нему значительно усилился. Бла – годаря этому, комбинаторный анализ превратился в достаточ- но развитую ветвь математики, которая непрерывно разраста- ется. Это затрудняет задачу очертить круг объектов и их свойств, которые принадлежат этому разделу. Но нас инте- ресуют более прозаические вопросы, а именно те вопросы, которые имеют непосредственное отношение к теории веро -ятностей, т.е. связанные с вычислением количеств появлений тех или иных событий в сериях некоторых испытаний.

При выборе элементов из различных элементов принято говорить, что они образуют соединение из эле –ментов по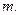

В зависимости от того, имеет ли значение порядок эле -ментов в соединении или нет, а также от того, входят в со- единение все элементов или только часть их, различают три вида соединений.

ВИДЫ СОЕДИНЕНИЙ:

1. Соединения, отличающиеся друг от друга составом эле -ментов или их порядком, каждое из которых содержит 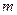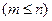элементов, взятых из различных элементов, назы- вается размещением из элементов по

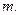
Например, напишем все размещения из элементов 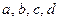по два:

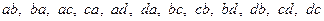2. Соединения, каждое из которых содержит различных

элементов, взятых в определённом порядке, называются пере- становками из элементов.

Например, напишем все перестановки из элементов :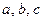

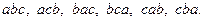
3. Соединения, отличающиеся друг от друга по крайней ме- ре одним элементом, каждое из которых содержит 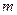элемен- тов, взятых из различных элементов, называются сочета – ниями (комбинациями или выборками) из элементов по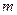

Например, напишем все сочетания из элементов 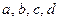по три элемента:

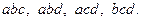
Задача о числе размещений. Сколькими способами можно выбрать и разместить по 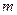различным местам 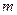из раз- ных предметов (объектов) ? Количество всех таких способов принято обозначать 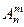(число размещений из по ).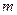

Ясно, что на одно место можно поместить любой из предметов; таким образом:

( ).

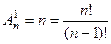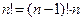Если одно место занято некоторым предметом, то на дру- гое место можно поместить любой из 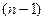оставшихся, по- этому:

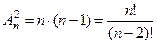Продолжая аналогичные рассуждения, окончательно получим:

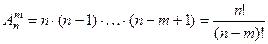Рассмотрим несколько примеров.

Пример 1. Упростить выражение:

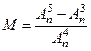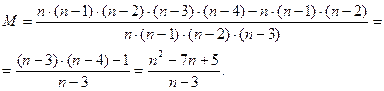
Пример 2. Пусть на плоскости заданы 8 точек. Сколько различных векторов можно построить по этим точкам.

Вектор соединяет две точки, причём важно, какая точка начальная, а какая конечная. Поэтому задача сводится к вычислению числу размещений 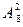. Применяем соответст -вующую формулу:

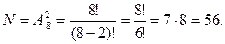
Пример 3. Сколько различных трёхзначных чисел можно составить из цифр: 0, 1, 4, 6, 7, 9.

Число различных размещений из 6 элементов по 3 равно:

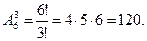
Однако цифра 0 на первом месте не является значимой, поэ- тому из общего числа размещений нужно удалить комбинации, в которых 0 стоит на первом месте, т.е.

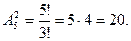
Окончательно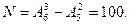

Пример 4. В соревновании по баскетболу университета при- нимают участие 7 команд, представляющих разные факульте - ты. Сколькими способами могут быть распределены призовые места (1 – е, 2 – е и 3 – е) между этими командами ?

В этой задаче опять важен порядок, поэтому опять приме -няем формулу:

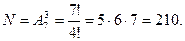
Задача о числе перестановок. Сколькими способами можно переставить различных элементов, расположенных на различных местах? Количество таких перестановок обозна -чается .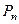

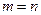Эта задача сводится к нахождению числа размещений элементов на мест, т.е. случай . Учитывая, что, по определению, 0!=1, получаем:

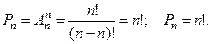
Пример 5. Сколькими способами можно расставить на пол- ке 6 книг различных авторов ?

Пример 6. Русть 7 занумерованных шариков произвольным образом бросают в решётку с 7 – ю ячейками. Сколькими спо -собами шарики могут распределиться по ячейкам, при условии,

что каждый шарик попадает в какую – то одну ячейку.

Задача сводится к вычислению числа перестановок:

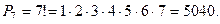
Задача о числе сочетаний. Сколькими способами можно вы- брать 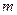из различных предметов. Количество всех таких способов принято обозначать 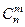(число сочетаний из по 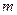, без учёта порядка элементов).

Выбрать 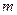из различных предметов можно 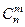спосо-бами, а возможностей упорядочить предметов из данного соче- тания - 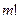. Поэтому имеется 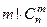возможностей выбрать и разместить по 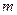разным местам 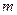из разных предметов, т.е. 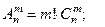тогда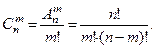

Легко доказать следующие свойства числа сочетаний:

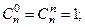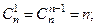1. 2. 3.

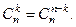
Приведём несколько прмеров применения формулы числа сочетаний из по 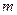элементов

Пример 7. 12 человек играют в городки. Сколькими спо -собами они могут выбрать команду из 4 человек на сорев –нование ?

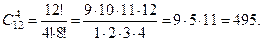
Пример 8. В выпуклом семиугольнике проведены всевоз -можные диагонали, причём никакие три из них не пересека- ются в одной точке (т.е. не выходят из одной вершины). Сколько точек пересечения имеют данные диагонали ?

Каждой точке пересечения диагоналей в этом случае соот – ветствует 4 вершины семиугольника, а каждой четвёрке вер -шин соответствует одна точка пересечения диагоналей. Поэто- му число точек пересечения диагоналей семиугольника равно числу способов выбрать четыре вершины из семи, т.е.

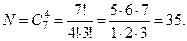
Пример 9. В розыгрыше первенства по футболу участвует 16 команд, причём любые две команды играют между собой только один раз. Сколько всего произведено игр ?

Поставленная задача - задача о числе выборок из 16 по 2. Поэтому:

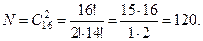
Пример 10. Из 2 математиков и 10 экономистов необходимо составить комиссию в составе 8 человек. Сколькими способа -ми может быть составлена комиссия, если в неё должен вхо -дить хотя бы один математик ?

Самый простой способ найти количество способов составле- ния таких комиссий - это от общего числа вариантов комис -сий, составленных из 12 человек по 8, отнять количество ко -миссий, в которых нет ни одного математика, т.е.

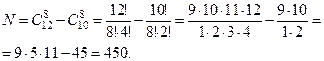
Пример 11. Из большого букета, содержащего 12 роз, 9 хризантем, 15 гвоздик и 7 герберов случайным образом наби- рают букет из 15 цветов. Сколькими способоми можно набрать

такой букет, чтобы в нём было 3 розы, 5 хризантем, 5 гвоз -дик и 2 гербера.

Общее количество цветов в набираемом букете - 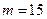, причём,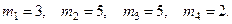

Общее количество всех цветов - 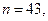причём,

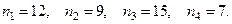
Тогда число вариантов находится следующим образом:

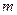До сих пор мы рассматривали соединения, в каждое из ко- торых любой из различных элементов входит один раз. По- мимо этого можно рассматривать соединения, в которые лю -бой из элементов может входить более одного раза, т.е. соединения с повторениями. В задачах с повторениями не имеет значения, что больше или .

Задача о числе размещений с повторениями. Сколькими способами можно разместить на 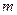мест 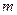элементов, для каждого из которых есть различных вариантов ? Количество таких размещений обозначается 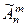и равно:

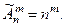
Пример 12. Пусть каждый телефонный номер состоит из 6 цифр. Сколько существует телефонных номенов, содержащих только цифры: 2, 4, 6, 8 .

В этом примере 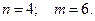Тогда

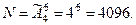
Пример 13. В секретном замке на общей оси находятся че- тыре диска, каждый из которых разделён на 5 секторов, на ко- торых записаны цифры от 0 до 4. Сколько возможно различ -ных кодовых вариантов ?

Здесь 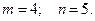Тогда

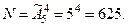
Пример 14. Сколькими способами можно разместить 7 пасса- жиров в 3 вагона ?

В данном случае, 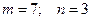и, следовательно,

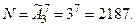
Задача о числе перестановок с повторениями. Сколькими способами можно переставить различных предметов 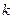раз- ных типов, количества каждого из которых равны, соответст -венно 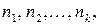( причём ) ?

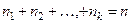Если учесть, что при перестановке элементов оного типа ничего не изменяется, т.е. получаем выражения того же вида, то перестановок с повторениями будет меньше, чем обычных перестановок, а именно, для определения количества таких пе- рестановок необходимо общее число перестановок разделить на число перестановок среди одинаковых элементов, т.е.

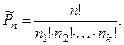
Пример 15. Сколько различных перестановок можно выпол -нить в слове «фантастика» ?

Здесь 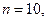ф - 1 ( 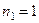), а - 3 ( 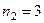), н, с, и, к - 1 ( 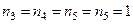), т - 2 ( 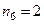). Тогда

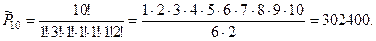
Пример 16. Сколькими способами можно упаковать девять различных книг в трёх бандеролях соответственно по две, три и четыре книги в каждой бандероли?

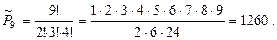
Пример 17. Сколькими способами можно распределить де -сять молодых специалистов по трём цехам комбината в кото- рых требуется 5, 3 и 2 специалиста, соответственно ?

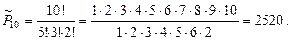
Сочетаниями из предметов по 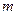с повторениями на -зываются соединения, содержащие 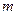предметов (без учёта порядка следования), причём каждый предмет может входить в соединение некоторое число раз, не больше .

Задача о числе сочетаний с повторениями. Если имеется по 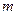одинаковых предметов каждого из различных типов, то сколькими способами можно выбрать 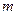из этих 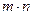предметов?

Число таких сочетаний с повторениями обозначается и вычисляется по формуле:

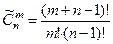Рассмотрим несколько прмеров:

Пример 18. В кондитерской имеется 10 сортов пирожных. Сколькими способами можно купить 4 пирожных?

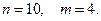Тогда

Пример 19. В почтовом отделении имеется в наличии 5 видов открыток «С праздником 8 Марта». Сколькими спосо- бами можно купить 10 поздравительных открыток ?

В этом примере 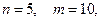тогда:

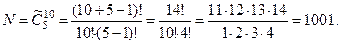
Пример 20. Сколькими способами можно выбрать 5 монет из 5 - ти двух рублёвых монет и 5 - ти одно рублёвых монет?

Это задача о сочетаниях из двух по пяти с повторениями.

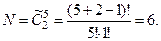
Замечание. Как и для случая размещений с повторениями, при вычислении числа сочетаний с повторениями, не имеет значения, что больше 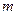или .

Итак, мы рассмотрели основные комбинаторные задачи, которые необходимы нам при вычислении вероятностей событий.

ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

СЛУЧАЙНЫЕ СОБЫТИЯ

§ 1 ПРЕДМЕТ ТЕОРИИ ВЕРОЯТНОСТЕЙ.

Одним из основных понятий, которыми оперирует теория

вероятностей, является событие.

Событием в теории вероятностей называется любой резуль- тат, который может произойти в итоге некоторого опыта (испы- тания).

Все наблюдаемые нами события могут быть подразделены на три вида: достоверные, невозможные и случайные.

Достоверными называют события, которые обязательно про- изойдут при выполнении определённой совокупности условий.

Например, достоверным является событие: «при бросании игрального кубика выпала цифра не больше 6».

Невозможным называется событие, которое заведомо не произойдёт при выполнении определённых условий.

Например, невозможным является событие: «при бросании игрального кубика выпала цифра 8».

Случайным (или возможным) называется событие, которое может произойти или не произойти в данных условиях.

Например, в том же опыте, случайным является событие: «при бросании игральньго кубика выпала цифра 3».

Каждое случайное событие зависит от действия многих слу- чайных причин, причём невозможно учесть влияние этих причин на результат (их много и законы их действия непредсказуе -мы). Поэтому теория вероятностей не ставит перед собой за- дачу предсказать наперёд, произойдёт ли данное конкретное событие или нет. Но, если рассматриваются случайные собы- тия, которые могут многократно наблюдаться в одних и тех же условиях (например, многократное подбрасывание монеты), т.е., если речь идёт о массовых однородных событиях, то оказы -вается такие однородные события, независимо от их конкрет- ной природы, подчинены определённым закономерностям, а именно вероятностным закономерностям.

Итак, предметом теории вероятностей является изу -чениевероятностных закономерностей массовых одно -родных случайных событий.

Знание закономерностей, которым подчинены массовые од- нородные случайные события позволяет предвидеть, как эти события будут проистекать. Можно, например, предсказать с небольшой погрешностью число появлений «герба», если моне- та будет подброшена большое число раз.

Методы теории вероятностей широко применяются в раз -личных отраслях науки и техники (теоретическая физика, тео- рия надёжности, теория стрельбы, теория ошибок наблюдений, общая теория связи, геодезия, астрономия и т.д.)

Теория вероятностей служит также базой математической и прикладной статистики, которые, в свою очередь, используются при планировании и организации производства, при анализе технологических процессов, при контроле качества производст -ва и т.п.

Первые работы, в которых зарождались основные понятия теории вероятностей, представляли собой попытки создания теории азартных игр (Кардано, Гюйгенс, Паскаль, Ферма и др. в 16 -17 веке). Следующий этап развития теории вероятностей связан с именем Бернулли (1654 – 1705) Доказанная им теоре- ма «Закон больших чисел» была первым теоретическим обос- нованием накопленных ранее фактов. Дальнейшим успехам те- ория вероятностей обязана Муавру, Лапласу, Гауссу, Пуассону и др. Наиболее плодотворный период развития теории вероят- ностей связан с известными именами русских математиков, та- ких как Чебышев, Ляпунов, Марков (19 – 20 век). В этот пери -од теория вероятностей становится строгой математической на- укой.

§ 2 ПРОСТРАНСТВО ЭЛЕМЕНТАРНЫХ СОБЫТИЙ,

АЛГЕБРА СОБЫТИЙ.

Будем различать элементарные (неразложимые) события и составные события (или просто события).

Пример 1: подбрасывание игральной кости 1 раз. Элемен -тарные события, обозначим их 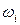, число выпавших очков на верхней грани ( 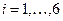), Множество всех элементарных событий в данном опыте 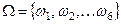. Составные события, или просто события, могут быть описаны как подмно- жества множества всех элементарных событий. Например, cо- бытие А - «выпало чётное число очков» можно выразить сле- дующим образом .

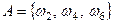Пример 2: Трёхкратное подбрасывание монеты.

Пусть 1 - выпал «герб», 0 – выпала «цифра». Тогда множество всех элементарных событий:

     .

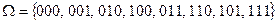Событие А - «при первом подбрасывании выпал герб» можно представить следующим образом»:

               .

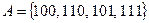Пример 3. Стрельба по плоскости.

Если мы введём на плоскости прямоугольную систему коор -динат 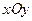, то множнство элементарных событий (попадание в некоторую точку плоскости) записывается в виде:

     .

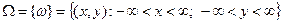Событие А - «попадание в круг единичного радиуса» можем записать в виде .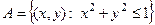

Итак, элементарные события - это все мыслимые исходы опыта или наблюдения. События могут быть описаны как под- множества множества всех элементарных событий. Совокуп -ность всех элементарных событий данного опыта будем назы- вать пространством элементарных событий и обозначать 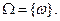  Оно может быть конечным, как в приерах 1 и 2, счётным ( 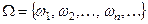) или бесконечным несчёт- ным, как в примере 3. Любое подмножество иножества  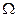 называется событием.

Суммой (или объединением) двух событий 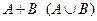  называется событие, состоящее из элементарных событий, вхо- дящих по крайней мере в одно из событий А или В.

Например: 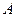= «попадание в цель при 1 - м выстреле»,  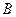 - «попадание в цель при 2 – м выстреле», тогда 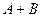- «хотя бы одно попадание в цель».

Следует помнить свойство: .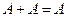

Произведением (или пересечением ) 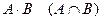двух событий называется событие, состоящее из элементарных со- бытий, входящих и в событие  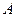 и в событие .

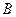Например: 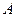= «попадание в цель при 1 - м выстреле»,  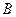 - «попадание в цель при 2 – м выстреле», тогда 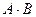- попа- дание в цель при обоих выстрелах.

Свойство: .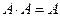

Разностью 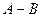( или 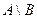) называется событие, состо- ящее из элементарных событий, входящих в множество 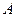, но не входящих в множество 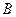. ( Другими словами, событие  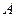   произошло, а событие  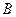 не произошло.)

Например, при бросании игрального кубика: 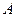  - «выпала чётная цыфра», т.е. 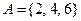,  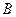 - «выпала цыфра, крат- ная 3», т.е. 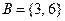. Тогда .

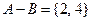Событие 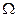, состоящее из всех элементарных исходов данного опыта, называется достоверным событием (проис- ходит «всегда» в данном опыте).

Событие 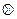, не содержащее ни одного из элементарных исходов данного опыта, называется невозможным событием.

Например, при бросании игрального кубика «выпала цифра от 1 до 6» - достоверное событие, «выпала цифра 10» - не -возможное собтие.

Противоположное событие 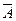  (событие  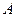 не произошло) - это дополнение события  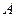 до достоверного, т.е. .

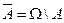Например: 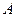  - «три дня подряд шёл дождь», тогда 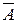- «хотя бы один день дождя не было»;  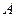 - «из пяти чисел хо -тя бы одно чётное», тогда  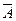 - «все пять чисел нечётные».

Свойства: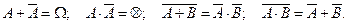



События 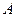  и 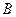  называются несовместными, если невоз -можно их одновременное появление в одном опыте, (т.е., если ).

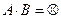Например, при бросании монеты: 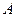  - «выпал герб»,  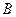 - «выпала цифра» - несовместные события.

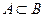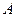  ( влечёт 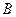, т.е элементарные события, входя -щие в событие 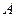, входят и в событие 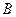) - из наступления события  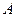 следует наступление события .

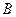Например: 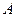  - «попадание при первом выстреле», 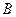- «хотя бы одно попадание при трёх выстрелах». Тогда .

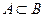Есл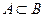и   и 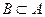, то говорят, что события  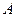 и 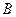  равносильны или эквивалентны.

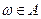  означает, что элементарное событие  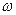 входит в событие .

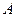Понятия произведения и суммы событий можно перенести на случай произвольной конечной или бесконечной последо -вательности событий:

Событие 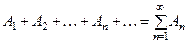состоит из элемен -тарных событий, входящих хотя бы в одно из событий , .

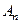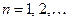Событие 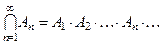  состоит из элементарных событий, входящих одновременно в каждое из событий , .

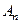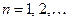Говорят, события 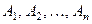  образуют полную группу, если в результате опыта происходит хотя бы одно из них.

Пусть 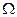  - произвольное пространство элементарных собы- тий. 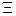- некоторый класс подмножеств пространства 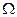. Этот класс подмножеств называется алгеброй событий, если  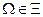 и для любых событий  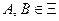 выполняется: , .

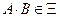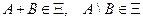§ 3 ЧАСТОТА СОБЫТИЯ И ЕЁ СВОЙСТВА,

Пусть произведена серия 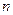  испытаний, в каждом из кото -рых может появиться или не появиться событие .

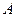Частотой события 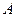  в данной серии испытаний называ –ется отношение числа 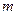испытаний, в которых появилось со- бытие 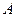, к общему числу 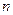испытаний, т.е. .

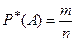       СВОЙСТВА ЧАСТОТЫ СОБЫТИЯ.

1) Частота случайного события 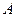  неотрицательное число, не большее единицы, т.е.

                             .

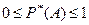Это свойство очевидно, так как всегда .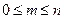

2) Частота достоверного события равна единице 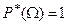  (так как ).

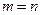3) Частота невозможного события равна нулю . (так как в этом случае ).

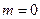4) Частота суммы двух несовместных событий равна сум- ме частот этих событий, т.е.

                .

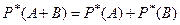В самом деле, если событие 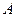  появилось  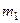 раз, а со- бытие  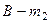 раз в 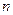  испытаниях, то, так как события не –совместны и невозможно их одновременное появление в дан- ных испытаниях, событие  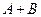 появится  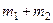 раз.

Тогда

.

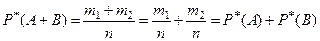Чтобы сформулировать следующее свойство, введём ещё одно понятие. Частота одного события, вычисленная при ус- ловии, что произошло другое событие, называется условной частотой и обозначается 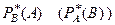. Если события  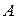 и 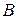  совместны, то можем сформулировать свойство ум- ножения частот.

5) Частота произведения двух событий равна произведе –

нию частоты одного из них на условную частоту другого

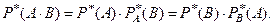                            (1)

В самом деле, пусть в серии из 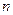  испытаний событие  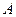 появилось  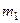 раз, событие 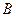-  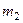 раз, а вместе эти собы- тия появились 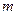раз. Тогда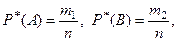

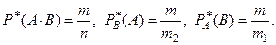Если мы подставим все эти частоты в формулу (1), то получим тождество :

                           .

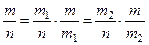Длительные наблюдения показали, что если в одинаковых условиях производятся опыты, в каждом из которых число ис -пытаний достаточно большое, то частота события проявляет свойство устойчивости: в различных опытах частота меня- ется мало (тем меньше, чем больше число испытаний в опыте) и колеблется относительно некоторого постоянного числа.

§ 4 ВЕРОЯТНОСТЬ СОБЫТИЯ.

Учитывая свойство устойчивости частоты события, можно ввести понятие вероятности события.

Определение. Вероятностью случайного события назы –вается постоянное число, около которого группируются часто- ты этого события по мере увеличения числа испытаний.

Это определение вероятности называется статистическим.

Положительное свойство этого определения заключается в том, что оно опирается на реальный эксперимент. Но в этом же кроется и его отрицательная сторона. Для надёжного опреде -ления вероятности, в смысле этого определения, необходимо произвести большое число опытов, что зачастую связано с большими материальными затратами, например, при проверке изделий на надёжность, которая приводит к разрушению изде- лия. Однако то, что каждое массовое случайное событие имеет свою вероятность, является фактом, подтверждаемым опытом, что и доказывает существование статистических закономернос- тей в природе.

Однако статистическое определение вероятности, как осно- ванное на экспериментальных данных, не даёт возможности заранее, до эксперимента, определить вероятность события, т.е. не является «рабочим определением».

Рассмотрим другое определение вероятности, которое на -зывается классическим. Это определение основано на понятии равновозможных несовместных событий (исходов данного опы -та, которые образуют полную группу, т.е. учтены все возмож -ные исходы данного опыта), т.е. шансов. Рассмотрение таких групп равновозможных событий можно свести к так называе -мой «схеме урн» (урна содержит одинаковые, неразличимые на ощупь шарики: разноцветные или занумерованные, которые из- влекаются произвольным образом). Например, испытание с подбрасыванием монеты можно сравнить с извлечением из ур- ны, содержащей два шара (белого и чёрного), шара опреде -лённого цвета. Опыт «подбрасывание игрального кубика» рав- носилен опыту «извлечение из урны, содержащей 6 занумеро- ванных шаров, шара с определённым номером» и т.п.

По отношению к каждому событию равновозможные исходы (шансы) делятся на благоприятные, при которых событие про- исходит, и, соответственно - неблагоприятные, при которых со- бытие не происходит. Например, при бросании игрального ку –бика, для события 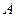  - «выпало чётное число» благоприятны- ми являются 3 шанса - выпали цыфры 2, 4, 6.

Определение. Вероятностью   появления некоторого собы- тия называется отношение числа шансов, благоприятствующих данному событию, к общему числу равновозможных в данном опыте шансов. Такое определение вероятности называется классическим.

Другими словами 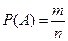, где 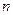  - общее число равно- возможных исходов, а 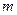- число благоприятных исходов.

Важным достоинством этого определения является то, что с его помощью вероятность события можно определить зара- нее, до опыта, и сделать соответствующие выводы.

Недостаток его заключается в том, что это определения можно применять только в случае равновозможных исходов опыта.

Рассмотрим несколько примеров.

1. Двоекратное подбрасывание монеты. Возможные исходы

«ГГ, ГЦ, ЦГ, ЦЦ» (Г – герб,

⇐ Предыдущая 1 2 3 4 5 6 7 8 910