
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Изосова Л.А., Изосов А.В. 4 страница
Событие 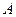 - автомобиль имеет некомплектность. Тогда, по условию,
- автомобиль имеет некомплектность. Тогда, по условию, 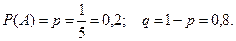
а) По формуле (1),
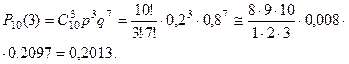
б) Событие 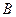 - «хотя бы три автомобиля некомплектны», те. от 3 – х до 10 – ти. Его вероятность проще искать через вероятность противоположного событие
- «хотя бы три автомобиля некомплектны», те. от 3 – х до 10 – ти. Его вероятность проще искать через вероятность противоположного событие 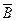 - «менее 3 – х ав- томобилей некомплектны».
- «менее 3 – х ав- томобилей некомплектны».
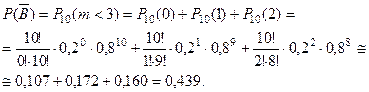 Тогда
Тогда 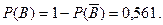
Так как события, состоящие в различном числе появлений события 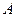 в серии из
в серии из 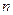 независимых испытаний образуют полную группу несовместных событий, то сумма их вероят -ностей равна единице, т.е.
независимых испытаний образуют полную группу несовместных событий, то сумма их вероят -ностей равна единице, т.е.
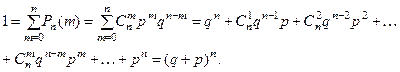
Эта сумма представляет собой разложение 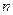 - й степени бинома (бином Ньютона) и связанное с ней распределение вероятностей числа появлений события
- й степени бинома (бином Ньютона) и связанное с ней распределение вероятностей числа появлений события 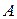 в серии из
в серии из 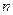 опытов называется биномиальным распределением.
опытов называется биномиальным распределением.
Учмтывая это, для вычисления вероятностей возможного числа появлений события 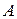 в серии из
в серии из 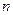 независимых ис- пытаний можно ввести так называемую производящую функ- цию :
независимых ис- пытаний можно ввести так называемую производящую функ- цию :
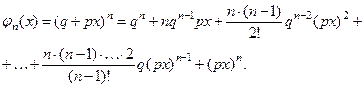
Эта функция обладает тем свойством, что коэффициент, стоя- щий перед 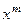 в этой сумме равен вероятности
в этой сумме равен вероятности 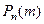 .
.
Пример 2. Предполагается, что в среднем 20% открываю –щихся малых предприятий разоряются в течение года. Найти вероятность того, что после года работы из 6 – ми вновь от - крывшихся предприятий не разорится: а) ровно 5; б) хотя бы четыре.
Вероятность того, что предприятие разорится 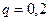 , со - ответственно, вероятность того, что оно не разорится, равна
, со - ответственно, вероятность того, что оно не разорится, равна  Для решения воспользуемся производящей функцией.
Для решения воспользуемся производящей функцией.
 Непосредственным сложением можем проверить, что сумма всех коэффициентов в этом разложении равна 1. Тогда, в случае а):
Непосредственным сложением можем проверить, что сумма всех коэффициентов в этом разложении равна 1. Тогда, в случае а): 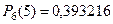 , т.е. коэффициент, стоящий перед
, т.е. коэффициент, стоящий перед  . В случае б):
. В случае б): 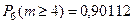 , т.е. сумма коэффициен- тов, стояший перед
, т.е. сумма коэффициен- тов, стояший перед 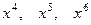 .
.
Аналогичную производящую функцию можно ввести и для случая, когда в серии из 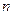 испытания вероятности появления события в каждом испытании различны. Пусть вероятность по- явления события в испытании равна
испытания вероятности появления события в каждом испытании различны. Пусть вероятность по- явления события в испытании равна 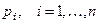 и, соот- ветственно, вероятность того, что событие не произошло -
и, соот- ветственно, вероятность того, что событие не произошло - 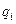 . Тогда о вероятностях определённого числа появлений события
. Тогда о вероятностях определённого числа появлений события 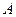 в данной серии опытов можно судить по значению коэф -фициентов перед определёнными степенями
в данной серии опытов можно судить по значению коэф -фициентов перед определёнными степенями 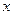 в разложении по степеням
в разложении по степеням 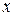 следующей производящей функции:
следующей производящей функции:
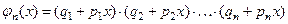 .
.
Пример 3. Пусть пять баскетболистов бросили по одному разу мяч в корзину. Найти вероятность того, что будет три точных попадания, если для 1 – го и 3 – го вероятности попа -дания равны 0,7, для 2 –го - 0,6, для 4 – го - 0,8 и для 5 – го - 0,9.
В этих условиях, 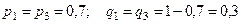 ,
,

Тогда производящая функция имеет вид:
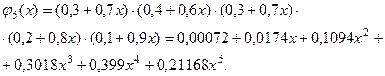 Сумма коэффициентов в разложении равна единице.
Сумма коэффициентов в разложении равна единице.
Тогда вероятность того, что будет три попадания мяча в кор- зину равна коэффициенту перед 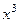 , т.е.
, т.е. 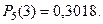
Если бы мы искали эту вероятность, применяя теоремы сло- жения и умножения вероятностей, то вычисления были бы на- много более громоздкими.
Определение. Наивероятнейшим числом 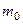 появлений со- бытия
появлений со- бытия 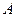 в серии из
в серии из 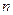 независимых испытаний называется число, для которого
независимых испытаний называется число, для которого 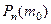 является наибольшим.
является наибольшим.
Например, в примере 2, 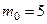 ; в примере 2 ,
; в примере 2 , 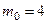 .
.
Используя формулу Бернулли, можно вывести формулу для нахождения наивероятнейшего числа появлений события:
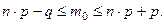 (2)
(2)
Замечание. Длина промежутка, определяемого этими нера- венствами равна единице: 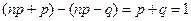 , поэтому, если границы промежутка дробные, то
, поэтому, если границы промежутка дробные, то 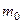 определяется однозначно, если же целые - получаем два значения для
определяется однозначно, если же целые - получаем два значения для 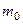 .
.
Пример 4. Вероятность попадания в мишень при каждом выстреле равна 0,7. Найти наивероятнейшее число попаданий в мишень при 8 – ми выстрелах и определить вероятность такого числа попаданий.
В этом примере 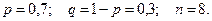 Тогда
Тогда 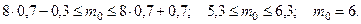
Теперь найдём вероятность:
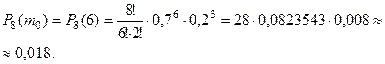
§ 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ В СХЕМЕ БЕРНУЛЛИ.
Если число испытаний достаточно велико, то пользоваться формулой Бернулли не очень удобно. Представьте себе, что требуется вычислить такую вероятность:
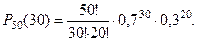
Возникает вопрос, можно ли вычислить такую вероятность, не прибегая к формуле Бернулли. Оказывается можно. Для частного случая 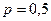 формула для приближённого вы -числения определённого числа появлений события
формула для приближённого вы -числения определённого числа появлений события 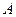 для слу- чая большого числа независимых испытаний была найдена ещё в 1730 году Муавром, а в 1783 году эту формулу обоб -щил Лаплас для произвольного случая
для слу- чая большого числа независимых испытаний была найдена ещё в 1730 году Муавром, а в 1783 году эту формулу обоб -щил Лаплас для произвольного случая 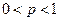 . Поэтому ни- жеследующую теорему иногда называют теоремой Муавра – Лапласа. Доказательство её довольно громоздко, поэтому при- ведём только её формулировку и примеры.
. Поэтому ни- жеследующую теорему иногда называют теоремой Муавра – Лапласа. Доказательство её довольно громоздко, поэтому при- ведём только её формулировку и примеры.
Локальная теорема Лапласа. Если вероятность появления события 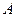 в серии из
в серии из 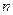 независимых испытаний постоянна и удовлетворяет неравенству
независимых испытаний постоянна и удовлетворяет неравенству 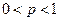 , то вероятность того, что в этой серии испытаний событие появится ровно
, то вероятность того, что в этой серии испытаний событие появится ровно 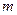 раз приближённо вычисляется по формуле:
раз приближённо вычисляется по формуле:

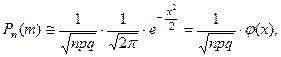 (1)
(1)
где 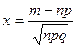 .
.
Во всех справочниках приведены таблицы для вычисления функции 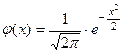 для положительных значений
для положительных значений 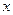 , так как
, так как 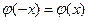 . Но, в принципе, значения этой функ- ции можно вычислить и непосредственно. Точность приближе- ния тем больше, чем больше
. Но, в принципе, значения этой функ- ции можно вычислить и непосредственно. Точность приближе- ния тем больше, чем больше 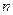 .
.
Пример 1. В среднем 95% часов, поступающих в продажу, не требуют дополнительной регулировки. Найти вероятность того, что из 300 часов, поступивших в продажу, не будет требовать дополнительной регулировки ровно 280.
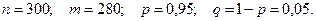
Тогда 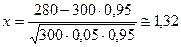 ,
, 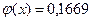 и получаем
и получаем
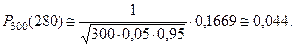
Пример 2. Фирма по установке пластиковых окон расклады- вает рекламные листы по почтовым ящикам. В результате это- го примерно в одном случае из 1000 поступает заказ на изго-товление окна. Найти вероятность того, что при распростране- нии 100000 рекламных листов поступит 90 заказов.
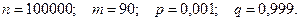
Тогда 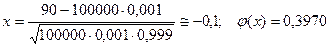 и получаем
и получаем
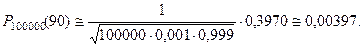
По мере увеличения числа испытаний вероятность того, что некоторое интересуемое нас событие произойдёт определён -ное точное количество раз становится очень близка к нулю, так как число возможных вариантов слишком велико. Поэтому чаще ставится задача определить вероятность того, что число появлений этого события заключено в некотором промежутке. В этом случае работает
Интегральная теорема Лапласа. Если вероятность появле- ния события 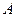 (
( 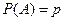 ) в серии из
) в серии из 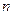 независимых ис –пытаний постоянна, причём
независимых ис –пытаний постоянна, причём 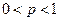 , то вероятность того, что событие появится больше
, то вероятность того, что событие появится больше 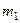 , но меньше
, но меньше 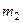 раз приближён- но вычисляется по формуле:
раз приближён- но вычисляется по формуле:
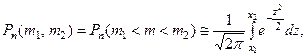 (2)
(2)
где 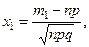
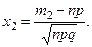
Теорему доказывать не будем, но применяя эту теорему, также можем пользоваться специальной таблицей, тем более, что интеграл  не вычисляется через элементарные функции. В таблицах приведены значения для функции
не вычисляется через элементарные функции. В таблицах приведены значения для функции 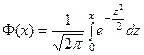 , которую называют функцией Лапласа.
, которую называют функцией Лапласа.
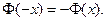 В таблицах приведены значения этой функ- ции для
В таблицах приведены значения этой функ- ции для 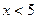 . При
. При 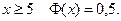
Чтобы можно было пользоваться таблицей, преобразуем формулу (2)
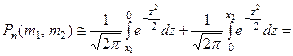
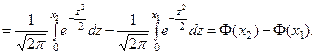
Таким образом, 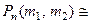
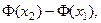 где
где
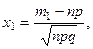
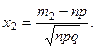
Пример 3. В условиях примера 1, определить вероятность того, что не менее 280 часов не потребуют дополнительной регулировки, т.е. найти вероятность 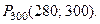
По условию, 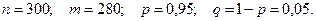
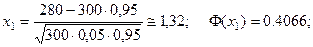
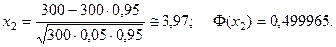
Тогда 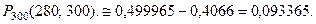
Пример 4. В условиях примера 2, определить вероятность того, что поступит от 80 до 120 заказов на окна.
По условию,
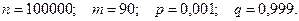
Тогда 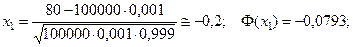
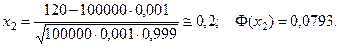
Следовательно, 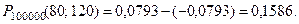
Прямым следствием интегральной теоремы Лапласа являет- ся формула для вычисления вероятности отклонения отно -сительной частоты от постоянной вероятности в незави -симых испытаниях. Пусть произведено 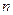 независимых испы -
независимых испы -
таний, в каждом из которых вероятность события 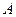 постоян- на и
постоян- на и 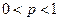 . Тогда вероятность того, что относительная час- тота появления события
. Тогда вероятность того, что относительная час- тота появления события 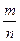 отклонится от вероятности
отклонится от вероятности 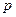 это- го событие по абсолютой величине не больше, чем на
это- го событие по абсолютой величине не больше, чем на 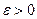 вычисляется по формуле:
вычисляется по формуле:
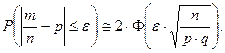 (3)
(3)
Пример 5. Вероятность того, что изготовленная деталь стан- дартна, равна 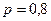 . Найти вероятность того, что среди отобранных 900 деталей относительная частота стандартных деталей, по абсолютной величине, отклонится от вероятности не больше, чем на 0,04.
. Найти вероятность того, что среди отобранных 900 деталей относительная частота стандартных деталей, по абсолютной величине, отклонится от вероятности не больше, чем на 0,04.
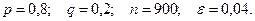 Тогда
Тогда
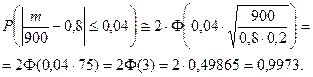
Пример 6. Вероятность появления события в каждом из не -зависимых испытаний равна 0,2. Найти наименьшее число ис- пытаний 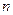 , при которых с вероятностью 0,99 можно ожидать, что относительная частота появлений события отклонится от его вероятности по абсолютной величине не больше чем на 0,03.
, при которых с вероятностью 0,99 можно ожидать, что относительная частота появлений события отклонится от его вероятности по абсолютной величине не больше чем на 0,03.
По условию, 

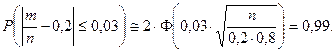
Тогда 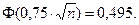
По таблице значений функции Лапласа, видим, что 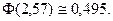 Тогда
Тогда

Пример 7. Отдел технического контроля проверяет 500 из- делий на брак. Вероятность бракованного изделия в проверяя- емой партии равна 0,02. С вероятностью 0,96 определить гра- ницы, в которых будет заключено число 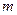 бракованных изде- лий в данной партии.
бракованных изде- лий в данной партии.
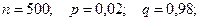
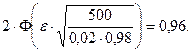 Тогда
Тогда 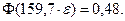
По таблице получаем 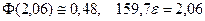 и
и 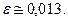 Таким образом, отклонение относительной часто –ты бракованных изделий от постоянной вероятности с вероят -ностью 0,96 удовлетворяет нераверству
Таким образом, отклонение относительной часто –ты бракованных изделий от постоянной вероятности с вероят -ностью 0,96 удовлетворяет нераверству 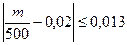 ,
,
или 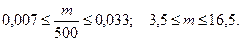 Так как
Так как 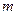 - целое число, то получаем:
- целое число, то получаем: 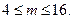
Сдедует заметить, что формулы Лапласа плохо работают, в таких случаях, когда вероятность события мала 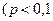 ), а число испытаний в опыте велико. В таких случаях удобно применять асимптотическую формулу Пуассона. Предположим, что в разных сериях испытаний произведение
), а число испытаний в опыте велико. В таких случаях удобно применять асимптотическую формулу Пуассона. Предположим, что в разных сериях испытаний произведение 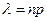 сохра- няет постоянное значение (т.е. среднее число появлений события в различных сериях испытаний при различных значениях
сохра- няет постоянное значение (т.е. среднее число появлений события в различных сериях испытаний при различных значениях 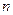 остаётся неизменным). Тогда вероятность того, что при
остаётся неизменным). Тогда вероятность того, что при 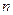 испытаниях событие произойдёт
испытаниях событие произойдёт 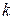 раз вычисляя- ется по формуле Пуассона:
раз вычисляя- ется по формуле Пуассона:
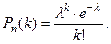 (3)
(3)
Рассмотрим несколько примеров:
Пример 8. Автоматическая телефонная станция в среднем за час получает 300 вызовов. Найти следующие вероятности: а) в данную минуту она получит ровно 3 вызова; б) в данную минуту она получит не менее 3 – х вызовов.
Определим среднее число вызовов в минуту 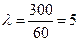 .
.
Тогда, в случае а)
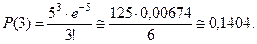
В случае б)
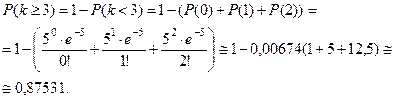
Пример 9. В банк прибыло 2000 пакетов денежных знаков. Вероятность того, что в определённом пакете содержится фальшивый денежный знак, равна 0,0002. Найти вероятность того, что при проверке будет обнаружено: а) ровно 4 фальшивых денежных знака; б) хотя бы один.
По условию, 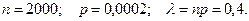
Тогда, в случае а),
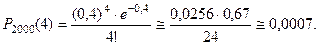
В случае б), 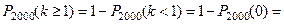
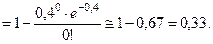
Пример 10. Среди семян пшеницы в среднем имеется 0,2% семян сорняков. Найти вероятность того, что при случайном отборе 3000 семян обнаружится 5 семян сорняков.
По условию, 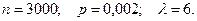 Тогда
Тогда

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
§ 1. ПОНЯТИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ.
В физике и других науках о природе встречается много различных величин разной природы, как например: время, длина, объём, вес и т.д. Постоянной величиной называют ве- личину, принимающую лишь одно фиксированное значение. Величины, которые могут принимать различные значения, на-зываются переменными. Величина считается заданной, если указано множество 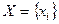 значений, которые она может принимать. Если однозначно известно, какое именно значение из множества
значений, которые она может принимать. Если однозначно известно, какое именно значение из множества 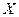 примет величина при создании опреде- лённых условий, то о ней говорят как об «обычной», детерминированной величине. Примером такой величины является количество букв в слове. Большинство физических величин измеряются при помощи приборов с присущей им точностью измерений и, в смысле приведенного определения, они не являются «обычными». Такого рода «необычные» величины называются случайными. Для случайных величин множество
примет величина при создании опреде- лённых условий, то о ней говорят как об «обычной», детерминированной величине. Примером такой величины является количество букв в слове. Большинство физических величин измеряются при помощи приборов с присущей им точностью измерений и, в смысле приведенного определения, они не являются «обычными». Такого рода «необычные» величины называются случайными. Для случайных величин множество 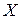 целесообразно назвать множеством возможных значений. Случайная величина принимает то или иное значе- ние с некоторой вероятностью. Заметим, что все величины можно считать случайными, так как детерминированная вели-чина – это случайная величина, принимающая каждое значение с вероятностью, равной единице. Всё сказанное выше является достаточным основанием для изучения случайных величин.
целесообразно назвать множеством возможных значений. Случайная величина принимает то или иное значе- ние с некоторой вероятностью. Заметим, что все величины можно считать случайными, так как детерминированная вели-чина – это случайная величина, принимающая каждое значение с вероятностью, равной единице. Всё сказанное выше является достаточным основанием для изучения случайных величин.
Определение. Случайной величиной называется величина, которая в результате опыта может принимать то или иное (но обязательно только одно) значение, причём заранее, до опыта, неизвестно, какое именно.
Понятие случайной величины является фундаментальным понятием теории вероятностей и играет важную роль в её приложениях.
Случайные величины обозначаются: 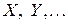 , а их зна -чения, соответственно:
, а их зна -чения, соответственно: 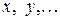 .
.
Выделяют два основных класса случайных величин: диск -ретные и непрерывные.
Определение. Дискретной случайной величиной называют случайную величину, число возможных значений которой конечное либо счётное множество.
Примеры дискретных случайных величин :
1. 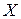 - частота попаданий при трёх выстрелах. Возможные значения:
- частота попаданий при трёх выстрелах. Возможные значения: 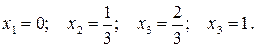
2. 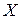 - число деффектных изделий из
- число деффектных изделий из 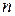 штук. Возможные значения:
штук. Возможные значения: 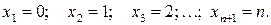
3. 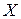 - число выстрелов до первого попадания. Возможные значения:
- число выстрелов до первого попадания. Возможные значения: 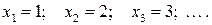
Определение. Непрерывной случайной величиной называют такую случайную величину, возможные значения которой не –прерывно заполняют некоторый промежуток (конечный или бесконечный).
Примеры непрерывных случайных величин:
1. 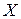 - случайное отклонение по дальности от точки попада- ния до цели при выстреле из орудия.
- случайное отклонение по дальности от точки попада- ния до цели при выстреле из орудия.
Так как снаряд может попасть в любую точку, интервала, ограниченного минимальным и максимальным значениями дальности полёта снаряда, возможных для данного орудия, то возможные значения случайной величины 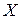 заполняют про -межуток между минимальным и максимальным значением.
заполняют про -межуток между минимальным и максимальным значением.
2. 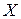 - ошибки при измерении радиолокатором.
- ошибки при измерении радиолокатором.
3. 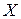 - время работы прибора.
- время работы прибора.
Случайная величина является своего рода абстрактым вы- ражением некоторого случайного события. С каждым случай -ным событием можно связать одну или несколько характеризу- ющих его случайных величин. Например, при стрельбе по ми -шени можно рассмотреть такие случайные величины: число попаданий в мишень, частота попаданий в мишень, количество очков, набираемых при попадании в определённые области мишени и т.д.
§ 2 ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
СЛУЧАЙНЫХ ВЕЛИЧИН.
Определение. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь меж- ду возможными значениями случайной величины и соответст- вующими им вероятностями.
Если вспомнить определение функции, то закон распреде -ления является функцией, область определения которой есть область значений случайной величины, а область значений рассматриваемой функции состоит из вероятностей значений случайной величины.
2.1. РЯД РАСПРЕДЕЛЕНИЯ
Рассмотрим дискретную случайную величину 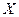 , воз- можные значения которой
, воз- можные значения которой 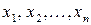 нам известны. Но зна- ние значений случайной величины, очевидно, не позволяет нам её полностью описать, так как мы не можем сказать, насколь- ко часто следует ожидать тех или иных возможных значений случайной величины при повторении опыта в одних и тех же условиях. Для этого необходимо знать закон распределения вероятностей.
нам известны. Но зна- ние значений случайной величины, очевидно, не позволяет нам её полностью описать, так как мы не можем сказать, насколь- ко часто следует ожидать тех или иных возможных значений случайной величины при повторении опыта в одних и тех же условиях. Для этого необходимо знать закон распределения вероятностей.
В результате опыта дискретная случайная величина прини –мает одно из своих возможных значений, т.е. произойдёт одно из событий:
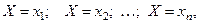 (1)
(1)
которые образуют полную группу несовместных событий.
Вероятности этих событий:
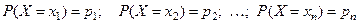 ,
,
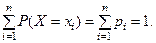
Простейшим законом распределения дискретной случайной величины является таблица, в которой приведены все возмож- ные значения случайной величины и соответствующие им ве –роятности:
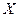
| 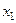
| 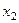
| 
| 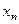
|
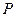
| 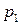
| 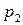
| 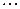
| 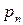
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|