
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Изосова Л.А., Изосов А.В. 7 страница
и её график
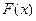
1
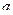
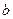
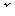
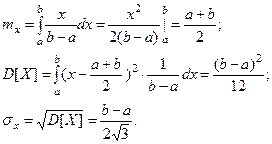
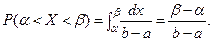
4.6 Показательное распределение.
В практических приложениях теории вероятностей (напри-
мер, в сфере массового обслуживания, исследовании опера -ций, теории надёжности, в физике, биологии и т.п.) часто при- ходится иметь дело со случайными величинами, имеющими так называемое экспоненциальное, или показательное распре- деление.
Определение. Непрерывная случайная ыеличина 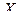 рас- пределена по показательному закону , если её плотность распределения вероятностей имеет вид:
рас- пределена по показательному закону , если её плотность распределения вероятностей имеет вид:
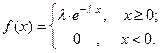
График этой функции:

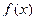
0 
Её функция распределения:

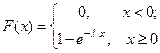 имеет график
имеет график
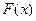
1
О 
Математическое ожидание:
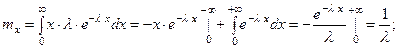
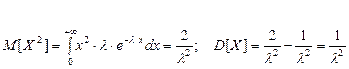
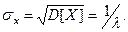
Пример. Пусть случайная величина 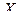 - время работы не- которого механизма, имеет показательное распределение. Оп- ределить вероятность того, что механизм будет работать не менее 1000 часов, если среднее время его работы составляет 800 часов.
- время работы не- которого механизма, имеет показательное распределение. Оп- ределить вероятность того, что механизм будет работать не менее 1000 часов, если среднее время его работы составляет 800 часов.
По условию задачи, математическое ожидание работы меха- низма 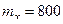 , а
, а 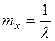 . Тогда
. Тогда 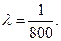
Следовательно, 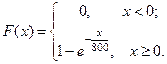
Искомая вероятность:
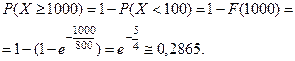
Замечание. Показательное распределение относится к од -нопараметрическим законам распределения (зависит только от 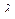 ).
).
4.7 Нормальное распределение.
Определение. Нормальным называют распределение вероят- ностей непрерывной случайной величины, которое имеет плот- ность распределения вероятностей, определяемую формулой:

 (1)
(1)
Видим, что нормальное распределение определяется двумя параметрами :  и
и 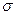 . Чтобы задать нормальное распре -деление, достаточно задать эти два параметра.
. Чтобы задать нормальное распре -деление, достаточно задать эти два параметра.
Нормальный закон распределения очень широко распро- странён в задачах практики. Он проявляется в тех случаях, когда случайная величина 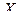 является результатом действи- ем большого числа различных факторов. Каждый фактор в отдельности влияет на случайную величину незначительно и нельзя сказать, какой из них влияет в большей степени, чем остальные. Примерами случайных величин, имеющих нормаль- ное распределение, можно считать: отклонение размеров дета- лей, изготовленных станком, от стандартных; ошибки при из -мерении; отклонения при стрельбе по мишени и т.п.
является результатом действи- ем большого числа различных факторов. Каждый фактор в отдельности влияет на случайную величину незначительно и нельзя сказать, какой из них влияет в большей степени, чем остальные. Примерами случайных величин, имеющих нормаль- ное распределение, можно считать: отклонение размеров дета- лей, изготовленных станком, от стандартных; ошибки при из -мерении; отклонения при стрельбе по мишени и т.п.
Основной закономерностью, выделяющей нормальный закон из остальных законов, является та, что он является предель -ным законом, к которому приближаются другие законы, т.е. при достаточно большом значении  сумма независимых слу- чайных величин
сумма независимых слу- чайных величин 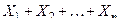 , подчинённых каким угодно законам распределения, будет иметь распределение, сколь угодно близкое к нормальному.
, подчинённых каким угодно законам распределения, будет иметь распределение, сколь угодно близкое к нормальному.
Функция распределения нормально распределённой случай –ной величины имеет вид
 (2)
(2)
По определению математического ожидания непрерывной случайной величины,
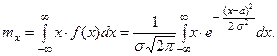
Введём новую переменную
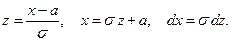
Принимая во внимание, что новые пределы интегрирования равны старым, получим
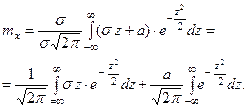
Первой слагаемое равно нулю, как интеграл по симметрич -ному промежутку от нечётной функции. Второе из слагаемых равно  (интеграл Пуассона
(интеграл Пуассона 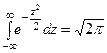 ).
).
Таким образом, математическое ожидание нормально рас- пределённой случайной величины 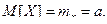
По определению дисперсии непрерывной случайной величи- ны, учитывая, что 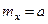 , получим
, получим
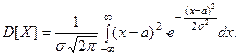
Снова введём новую переменную
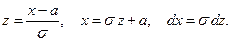
Получим 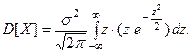 Применив формулу интегрирования по частям и предыдущие вычисления, получа- ем
Применив формулу интегрирования по частям и предыдущие вычисления, получа- ем 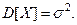 Тогда
Тогда 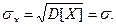 Следовательно, вторым параметром нормального распределения является сре- днее квадратическое отклонение.
Следовательно, вторым параметром нормального распределения является сре- днее квадратическое отклонение.
Замечение. Нормированным называют нормальное распре –деление с параметрами 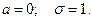 Плотность нормиро -ванного распределения задаётся функцией:
Плотность нормиро -ванного распределения задаётся функцией:
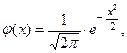 (3)
(3)
значения которой можно либо найти непосредмьвенно, либо воспользоватся соответствующими таблицами, которые можно найти во всех справочниках. Функция нормированного распре –деления имеет вид 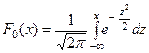 . Тогда функция общего нормального распределения, заданная т формулой (2), выражается формулой
. Тогда функция общего нормального распределения, заданная т формулой (2), выражается формулой 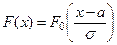 . Вероятность попа- дания нормированной нормально распределённой случайной величины
. Вероятность попа- дания нормированной нормально распределённой случайной величины 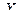 в интервал
в интервал 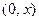 определяется с помощью функции Лапласа
определяется с помощью функции Лапласа 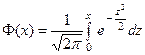 , значения которой также приведены в таблицах. В самом деле,
, значения которой также приведены в таблицах. В самом деле,
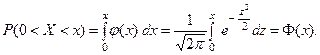
Учитывая, что 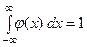 (по свойству плотности распре- деления,), в силу симметрии функции
(по свойству плотности распре- деления,), в силу симметрии функции 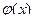 относительно точ- ки
относительно точ- ки 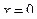 :
: 
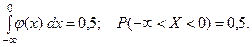
Тогда 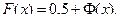
График плотности нормального распределения называют нормальной кривой или кривой Гаусса.
Исследуем функцию: 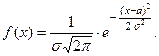
Она определена на всей числовой прямой и положительна для всех  . При неограниченном возрастании
. При неограниченном возрастании  данная функция стремится к нулю, т.е.
данная функция стремится к нулю, т.е. 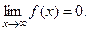 Производная этой функции
Производная этой функции 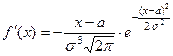 .
.
Производная равна 0 в точке 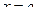 и меняет в этой точке знак с «+» на «-», т.е.
и меняет в этой точке знак с «+» на «-», т.е. 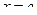 - точка максимума и в этой точке
- точка максимума и в этой точке 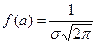 . Найдя вторую производную функции, можем выяснить, что график функции имеет перегибы в точ- ках
. Найдя вторую производную функции, можем выяснить, что график функции имеет перегибы в точ- ках 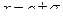 . Схематически график выглядит следующим образом:
. Схематически график выглядит следующим образом:
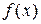

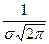
0 

Для нормально распределенной случайной величины ве- роятность попадания в заданный интервал 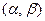 вычисля –ется следующим образом:
вычисля –ется следующим образом:
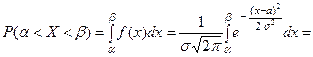
Сделаем замену 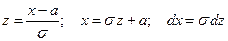 .
.
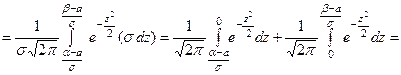
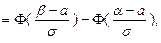 где
где 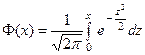 .
.
Таким образом,
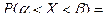
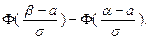 (4)
(4)
Пример. Масса вагона - случайная величина, распределён -ная по нормальному закону с математическим ожиданием 65 т. и средним квадратическим отклонением 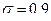 т. Найти веро- ятность того, что очередной вагон имеет массу не более 70 т. и не менее 60 т
т. Найти веро- ятность того, что очередной вагон имеет массу не более 70 т. и не менее 60 т
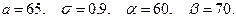
Тогда
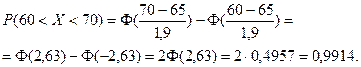
Иногда требуется вычислить вероятность того, что случай -ная величина по модулю отклоняется от среднего значения меньше чем некоторое значение 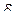 , т.е.
, т.е. 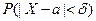 . Для вычисления этой вероятности можем воспользоваться предыдущей формулой. В самом деле:
. Для вычисления этой вероятности можем воспользоваться предыдущей формулой. В самом деле:
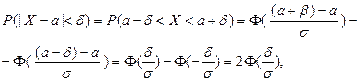
учитывая нечётность функции 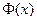 . Следовательно,
. Следовательно,
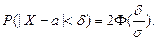 (5)
(5)
Пример. Вероятность того, что нормально распределённая случайная с математическим ожиданием 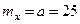 откло- нится от среднего значения меньше чем на
откло- нится от среднего значения меньше чем на 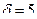 равна 0.09. Чему равна вероятность попадания этой случайной величины в интервал (30, 35) ?
равна 0.09. Чему равна вероятность попадания этой случайной величины в интервал (30, 35) ?
По условию, 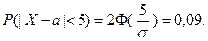 Тогда
Тогда 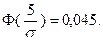 По таблице значений функции Лапласа, по – лучаем:
По таблице значений функции Лапласа, по – лучаем: 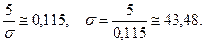 Тогда требуемая вероятность , по формуле (4),
Тогда требуемая вероятность , по формуле (4),
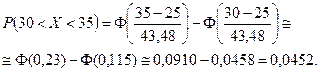
Правило трёх сигм.
В формуле (5) положим 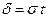 , получим
, получим
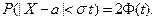
Если 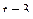 и, следовательно,
и, следовательно, 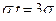 , получаем:
, получаем:
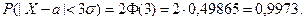
т.е. вероятность того, что отклонение по абсолютной величине случайной величины от среднего значения меньше утроенного среднего квадратического отклонения равна 0,9973, т.е. очень близка к единице.
Правило трёх сигм состоит в том, что для нормально рас- пределённой случайной величины абсолютная величина её -отклонения от среднего не превосходит утроенного сред -него квадратического отклонения. На практике это правило применяется слудующим образом: Если распределение слу -чайной величины неизвестно, но для её параметров выпол -няется правило трёх сигм, то есть основание предположить, что она распределена по нормальному закону.
§ 5. ЗАКОН БОЛЬШИХ ЧИСЕЛ И ПРЕДЕЛЬНЫЕ
ТЕОРЕМЫ.
Известно, что нельзя заранее предсказать, какое именно значение примет случайная величина в результате некоторого испытания, так как это зависит от очень многих случайных причин, учесть влияние которых невозможно. Но оказывается, что при некоторых условиях суммарное поведение достаточно большого числа случайных величин почти утрачивает случай -ный характер и становится закономерным.
Под законом больших чисел в широком смысле понимается общий принцип, согласно которому, по формулировке академи- ка А.Н. Колмогорова, совокупное действие большого числа случайных факторов (при некоторых общих условиях) приво – дит к результату, почти независимому от случая. Другими словами, при большом числе случайных величин их средний результат перестаёт быть случайным и может быть предсказан с большой степенью определённости.
Приведём без доказательства несколько теорем, в которых устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определённым посто -янным.
5.1 Неравенство Маркова (лемма Чебышева).
ТЕОРЕМА. Если случайная величина 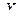 принимает только положительные значения с некоторым математическим ожида –нием
принимает только положительные значения с некоторым математическим ожида –нием 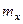 , то для любого положительного числа
, то для любого положительного числа 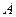 выполня - ется неравенство:
выполня - ется неравенство: 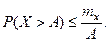
Или, то же неравенство Маркова в другой форме:
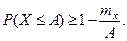
Неравенства Маркова применимы для любых неотрицатель- ных случайных величин.
Пример. Сумма всех вкладов в некотором отделении сбер- банка составляет 4 млн. рублей, а вероятность того, что слу -чайно выбранный вклад не превышает 40 тыс. рублей, равна 0,7. Что можно сказать о числе вкладчиков?
Пусть 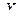 - величина случайно выбранного вклада, а
- величина случайно выбранного вклада, а  - число всех вкладов. Тогда, по условию задачи,
- число всех вкладов. Тогда, по условию задачи, 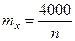 (тыс. рублей). Тогда, по второму неравенству Маркова,
(тыс. рублей). Тогда, по второму неравенству Маркова,
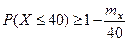 , или
, или 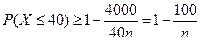 .
.
Так как 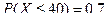 , то
, то 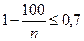 , или
, или 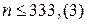 , т.е. число вкладчиков не более 333.
, т.е. число вкладчиков не более 333.
5.2 Неравенство Чебышева.
ТЕОРЕМА. Для любой случайной величины, имеющей мате- тическое ожидание 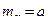 и дисперсию
и дисперсию 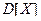 при
при 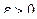 выполняется неравенство:
выполняется неравенство: 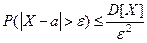 , (1)
, (1)
или соответственно,  (2)
(2)
Пример. Средний расход электроэнергии на некотором предприятии равен 2000 кв. в день, а среднее квадратическое отклонение расхода не превосходит 400 кв. Используя нера -венство Чебышева, оценить вероятность того, что в любой день расход электроэнергии не превзойдёт 4000 кв.
В данном случае дисперсия 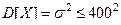 . Так как границы интервала
. Так как границы интервала 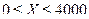 симметричны относительно математического ожидания
симметричны относительно математического ожидания 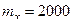 , то для оценки требу- емой вероятности можно использовать неравенство Чебышева.
, то для оценки требу- емой вероятности можно использовать неравенство Чебышева.
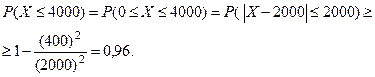
Неравенство Чебышева применимо для любых случайных величин. В форме (1) оно устанавливает верхнюю, а в фор- ме (2) нижнюю границу вероятности рассматриваемого со- бытия.
Если мы рассматриваем дискретную случайную величину 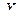 , принимающую значения
, принимающую значения 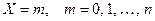 ,
,
вероятности каждого из которых вычисляются по формуле Бернулли, т.е. имеющую биномиальное распределение, то 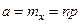 ,
, 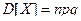 , и неравенство Чебышева приоб- ретает вид:
, и неравенство Чебышева приоб- ретает вид: 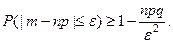 (3)
(3)
Для частоты 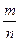 события в серии из
события в серии из  независимых испы- таний, в каждом из которых оно может произойти с одной и той же вероятностью
независимых испы- таний, в каждом из которых оно может произойти с одной и той же вероятностью 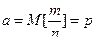 , и имеющей дисперсию
, и имеющей дисперсию 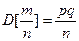 , вероятность отклонения относительной частоты события от его вероятности оценивается с помощью формулы:
, вероятность отклонения относительной частоты события от его вероятности оценивается с помощью формулы:

Пример. Вероятность появления события в каждом незави -симом испытании равна 0,4. Используя неравенство Чебышева,
Оценить вероятность того, что при 100 независимых испыта –ниях число появлений события заключено в промежутке от 30 до 50.
 . Требуемое число появлений события представляет собой про -межуток, симметричный относительно математического ожи –дания. Тогда
. Требуемое число появлений события представляет собой про -межуток, симметричный относительно математического ожи –дания. Тогда 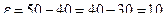 . По формуле (3) получаем
. По формуле (3) получаем 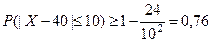 .
.
5.3 Теорема Чебыщева.
ТЕОРЕМА. Если последовательность попарно независимых случайных величин 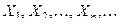 имеет конечные мате- матические ожидания и дисперсии этих случайных величин равномерно ограничены (не превышают некоторого постоянного значения
имеет конечные мате- матические ожидания и дисперсии этих случайных величин равномерно ограничены (не превышают некоторого постоянного значения 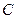 ), то среднее арифметическое этих случайных ве –личин сходится по вероятности к среднему арифметическому их математических ожиданий, т.е. для любого
), то среднее арифметическое этих случайных ве –личин сходится по вероятности к среднему арифметическому их математических ожиданий, т.е. для любого 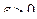
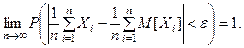 (4)
(4)
В этой теореме предполагалось, Что сучайные величины имеют различные математические ожидания, но на практике чаще бывает, что в последовательности испытаний случайные величины имеют одно и тоже математическое ожидание и дис- персии их равномерно ограничены. В этом случае формула (4) приобретает вид:
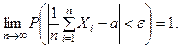 (5)
(5)
Теорема Чебышева справедлива как для дискретных, так и для непрерывных случайных величин.
Сущность теоремы Чебышева состоит в том, что среднее арифметическое достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограни- чены) утрачивает характер случайной величины.
На теореме Чебышева основан широко применяемый в ста- тистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке элементов не -которой совокупности судят о поведении всей совокупности (генеральной совокупности). Например, при проверке качества каких – либо изделий проверяется некоторое количество слу - чайно взятых деталей.
Пример. Для проверки средней продолжительности службы электроламп в партии тз 400 одинаковых ящиков по выбору взяли по одной лампе из каждого ящика. Оценить вероятность того, что средняя продолжительность службы 400 электроламп отличается от средней продолжительности службы электро -ламп из всей партии не более чем на 5 ч. (по абсолютной ве- личине), если известно, что среднее квадратическое отклоне -ние продолжительности службы электроламп для каждого ящи- ка меньше чем 8 часов.
Пусть 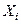 - продолжительность службы электролампы, взя- той из
- продолжительность службы электролампы, взя- той из 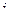 - го ящика. По условию,
- го ящика. По условию, 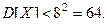 Очевидно, что средняя продолжительность службы отобранных элек- троламп равна
Очевидно, что средняя продолжительность службы отобранных элек- троламп равна 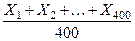 , а средняя продолжи -тельность службы электроламп из всей партии равна
, а средняя продолжи -тельность службы электроламп из всей партии равна
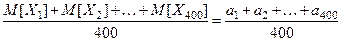 .
.
Тогда вероятность искомого события
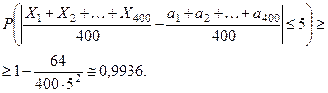
5.4 Теорема Бернулли.
ТЕОРЕМА. Пусть произведены  независимых испытаний,
независимых испытаний,
в каждом из которых постоянна вероятность появления собы -тия 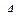 :
: 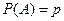 . Тогда при неограниченном числе испыта- ний отклонение относительной частоты события от его веро –ятности имеет свойство:
. Тогда при неограниченном числе испыта- ний отклонение относительной частоты события от его веро –ятности имеет свойство:
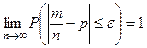
для любого 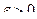 .
.
Другими словами, теорема Бернулли утверждает, что при  относительная частота события стремится «по вероят- ности» к истинной вероятности этого события.
относительная частота события стремится «по вероят- ности» к истинной вероятности этого события.
5.5 Центральная предельная теорема.
Закон больших чисел устанавливает факт приближения среднего значения большого числа случайных величин к оп -ределённым постоянным значениям. Более того, оказывается, что при некоторых условиях совокупное действие случайных величин приводит к определённому, а именно к нормальному закону распределения.
Центральная предельная теорема представляет собой группу теорем, посвящённых установлению условий, при ко –торых возникает нормальный закон распределения. Среди этих теорем важнейшее значение принадлежит теореме Ляпунова.
ТЕОРЕМА ЛЯПУНОВА. Если 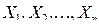 - независи - мые случайные величины, для каждой из которых математи – ческое ожидание
- независи - мые случайные величины, для каждой из которых математи – ческое ожидание 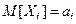 , дисперсия
, дисперсия 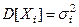 , абсо- лютный центральный момент 3 – го порядка
, абсо- лютный центральный момент 3 – го порядка
 и
и 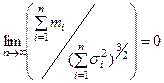 , (6)
, (6)
то закон распределения суммы 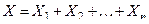 при
при  неограниченно приближается к нормальному закону с матема -тическим ожиданием
неограниченно приближается к нормальному закону с матема -тическим ожиданием 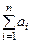 и дисперсией
и дисперсией  . Условие (6) состоит в том, что в сумме
. Условие (6) состоит в том, что в сумме 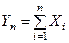 не должно быть слагаемых, влияние которых на сумму было бы подав -ляюще высоко, по сравнению с остальными, т.е. «удельный вес» каждого слагаемого должен стремиться к нулю при увели- чении числа слагаемых.
не должно быть слагаемых, влияние которых на сумму было бы подав -ляюще высоко, по сравнению с остальными, т.е. «удельный вес» каждого слагаемого должен стремиться к нулю при увели- чении числа слагаемых.
Так например, потребление электроэнергии для бытовых нужд в каждой квартире многоквартирного дома можно пред- ставить в виде суммы 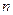 различных случайных величин. Если потребление электроэнергии в каждой квартире не выделяется резко среди остальных, то, на основании теоремы Ляпунова,
различных случайных величин. Если потребление электроэнергии в каждой квартире не выделяется резко среди остальных, то, на основании теоремы Ляпунова,
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|