
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Изосова Л.А., Изосов А.В. 5 страница
Такую таблицу называют рядом распределения случайной величины 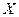 .
.
Для наглядности, ряд распределения можно представить графиком:
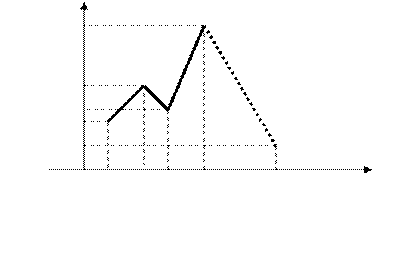
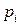
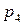
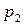
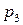
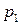
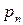
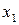
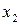
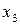
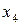
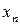
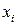
Эта ломаная называется многоугольником распределения. Это также одна из форм задания закона распределения дискрет – ной случайной величины 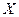 .
.
Сумма ординат многоугольника распределения, представля – ющая сумму вероятностей всех возможных значений случай -ной величины, равна единице.
Пример 1. Произведено три выстрела по мишени. Вероят- ность попадания при каждом выстреле равна 0,7. Составить ряд распределения числа попаданий.
Случайная величина 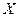 - «число попаданий» может прин- мать значения от 0 до 3 – х, причём в этом случае вероят – ности определяются по формуле Бернулли:
- «число попаданий» может прин- мать значения от 0 до 3 – х, причём в этом случае вероят – ности определяются по формуле Бернулли:
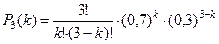 .
.
Тогда 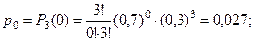
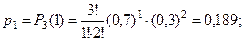
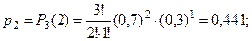
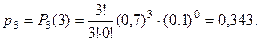
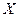
| 0 | 1 | 2 | 3 |
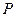
| 0,027 | 0,189 | 0,441 | 0,343 |
Проверка 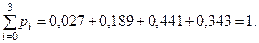
Пример 2. В урне назодится 4 белых и 6 чёрных щаров. Наугад извлекаются 4 шара. Найти закон распределения слу- чайной величины 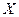 - «число белых шаров среди отобран -ных».
- «число белых шаров среди отобран -ных».
Эта случайная величина может принимать значения от 0 до 4 – х. Найдём вероятности аозможных значений случайной величины.

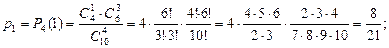
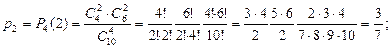
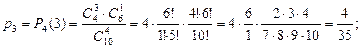
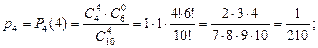
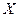
| 0 | 1 | 2 | 3 | 4 |
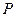
| 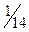
| 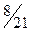
| 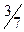
| 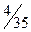
| 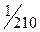
|
Можем проверить, что сумма полученных вероятностей рав- на единице.
2.2. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ.
Ряд распределения нельзя построить для непрерывной слу- чайной величины, так как она принимает бесконечно много значений. Более универсальным законом распределения под- ходящим, как для дискретной, так и для непрерывной слу - чайной величины 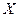 является функция распределения.
является функция распределения.
Определение. Функцией распределения (интегральным зако- ном распределения) случайной величины 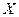 называется зада- ние вероятности выполнения неравенства
называется зада- ние вероятности выполнения неравенства 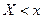 , т.е.
, т.е.
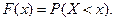 (1)
(1)
Таким образом, функция распределения 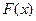 равна вероят -ности того, что случайная величина в результате опыта попа- дает левее точки
равна вероят -ности того, что случайная величина в результате опыта попа- дает левее точки 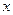 .
.
Для дискретной случайной величины, для которой мы знаем ряд распределения:
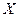
| 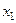
| 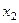
| 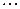
| 
|
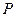
| 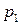
| 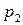
| 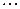
| 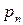
|
функция распределения будет иметь вид:
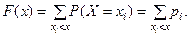
График функции распределения дискретной случайной вели- чины - разрывная ступенчатая фигура. Для наглядности, рассмотрим пример.
Пример 3 Дан ряд паспределения. Найти функцию распре -деления и построить её график
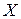
| 1 | 2 | 3 | 4 |
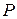
| 0,2 | 0,1 | 0,3 | 0,4 |
По определению,
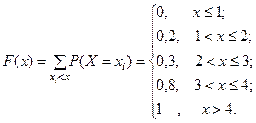
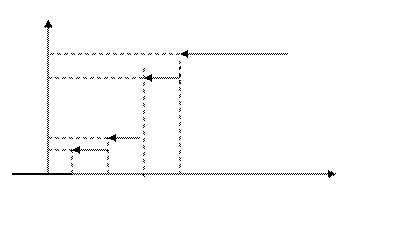
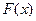
1
0,8
0,3
0,2
1 2 3 4 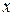
СВОЙСТВА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
1 Функция распределения - это неотрицательная фун- кция, значения которой заключены между 0 и 1, т.е. 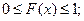
2 Вероятность появления случайной величины в про- межутке 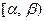 равна разности значений функции распределения на концах промежутка:
равна разности значений функции распределения на концах промежутка:
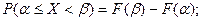 (2)
(2)
3 Функция распределения - неубывающая функция, т.е. при 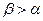 выполнено:
выполнено:  ;
;
4 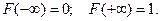
Перейдём в равенстве (2) к пределу при  . Полу- чим вместо вероятности попадания случайной величины в про- межуток
. Полу- чим вместо вероятности попадания случайной величины в про- межуток 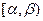 вероятность точечного значения случайной величины, т.е.
вероятность точечного значения случайной величины, т.е.
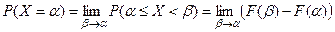 . (3)
. (3)
Значение этого предела зависит от того, является ли точка 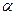 точкой непрерывности функции
точкой непрерывности функции 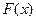 , или в этой точке функция
, или в этой точке функция 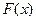 имеет разрыв. Если функция
имеет разрыв. Если функция 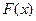 непрерыв- на в точка
непрерыв- на в точка 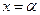 , то предел равен 0, т.е.
, то предел равен 0, т.е. 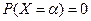 . Если же в этой точке функция
. Если же в этой точке функция 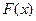 имеет разрыв (1 – го ро- да), то предел равен значению скачка функции
имеет разрыв (1 – го ро- да), то предел равен значению скачка функции 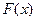 в точке
в точке 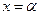 .
.
Так как непрерывная случайная величина имеет непрерыв -ную функцию распределения  , то из равенства нулю предела (3) следует, что вероятность любого фиксированного значения непрерывной случайной величины равна нулю. Это следует из того, что возможных значений непрерывной случайной величины бесконечно много. Из этого, в частности, следует, что следующие вероятности совпадают:
, то из равенства нулю предела (3) следует, что вероятность любого фиксированного значения непрерывной случайной величины равна нулю. Это следует из того, что возможных значений непрерывной случайной величины бесконечно много. Из этого, в частности, следует, что следующие вероятности совпадают:
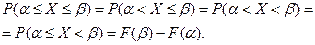
Приведённые свойства функции распределения можно сфор- мулировать следующим образом: функция распределения - это неотрицательная неубывающая функция, удовлетворяющая ус –ловиям: 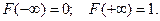 Обратное утверждение также имеет место: монотонно возрастающая непрерывная функция, удовлетворяющая условиям
Обратное утверждение также имеет место: монотонно возрастающая непрерывная функция, удовлетворяющая условиям
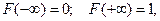
является функцией распределения некоторой непрерывной слу- чайной величины. Если значения этой величины сосредоточе -ны на некотором промежутке 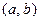 , то график этой функции можно схематически изобразить следующим образом:
, то график этой функции можно схематически изобразить следующим образом:
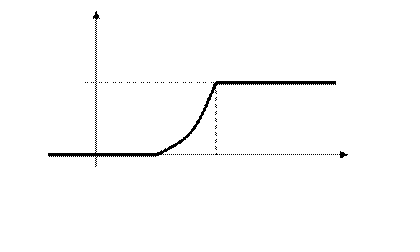
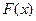
1
0 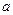
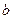
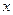
Рассмотрим пример. Функция распределения непрерывной случайной величины 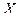 задана следующим образом:
задана следующим образом:
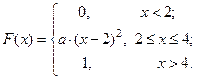
Найти значение « 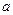 », построить график
», построить график 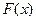 и найти веро –ятность
и найти веро –ятность 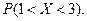
Так как функция распределения непрерывной случайной ве- личины непрерывна, то 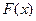 - непрерывная функция, и при
- непрерывная функция, и при 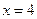 должно выполгяться равенство:
должно выполгяться равенство:
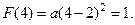 или
или 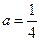 , т.е.
, т.е.
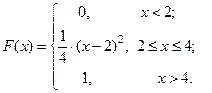
Построим график этой функции
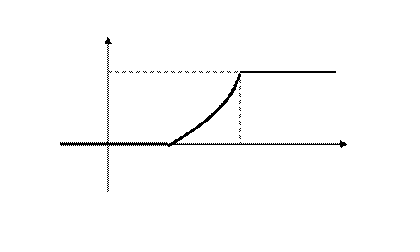
1
0 2 4 
Найдём требуемую вероятность
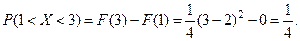
Замечание. Функцию распределения, иногда ещё называют интегральным законом распределения. Ниже объясним, почему именно.
2.3 ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ.
Так как с помощью функции распределения дискретной
случайной величины в любой точке мы можем определить вероятность возможных значений, то она однозначно опре- деляет закон распределения дискретной случайной величины.
Однако по функции распределения трудно судить о харак- тере распределения непрерывной случайной величины в не -большой окрестности той или иной точки числовой оси.
Более наглядное представление о характере распределения непрерывной случайной величины вблизи различных точек даёт функция, которую называют плотностью распределения (или дифференциальным законом распределения)
Пусть  - непрерывная случайная величина с функцикй распределения
- непрерывная случайная величина с функцикй распределения 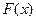 . Найдём вероятность попадания этой случайной величины в элементарный участок
. Найдём вероятность попадания этой случайной величины в элементарный участок 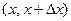 .
.
По формуле (2), имеем
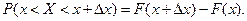
Разделим это равенство на 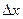
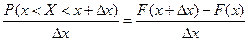 .
.
Отношение, стоящее слева, называется средней вероятно –стью на единице длины участка.
Считая функцию 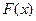 дифференцируемой, перейдём к перейдём в этом равенстве к пределу
дифференцируемой, перейдём к перейдём в этом равенстве к пределу
 .
.
Определение. Предел отношения вероятности попадания непрерывной случайной величины на элементарный участок 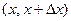 к длине этого участка
к длине этого участка 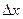 при
при 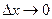 называ- ется плотностью распределения непрерывной случайной ве – личины
называ- ется плотностью распределения непрерывной случайной ве – личины  и обозначается
и обозначается 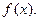 Следовательно,
Следовательно,
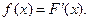
Плотность распределения показывает, насколько часто слу -чайная величина 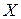 появляется в некоторой окрестности точ –ки
появляется в некоторой окрестности точ –ки 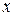 при повторении опытов.
при повторении опытов.
Кривая, изображающая график плотности распределения, на- зывается кривой распрелеления.
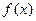
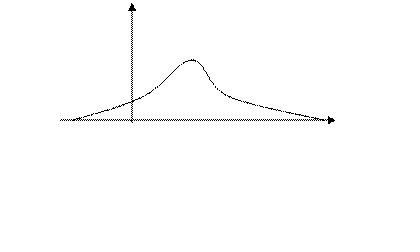
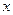
Если возможные значения случайной величины 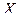 запол- няют некоторый промежуток
запол- няют некоторый промежуток 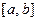 , то
, то 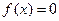 вне этого промежутка.
вне этого промежутка.
Определение. Случайная величина 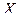 называется непре – рывной, если её функция распределения
называется непре – рывной, если её функция распределения 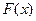 непрерывна на всей числовой прямой, а плотность распределения
непрерывна на всей числовой прямой, а плотность распределения 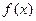 не- прерывна везде, за исключением может быть конечного числа точек (точек разрыва 1 – го рода).
не- прерывна везде, за исключением может быть конечного числа точек (точек разрыва 1 – го рода).
СВОЙСТВА ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ
1. Плотность распределения неотрицательна, т.е. 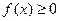
(это следует из того, что 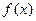 - производная неубывающей функции
- производная неубывающей функции 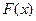 ).
).
2. Функция распределения непрерывной случайной величи-
ны равна интегралу от плотности распределения ( и поэтому является интегральным законом распределения), т.е.
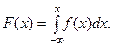
В самом деле, 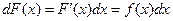 (по определению дифференциала функции). Следовательно,
(по определению дифференциала функции). Следовательно,
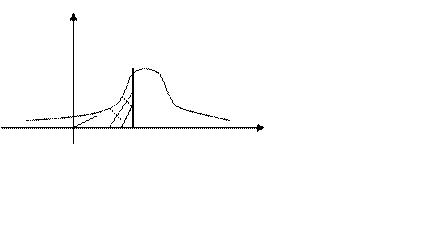
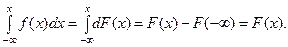
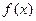
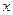
На графике плотности распределения функция распределения
изображается площадью заштрихованной области.
3. Вероятность попадания случайной величины на участок  равна интегралу от плотности распределения по этому промежутку, т.е.
равна интегралу от плотности распределения по этому промежутку, т.е. 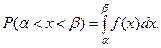
В самом деле,
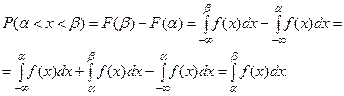
4. Интеграл в бесконечных пределах от плотности распре –деления равен единице, т.е.
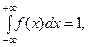
Другими словами, площадь фигуры под графиком плотности распределения равна 1. В частности, если возможные значе- ния случайной величины сосредоточены на участке 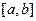 , то
, то
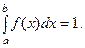
Пример. Пусть плотность распределения зазана функцией
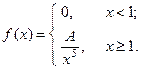
Найти: а) значение параметра 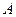 ; б) функцию распределения
; б) функцию распределения 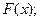 в) Вычислить вероятность того, что случайная величи- на примет значение из отрезка
в) Вычислить вероятность того, что случайная величи- на примет значение из отрезка 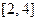 .
.
а) По свойству 4, 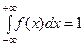 . Тогда
. Тогда
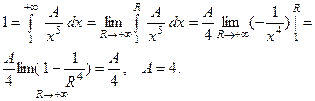
б) По свойству 2, 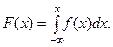 Если
Если 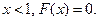
Если 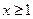 ,
, 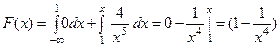 .
.
Таким образом,
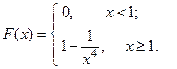
в) По свойству 3,
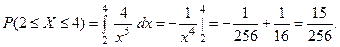
§ 3. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ
ВЕЛИЧИН
При решении многих практических задач нет необходимости знать все вероятностные характеристики случайной величины. Иногда достаточно знать только некоторые числовые характе - ристики закона распределения.
Числовые характеристики позволяют в сжатой форме выра -зить наиболее существенные особенности того или иного рас- пределения.
О каждой случайной величине прежде всего необходимо знать её среднее значения, около которого группируются все возможные значения этой величины, а также некоторое число, характеризующее степень рассеяния этих значений относитель- но среднего.
Различают характеристики положения и характеристики рас- сеяния. Одной из самых важных характеристик положения яв- ляется математическое ожидание.
3.1 Математическое ожидание (среднее значение).
Рассмотрим сначала дискретную случайную величину, име -ющую возможные значения 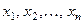 с вероятностями
с вероятностями
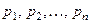 .
.
Определение. Математическим ожиданием дискретной слу- чайной величины 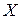 называется сумма произведений всех возможных значений этой величины на их вероятности, т.е.
называется сумма произведений всех возможных значений этой величины на их вероятности, т.е.
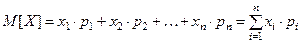 . (1)
. (1)
По другому, математическое ожидание обозначается
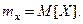
Пример. Пусть дан ряд распределения:
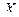
| 1 | 2 | 3 | 4 |
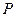
| 0,2 | 0,1 | 0,3 | 0,4 |
Тогда 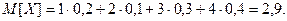
Рассмотрим теперь непрерывную случайную величину 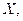 все возможные значения которой заключены в отрезке
все возможные значения которой заключены в отрезке 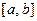 .
.
Разобьём этот отрезок на 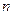 частичных отрезков, длины которых обозначим:
частичных отрезков, длины которых обозначим: 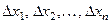 , и в каждом частичном интервале возьмём по произвольной точке, соответственно
, и в каждом частичном интервале возьмём по произвольной точке, соответственно 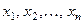 .
.
Так как произведение 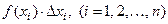 при- ближённо равно вероятности попадания случайной величины на элементарный участок
при- ближённо равно вероятности попадания случайной величины на элементарный участок 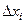 , то сумма произведений
, то сумма произведений 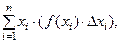 составленная по аналогии с опреде -лением математического ожидания дискретной случайной ве- личины, приближённо равна математическому ожиданию не -прерывной случайной величины
составленная по аналогии с опреде -лением математического ожидания дискретной случайной ве- личины, приближённо равна математическому ожиданию не -прерывной случайной величины 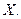 Пусть
Пусть 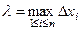 .
.
Тогда 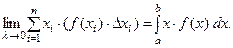
Определение. Математическим ожиданием непрерывной случайной величины называется следующий определённый интеграл:
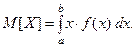 (2)
(2)
Если непрерывная случайная величина принимает значения на всей числовой прямой, то 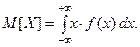
Пример. Пусть дана плотность распределения непрерывной случайной величины:
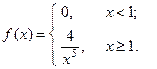
Тогда её математическое ожидание:
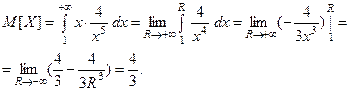
Понятие математического ожидания имеет простую меха -ническую интерпретацию. Распределение вероятностей слу -чайной величины можно интерпретироварь как распределение единичной массы по прямой. Дискретной случайной величине, принимающей значения 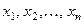 с вероятностями
с вероятностями 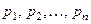 соответствует прямая, на которой массы
соответствует прямая, на которой массы 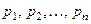 сосредоточены в точках
сосредоточены в точках 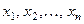 . Непре- рывной случайной величине отвечает непрерывное распреде -ление масс на всей прямой или на конечном отрезке этой прямой. Тогда математическое ожидание - это абсцисса цент- ра тяжести.
. Непре- рывной случайной величине отвечает непрерывное распреде -ление масс на всей прямой или на конечном отрезке этой прямой. Тогда математическое ожидание - это абсцисса цент- ра тяжести.
СВОЙСТВА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ
1. Математическое ожидание постоянной величины равно самой постоянной: 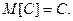
2. Постоянный множитель можно вынести за знак матема- тического ожидания: 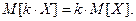
3. Математическое ожидание алгебраической суммы слу –чайных величин равна алгебраической сумме их мате- матических ожиданий: 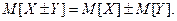
4. Математическое ожидание произведения независимых случайных величин равно произведению их математи -ческих ожиданий: 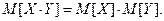
5. Математическое ожидание отклонения случайной вели- чины от её математического ожидания равно нулю: 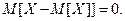
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|