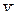Изосова Л.А., Изосов А.В. 8 страница

можно считать, что потребление электроэнергии всего дома (т.е. суммарный закон распределения) будет иметь приближён- но нормальный закон распределения. Но если в некотором помещении этого дома расположена, к примеру мастерская по ремонту электрооборудования, работа которой связана с боль -шим расходом электроэнергии, то вывод о нормальном распре- делении электроэнергии в этом доме будет неверным, так как нарушено условие (6) теоремы Ляпунова.

§ 6. ФУНКЦИЯ ОДНОГО СЛУЧАЙНОГО АРГУМЕНТА ЕЁ

РАСПРЕДЕЛЕНИЕ И МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ

Если каждому значению случайной величины 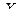соответ- ствует одно из возможных значений случайной величины 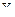, то 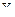называют функцией случайного аргумента :

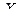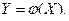
6.1. Пусть 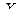- дискретная случайная величина.

а) Если различным значениям случайной величины 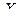отве- чают различные значения случайной величины 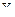, то вероят -ности соответствующих значени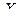й и 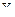равны между собой.

Пример 1. Дискретная случайная величина 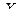задана рядом распределения:

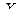
	- 2	-1	0	1	2
	0,2	0,1	0,1	0,3	0,3

Тогда закон распределения функции 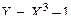задаётся рядом:

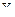
	- 9	-2	-1	0	7
	0,2	0,1	0,1	0,3	0,3

б) Если различным значениям 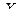отвечают значения случай- ной величины 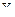, среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений .

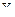Пример 2. Пусть случайная величина 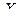задана тем же рядом распределения:

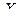
	- 2	-1	0	1	2
	0,2	0,1	0,1	0,3	0,3

Тогда ряд распределения случайной величины 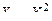имеет вид:

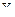
	0	1	4
	0,1	0,4	0,5

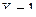( при , поэтому складываем соответствующие вероятности 0,1+0,3=0,4; 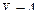при , поэтому скла- дываем вероятности 0,2+0,3=0,5).

6.2. Пусть теперь 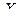- непрерывная случайная величина,

заданная плотностью распределения 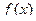. Пусть функция 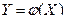- дифференцируемая и сторого монотонная, т.е. имеет дифференцируемую обратную функцию 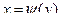. Тог -да плотность распределения случайной величины 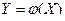гаходится с помощью равенства:

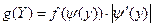Пример 3. Пусть случайная величина 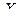распределена по закону Коши

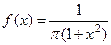Найти плотность распределения случайной величины .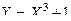

Обратная функция 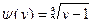. Эта функция строго монотонна и дифференцируема

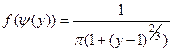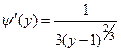. Тогда плотность распределения случай- ной величины 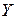имеет вид:

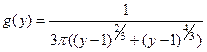Если функция 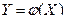в интервале возможных значений 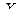не монотонна, то стоит разбить этот интервал на интер- валы, в каждом из которых функция 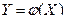является мо- нотонной, найти 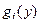для каждого из интервалов монотон –ности и затем представить 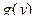в виде суммы:

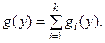
Пример 4. Задана плотность распределения нормально распределённой случайной величины :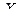

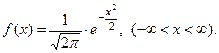
Найти плотность распределения 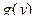случайной величины .

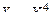Из уравнения 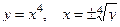. Так как на промежетке 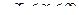функция 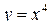не монотонна, то обратная функция состоит из двух частей. На промежутке ,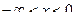

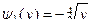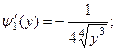
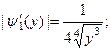
На промежутке

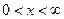
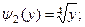
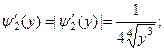
Тогда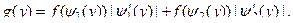

, .

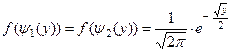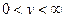Тогда

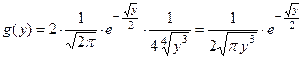
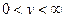и вне этого интервала.

6.3. Пусть 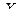- дискретная случайная величина с возмож -

ными значениями 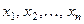, вероятности которых равны соответственно: 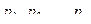. Функция 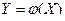также дискретная случайная величина, причём свои возможные зна- чения 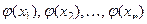она принимает с теми же ве- роятностями 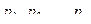. Тогда её математическое ожи- дание вычисляется по формуле:

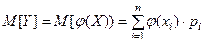Пример 5 Пусть дискретная случайная величина задана рядом распределения:

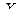
	- 2	-1	0	1	2
	0,2	0,1	0,1	0,3	0,3

Найти математическое ожидание случайной величины

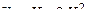. Это также дискретная случайная величина с рядом распределения:

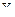
	- 10	- 3	0	-1	- 6
	0,2	0,1	0,1	0,3	0,3

Тогда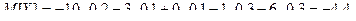

6.4. Пусть теперь 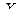- непрерывная случайная величина с плотностью распределения 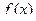. Чтобы найти математичес -кое ожидание функции 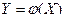, можно воспользоваться двумя способами:

а) сначала найти плотность распределения 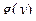данной функции и непосредственно применить формулу для вычисле -ния математического ожидания

;

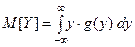б) если отыскание плотности 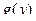вызывает затруднение, то математическое ожидание можно найти по формуле

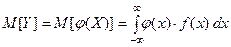Пример 6. Пусть задана плотность распределения случайной величины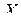

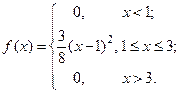
Найти математическое ожидание функции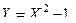

В этом примере математическое ожидание проще найти ис- пользуя способ б). Так как 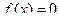вне промежутка 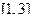, то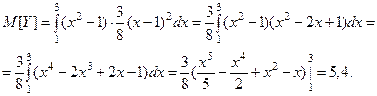

§ 7. ФУНКЦИЯ ДВУХ СЛУЧАЙНЫХ АРГУМЕНТОВ.

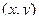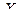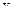Если каждой паре случайных величин и соответствует одно из возможных значений случайной величи- ны 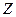, то 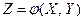называют функцией двух случайных агументов 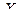и 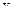. На практике наиболее часто встре- чается задача - найти закон распределения функции 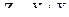по известным распределениям слагаемых. Напри- мер, если 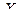- погрешность показаний некоторого измеритель- ного прибора (распределена, обычно, нормально) , а 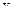- погрешность округления показаний этого прибора (распределе- на равномерно), то возникает задача - найти закон распреде -ления суммы погрешностей .

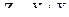7.1. Пусть 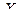и 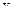- дискретные случайные величины,

которые заданы своими законами распределения. Тогда воз- можные значения случайной величины 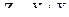- это все возможные значения сумм значени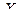й и 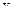, а вероятности соответствующих значений 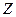находятся, как произведения со- ответствующих вероятностей значени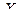й и 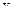, входящих в

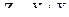и как суммы этих произведений, в случае, если одному значению суммы отвечают различные комбинации значени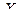й и .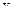

Пример 1. Пусть даны ряды распределения дискретных случайных величин 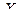и .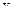

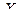
	-1	2	4
	0,2	0,5	0,3

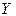
	2	4	5
	0,1	0,4	0,5

Тогда функция 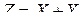принимает значения: 1, 3, 4, 6, 7, 8, 9. Вероятности этих значений находим , используя теоре -мы умножения и сложения вероятностей следующим образом:

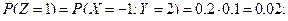
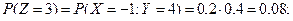
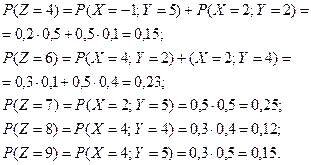
Получаем ряд распределения случайной величины :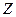

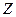
	1	3	4	6	7	8	9
	0,02	0,08	0,15	0,23	0,25	0,12	0,15

Сумма вероятностей, стоящих в нижней строке, равна 1, поэтому эта таблица в самом деле задаёт ряд распределения случайной величины .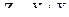

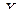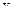7.2. Пусть теперь и - непрерывные случайные величины. Есл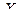и и 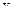- независимы, то зная плотности таспределения случайных величин 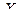и 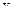- 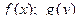, соответственно, плотность распределения случайной величины

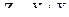можно найти по одной из следующих формул:

;

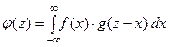или

В частности, если 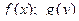принимают только положи- тельные значения на промежутке 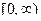, то выполняютя сле- дующие формулы:

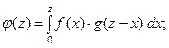
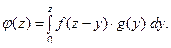
ПРИМЕР 2. Пусть независимые случайные величины 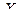и 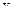заданы своими плотностями распределения:

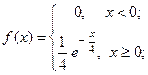
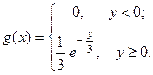
Найти закон распределения случайной величины .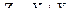

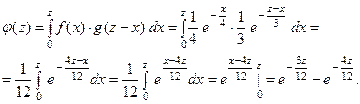
Таким образом,

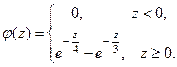
Легко проверить, что выполняется основное свойство плотнос -ти распределения, а именно,

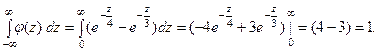
§ 8. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН

8.1 Законы распределения системы случайных величин.

Все случайные величины, которые рассматричались до сих пор, определялись одним числом (одним аргументом) - одно -мерные случайные величины. Но, кроме них, можем рассмот- реть величины, которые зависят от двух, трёх и более аргу –ментов, так называемые, многомерные случайные величины, которые можно рассматривать как системы одномерных слу -чайных величин. Через 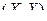- обозначают двумерную слу- чайную величину, а каждую из величин 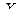и 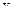- называют составляющей (компонентой).

Двумерную случайную величину называют дискретной, если её составляющие - дискретные случайные величины.

Непрерывной называют двумерную случайную величину, сос- тавляющие которой - непрерывные случайные величины.

Законом распределения дискретной двумерной случайной величинв называют таблицу вида:

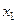
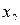
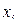
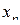
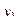
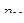
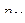
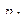
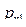
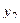
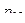
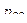
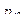
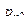
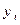
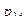
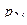
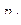
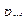
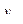
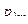
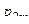
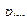
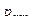
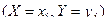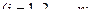
Так как события , 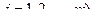образуют полную группу несовместных событий, то сумма всех вероятностей 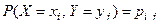, стоящих в таблице, равна единице.

Зная закон распределения двумерной случайной величины, можно найти закон распределения каждой составляющей:

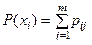(сумма вероятностей в столбце таблицы);

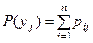(сумма вероятностей в строке таблицы).

Пример 1. Дан закон распределения двумерной случайной величины:

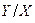
	2	3	5
-1	0,12	0,28	0,11
1	0,21	0,14	0,14

Составить законы распределения случайных величин 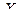и .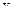

Случайная величина 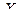имеет распределение:

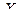
	2	3	5
	0,33	0,42	0,25

Для случайной величины 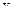получаем ряд:

⇐ Предыдущая 1 2 3 4 5 6 789 10 Следующая ⇒