Рис. 130 Построение выреза в цилиндре

Рис. 130 Построение выреза в цилиндре

Линии выреза, лежащие на боковой поверхности цилиндра, проецируются на окружность основания на П₁. Профильная их проекция строится по точкам измерения их глубин относительно плоскости симметрии цилиндра ф. Сквозные ребра 55' и 66' невидимы на П₁ и П₃

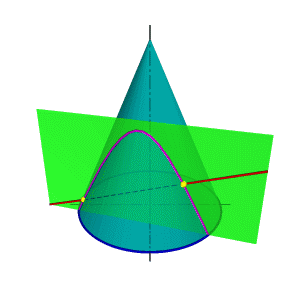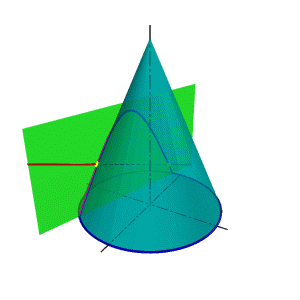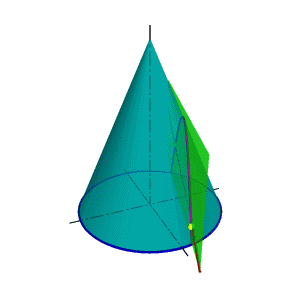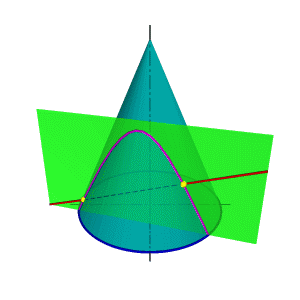
На рис. 130, б приведена задача построения выреза в конусе. Призматическое отверстие в конусе имеет три внутренние стенки, границами между которыми служат ребра АА', BE' и СС', которые перпендикулярны П2i. Правая стенка (АЕ) имеет форму трапеции, так как секущая плоскость этой стенки проходит через вершину S и пересекает конус по образующим SD и SD'. Части этих образующих между точками А (А') и В (В¹) дают контур правой стенки. Нижняя стенка (между ребрами ВВ' и СС') представляет собой часть круга, ограниченного параллельно h. Левая стенка (между ребрами АА' и СС') ограничена частью параболы, проекции которой определяются точками F (Р) на профильном меридиане конуса и промежуточными точками К (К') на вспомогательной параллели h'.

Профильный меридиан конуса «вырезан» на участке между точками Е (E')и F (F).

На рис. 130, в построены проекции сферы с вырезом. Призматическое отверстие имеет 4 внутренние стенки, границами между которыми служат ребра АА', ВВ', СС', DD', которые перпендикулярны П₂.

Каждая стенка представляет собой часть круга. Верхняя и нижняя параллельны П₁и проецируются на нее в виде части окружности с радиусами, которые определяются по параллелям h и h'.

Экватор вырезан между точками 1,5 и 2,6. Правая и левая стенки выреза параллельны П₃и проецируются на нее в виде частей круга с радиусами, которые определяются окружностями Р и Р'. Профильный меридиан вырезан между точками 3,7 и 4,8.

Приведенные примеры показывают, что, меняя положение секущих плоскостей, можно получить вырезы заданной формы.

пересечение прямой линии с поверхностью

При оценке взаимного расположения прямой линии и поверхности в качестве вспомогательных секущих поверхностей-посредников используется плоскость - метод вспомогательных секущих плоскостей.

Задача: Определить точки пересечения прямой линии с поверхностью конуса вращения и определить видимость прямой по отношению к конусу.

Для выбора вспомогательной секущей плоскости требуется знание линий образующихся в конических сечениях. Если в качестве вспомогательной секущей плоскости можно выбрать горизонтально проецирующую или фронтально проецирующую плоскости, то в сечении получатся соответственно гипербола (рис.111а) или эллипс (рис.111б). Построение кривых линий значительно усложняет задачу.




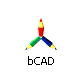
а) горизонтально проецирующая плоскость		б) фронтально проецирующая плоскость
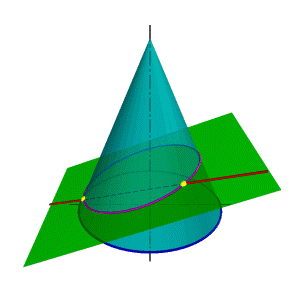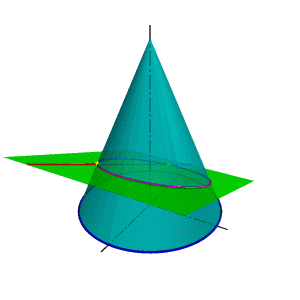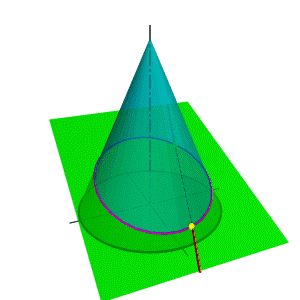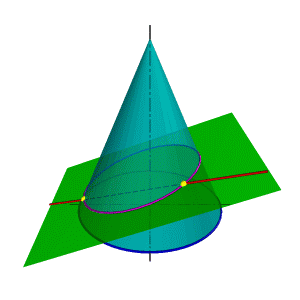
Рисунок 111. Пересечение прямой линии с конусом (вспомогательная секущая плоскость - проецирующая)

Поэтому в качестве вспомогательной секущей плоскости целесообразно выбрать такую плоскость, которая бы включала прямую l и пересекала конус по образующим (рис.112). Очевидно, что такая плоскость определяется прямой l и точкой S - вершиной конуса. Пусть основание конуса лежит в горизонтальной плоскости проекций, тогда линия пересечения вспомогательной секущей плоскости и горизонтальной плоскости проекций ВС пересекает основание конуса в точках D и F. Таким образом в сечении конуса вспомогательной секущей плоскостью получится треугольник DFS. Так как полученный треугольник и прямая l лежат в одной плоскости, точки их пересечения Ки М и есть точки пересечения прямой с конусом.





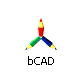
а) модель		б) эпюр
Рисунок 112. Пересечение прямой линии с конусом (вспомогательная секущая плоскость-плоскость общего

⇐ Предыдущая 5 6 7 8 9 10 11 12 1314