Рассмотренные винтовые поверхности, так же как и поверхности вращения, обладают свойством сдвигаемости, т. е. поверхность может перемешаться вдоль самой себя без каких-либо деформаций. Это свойство поверхности широко используется в технике при создан1. Ци

Рассмотренные винтовые поверхности, так же как и поверхности вращения, обладают свойством сдвигаемости, т. е. поверхность может перемешаться вдоль самой себя без каких-либо деформаций. Это свойство поверхности широко используется в технике при создан1. Циклические поверхности

Циклической поверхностью называется поверхность, образованная непрерывным каркасом круговых сечений.

На циклической поверхности расположено, по крайней мере, одно семейство круговых образующих (постоянного или переменного радиуса). Задание циклической поверхности должно однозначно определять положение плоскости каждой окружности, положение в плоскости и величину радиуса.

Циклическую поверхность можно задать плоскостью параллелизма, направляющей а и линией, которой принадлежат центры семейства окружностей Q (а, i, Г).

На рисунке показана поверхность Q (а, i, Г), где плоскости окружности циклической поверхности параллельны плоскости проекций П₁.

2. Трубчатые поверхности

Распространенные на практике разновидности циклических поверхностей - трубчатые поверхности переменного или постоянного радиуса.

ии винтовых пар (винт-гайка). На рис. 2.3.44 показан наклонный закрытый геликоид.

Пересечение поверхности с плоскостью. Тела с вырезами

При пересечении поверхности с плоскостью в сечении получают плоскую линию. Эту линию строят по отдельным точкам. В начале построения сперва выявляют и строят опорные точки, лежащие на контурных линиях поверхности, а также точки на ребрах и линиях основания поверхности. В тех случаях, когда проекция линии пересечения не полностью определяется этими точками, строят дополнительные, промежуточные точки, расположенные между опорными.

В данном разделе рассматриваются случаи пересечения поверхности плоскостями частного положения, так как в случае наличия секущей плоскости общего положения чертеж всегда можно преобразовать так, чтобы секущая плоскость стала проецирующей (см. рис. 129).

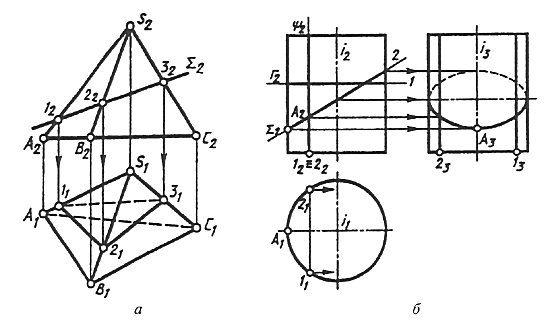
В случае пересечения гранной поверхности плоскостью получается плоская ломаная линия. Чтобы построить эту линию, достаточно определить точки пересечения плоскостью ребер и сторон основания, если имеет место пересечение основания, и соединить построенные точки с учетом их видимости (рис. 124, а).

⇐ Предыдущая 5 6 7 8 91011 12 13 14 Следующая ⇒