Конические поверхности

Конические поверхности

Коническая поверхность образуется движением прямой линии, скользящей по некоторой неподвижной замкнутой или незамкнутой кривой и проходящей во всех своих положениях через неподвижную точку (рис. 2.3.24).
Рис. 2.3.24

Неподвижная кривая m(m₁,m₂), по которой скользит образующая l(l₁,l₂), называется направляющей. Если направляющая линия является кривой второго порядка, то и коническая поверхность будет второго порядка. Неподвижная точка S(S₁,S₂), делящая поверхность на две бесконечные полы, называется вершиной. Множество прямолинейных образующих представляет собой непрерывный каркас конической поверхности. Через каждую точку поверхности проходит одна прямолинейная образующая (исключением является только вершина S, которая называется "особой точкой поверхности". Геометрическая часть определителя конической поверхности состоит из направляющей кривой m и вершины S.
Алгоритмическая часть определителя состоит из указания о том, что любая образующая поверхности может быть построена как прямая, проходящая через вершину S и пересекающая кривую m. Часть замкнутой конической поверхности, ограниченная вершиной и какой-либо плоскостью, пересекающей все ее образующие, называется конусом. Фигура сечения конической поверхности этой плоскостью называется основанием конуса. Сечение конической поверхности плоскостью, перпендикулярной ее оси, называется нормальным. Осью конической поверхности называется линия пересечения ее плоскостей симметрии. Следовательно, не все конические поверхности имеют ось, а только те, которые имеют не меньше двух плоскостей симметрии.
Конические поверхности, не имеющие оси (а следовательно, и нормального сечения), называются коническими поверхностями общего вида.

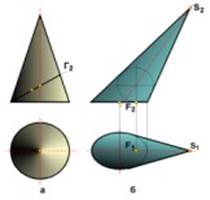Рис. 2.3.25

Конические поверхности, имеющие ось, в зависимости от вида нормального сечения бывают:
1) круговые - нормальное сечение круг (рис. 2.3.25);
2) эллиптические - нормальное сечение эллипс (рис. 2.3.26) и другие.
Если за основание конуса принимается фигура его нормального сечения, конус называют прямым, если иное сечение - наклонным. Прямой круговой конус изображен на рис. 2.3.25, а, наклонный круговой конус - на рис. 2.3.25, б. Основанием такого конуса может быть только эллипс (см. раздел 4), ось его не проходит через центр основания.
Прямой эллиптический конус показан на рис. 2.3.26, а. Эллиптический конус (так же как и эллиптический цилиндр) имеет две системы круговых сечений. Построение круговых сечений поверхностей второго порядка рассматривается в разделе 4.3.

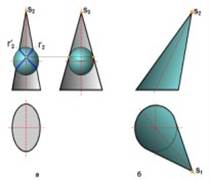Рис. 2.3.26

Если принять одно из них за основание конуса, получим наклонный эллиптический конус с круговым основанием (рис. 2.3.26, б). Ось наклонного конуса не проходит через центр основания. Заметим, что у всех развертывающихся линейчатых поверхностей две смежные образующие либо пересекаются (торс, коническая поверхность), либо параллельны (цилиндрическая поверхность).

Линейчатые поверхности с плоскостью параллелизма

Линейчатые поверхности находят широкое применение при строительстве сооружений, а также при конструировании оболочек перекрытий промышленных и общественных зданий, в кораблестроении, авиационной промышленности и в автомобилестроении.

Линейчатой поверхностью с плоскостью параллелизма называется поверхность, образованная перемещением прямолинейной образующей по двум направляющим. При этом образующая в любом положении сохраняет параллельность некоторой заданной плоскости, которая называется плоскостью параллелизма.

В зависимости от формы и взаимного расположения направляющих различают следующие виды линейчатых поверхностей:

· · Цилиндроид – прямолинейная образующая движется по первой и второй направляющим, являющимися кривыми линиями, параллельно заданной плоскости.

· · Коноид – прямолинейная образующая движется по первой и второй направляющим, одна из которых прямая линия, а вторая – кривая линия, параллельно заданной плоскости.

· · Косая плоскость (гиперболический параболоид) – прямолинейная образующая движется по первой и второй направляющим, являющимися прямыми линиями, параллельно заданной плоскости.

Репер линейчатой поверхности с плоскостью параллелизма состоит из двух линий - направляющих и плоскости параллелизма. При моделировании линейчатых поверхностей на эпюре Монжа в качестве плоскости параллелизма обычно используют проецирующую плоскость или одну из плоскостей проекций.

Все линейчатые поверхности могут иметь каркас в виде прямолинейных образующих. При этом построение образующих, принадлежащих заданной поверхности, удобно начинать на той плоскости проекций, где плоскость параллелизма вырождается в прямую линию.

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒