Косая плоскость

Косая плоскость

Косой плоскостью называется поверхность, образованная движением прямой линии, скользящей по двум скрещивающимся прямым и остающейся во всех своих положениях параллельной некоторой плоскости параллелизма.
Косая плоскость, направляющими которой являются скрещивающиеся прямые m(m₁,m₂) и n(n₁,n₂), а плоскостью параллелизма - плоскость П₁, показанная на рис. 2.3.35.
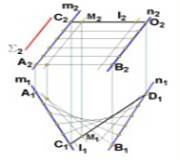Рис. 2.3.35

Ту же самую поверхность можно получить, если за направляющие прямые принять любую пару образующих, например АВ(А₁В₁, А₂В₂) и СD(С₁D₁, С₂D₂), за образующую прямую - одну из направляющих (m или n) и за плоскость параллелизма - плоскость 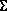( 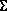₂), параллельную прямым m и n. Таким образом, косая плоскость имеет два семейства прямолинейных образующих и две плоскости параллелизма. Образующие одного семейства - скрещивающиеся прямые, каждая образующая одного семейства пересекает все образующие второго. Поэтому через каждую точку поверхности проходят две прямолинейные образующие разных семейств.
Косую плоскость называют также гиперболическим параболоидом, так как при пересечении ее соответствующими плоскостями в сечении можно получить параболы и гиперболы. Геометрическая часть определителя косой плоскости состоит из направляющих прямых и плоскости параллелизма: Алгоритмическая часть определителя состоит из указания о том, что любая образующая поверхности может быть построена как прямая, пересекающая направляющие прямые и параллельная плоскости параллелизма.

Рис. 2.3.36 (анимация)

Анимация (рис. 2.3.36) поясняет формирование косой плоскости, как поверхности с плоскостью параллелизма. Образующие косой плоскости формируются вспомогательной плоскостью, перемещающейся параллельно плоскости параллелизма. Аанимационный слайд 2.3.37 демонстрирует одно из свойств косой плоскости - наличие второй плоскости параллелизма.
Видно, что для косой плоскости, построенной в предыдущем примере, существует второе семейство образующих, которые могут быть получены перемещением другой вспомогательной плоскости со своей, второй плоскостью параллелизма.
Рис. 2.3.37

На рис. 2.3.38 поясняется существование семейства параболических сечений. Косая плоскость может быть получена как поверхность Каталана путем плоскопараллельного перемещения одной из парабол, как образующей, по второй параболе, как направляющей. Результат этого кинематического варианта формирования косой плоскости показан на рис. 2.3.39, где представлена та же косая плоскость, что и в предыдущих примерах, но с другим каркасом.

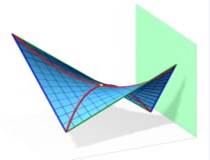Рис. 2.3.38 Рис. 2.3.39

На рисунке так же показан пример гиперболического сечения рассматриваемой поверхности и его вырожденный случай - две прямые, проходящие через "седловую" точку.

⇐ Предыдущая 3 4 5 6 789 10 11 12 Следующая ⇒