Цилиндрические поверхности

Цилиндрические поверхности

Цилиндрическая поверхность образуется движением прямой линии, скользящей по некоторой неподвижной замкнутой или незамкнутой кривой и остающейся параллельной своему исходному положению (рис. 2.3.21). Множество прямолинейных образующих представляет собой непрерывный каркас цилиндрической поверхности. Через каждую точку поверхности проходит одна прямолинейная образующая.
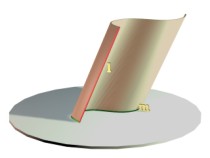Рис. 2.3.21

Неподвижная кривая m(m₁ m₂), по которой скользит образующая l(l₁l₂), называется направляющей. Если направляющая линия является кривой второго порядка, то и цилиндрическая поверхность будет второго порядка. Геометрическая часть определителя цилиндрической поверхности состоит из направляющей линии m и исходного положения образующей l (рис. 2.3.21).
Алгоритмическая часть определителя состоит из указания о том, что любая образующая поверхности может быть построена как прямая, пересекающая кривую m и параллельная прямой l. Цилиндрическая поверхность является бесконечной в направлении своих образуюших. Часть замкнутой цилиндрической поверхности, заключенная между двумя плоскими параллельными сечениями, называется цилиндром, а фигуры сечения - его основаниями (рис. 2.3.22, 2.3.23). Сечение цилиндрической поверхности плоскостью, перпендикулярной ее образующим, называется нормальным. В зависимости от формы нормального сечения цилиндры бывают:
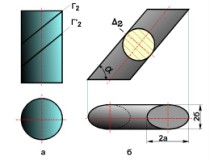Рис. 2.3.22

1) круговые - нормальное сечение круг (рис. 2.3.22);
2) эллиптические - нормальное сечение эллипс (рис. 2.3.23);
3) параболические - нормальное сечение парабола;
4) гиперболические - нормальное сечение гипербола;
5) общего вида - нормальное сечение кривая случайного вида (рис. 2.3.20). Если за основание цилиндра принимается его нормальное сечение, цилиндр называют прямым(2.3.22, а).
Если за основание цилиндра принимается одно из косыхсечений, цилиндр называют наклонным (рис. 2.3.22, б, 2.3.23, б, в).
Наклонные сечения прямого кругового цилиндра являются эллипсами (сечения плоскостям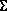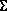и ( ₂) и 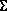'( ' 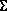₂) на рис. 2.3.22, а). На рис. 2.3.22, б изображен наклонный цилиндр, основаниями которого являются косые сечения (эллипсы).
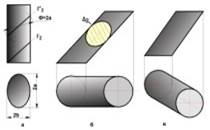Рис. 2.3.23

Наклонные сечения прямого эллиптического цилиндра в общем случае - эллипсы. Однако его всегда можно пересечь плоскостью, наклонной к его образующим, таким образом, что в сечении получится круг. Эллиптический цилиндр имеет две системы круговых сечений (построение их рассмотрено в гл. 4). На рис. 2.3.23, а показаны плоскости Г(Г₂) и Г'(Г'₂), пересекающие эллиптический цилиндр по окружностям. На рис. 2.3.23, б, в выполнены чертежи наклонных эллиптических цилиндров, основаниями которых являются их круговые сечения.

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒