Уравнение сферы.. Взаимное расположение сферы и плоскости

Уравнение сферы.

Выведем уравнение сферы (см. начало п. 53) радиуса R с центром С (х₀; у₀; z₀) (рис. 159).

Расстояние от произвольной точки М (х; у; z) до точки С вычисляется по формуле MC = 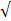(x- x₀)² +(у-у₀)² + (z-z₀)².

Если точка М лежит на данной сфере, то МС = R, или МС² = R², т. е. координаты точки М удовлетворяют уравнению

(х-х₀)²+(у-у₀)²+(z-z₀)² =R². (1)

Если же точка М (х; у; z) не лежит на данной сфере, то МС² 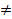R², т. е. координаты точки М не удовлетворяют уравнению (1). Следовательно, в прямоугольной системе координат уравнение сферы радиуса R с центром С (x₀; у₀; z₀) имеет вид(х- x₀)² +(у-у₀)² +(z-z₀)² =R².

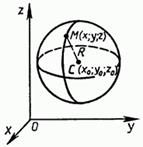
Рис .159

Взаимное расположение сферы и плоскости

Исследуем взаимное расположение сферы и плоскости в зависимости от соотношения между радиусом сферы и расстоянием от ее центра до плоскости.

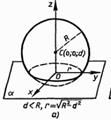
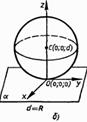
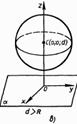
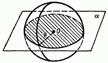
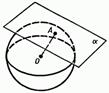
Обозначим радиус сферы буквой R, а расстояние от ее центра до плоскости α — буквой d. Введем систему координат так, как показано на рис. 160: плоскость Оху совпадает с плоскостью α, а центр С сферы лежит на положительной полуоси Oz. В этой системе координат точка С имеет координаты (0; 0; d), поэтому сфера имеет уравнение х² + у² + (z – d)² = R². Плоскость α совпадает с координатной плоскостью Оху, и поэтому ее уравнение имеет вид z = 0 (объясните почему).

Если координаты какой-нибудь точки М (х; у; z) удовлетворяют обоим уравнениям, то точка М лежит как в плоскости а, так и на сфере, т. е. является общей точкой плоскости и сферы.

Если же система этих двух уравнений не имеет решений, то сфера и плоскость не имеют общих точек. Таким образом, вопрос о взаимном расположении сферы и плоскости сводится к исследованию системы уравнений 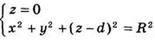Подставив z = 0 во второе уравнение, получим х² + у² = R²- d² (2)

Возможны три случая.

⇐ Предыдущая 1 2 3 4 5 678 9 Следующая ⇒