Хелпикс

Главная

Контакты

Случайная статья



Рис .148 Рис .149 Рис .150 Рис .151 Рис .152

⇐ ПредыдущаяСтр 5 из 9Следующая ⇒


  Рис .148                        Рис .149                                     Рис .150                      Рис .151              Рис .152

Площадь поверхности конуса

Боковую поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на плоскость, разрезав ее по одной из образующих (рис. 153, а, б). Разверткой боковой поверхности конуса является круговой сектор (см. рис. 153, б), радиус которого равен образующей конуса, а длина дуги сектора равна длине окружности основания конуса.

За площадь боковой поверхности конуса принимается площадь ее развертки.

Выразим площадь S6oк боковой поверхности конуса через его образующую l и радиус основания г. Площадь кругового сектора — развертки боковой поверхности конуса (см. рис. 153, б) - равна 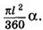где α –градусная мера дуги АВА, поэтому  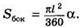 (1)

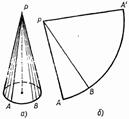
Рис .153

Выразим α через l и г. Так как длина дуги АВА' равна 2πг (длине окружности основания конуса),то 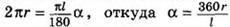. Подставив это выражение в формулу (1), получим

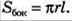
Таким образом, площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Для вычисления площади Sкон полной поверхности конуса получается формула

 

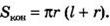
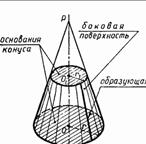
Усеченный конус
Возьмем произвольный конус и проведем секущую плоскость, перпендикулярную к его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей (верхняя на рис. 154) представляет собой конус, а другая называется усеченным конусом.Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усеченного конуса, а отрезок, соединяющий их центры,— высотой усеченного конуса. Часть конической поверхности, ограничивающая усеченный конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, заключенные между основаниями, называются образующими усеченного конуса. Все образующие усеченного конуса равны друг другу (докажите это самостоятельно).   Усеченный конус может быть получен вращением прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к основаниям. На рисунке 155 изображен усеченный конус, полученный вращением прямоугольной трапеции ABCD вокруг стороны CD, перпендикулярной к основаниям AD и ВС. При этом боковая поверхность образуется вращением боковой стороны АВ, а основания усеченного конуса — вращением оснований СВ и DA трапеции.


⇐ Предыдущая123456789Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.