Лекция по геометрии «Цилиндр, конус и шар». Индивидуальные задания

Лекция по геометрии «Цилиндр, конус и шар». Индивидуальные задания

Понятие цилиндра.

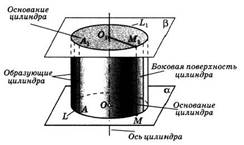
Рассмотрим произвольную плоскость α и окружность L с центром О радиуса г, лежащую в этой плоскости. Через каждую точку окружности L проведем прямую, перпендикулярную к плоскости α. Поверхность, образованная этими прямыми, называется цилиндрической поверхностью, а сами прямые — образующими цилиндрической поверхности. Прямая, проходящая через точку О перпендикулярно к плоскости α, называется осью цилиндрической поверхности. Поскольку все образующие и ось перпендикулярны к плоскости α, то они параллельны друг другу (см. п. 16).

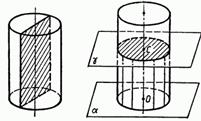
Рассмотрим теперь плоскость β, параллельную плоскости α (рис. 142). Отрезки образующих, заключенные между плоскостями α и β, параллельны и равны друг другу (см. п. 11). По построению концы этих отрезков, расположенные в плоскости α, заполняют окружность L. Концы же, расположенные в плоскости β, заполняют окружность L₁ с центром О₁ радиусаг, где O₁ — точка пересечения плоскости β с осью цилиндрической поверхности.

Справедливость этого утверждения следует из того, что множество концов образующих, лежащих в плоскости β, получается из окружности L параллельным переносом на вектор 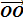₁. Параллельный перенос является движением и, значит, наложением, а при наложении любая фигура переходит в равную ей фигуру. Следовательно, при параллельном переносе на вектор 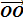₁ окружность L перейдет в равную ей окружность L₁ радиуса г с центром в точке О₁

Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и L₁ называется цилиндром (см. рис. 142). Круги называются основаниями цилиндра, отрезки образующих, заключенные между основаниями, — образующими цилиндра, а образованная ими часть цилиндрической поверхности — боковой поверхностью цилиндра. Ось цилиндрической поверхности называется осью цилиндра.

Как уже отмечалось, все образующие цилиндра параллельны и равны друг другу. Длина образующей называется высотой цилиндра, а радиус основания — радиусом цилиндра.

12 3 4 5 6 7 8 9 Следующая ⇒