Сфера и шар

Рис .154

Рис .155

Можно доказать, что площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую, т. е.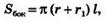

где г и г₁— радиусы оснований, l — образующая усеченного конуса.

1. Высота конуса равна 15 см, а радиус основания равен 8 см. Найдите образующую конуса.

2. Образующая конуса, равная 12 см, наклонена к плоскости основания под углом α. Найдите площадь основания конуса, если: а) α = 30°; б)α = 45°; в) α = 60°.

3. Осевое сечение конуса — прямоугольный треугольник. Найдите площадь этого сечения, если радиус основания конуса равен 5 см.

4. Найдите высоту конуса, если площадь его осевого сечения равна 6 дм², а площадь основания равна 8 дм².

5.Высота конуса равна 10 см. Найдите площадь сечения, проходящего через вершину конуса и хорду основания, стягивающую дугу в 60°, если плоскость сечения образует с плоскостью основания конуса угол: а) 30°; б) 45°; в) 60°.

6.Прямоугольный треугольник с катетами 6 см и 8 см вращается вокруг меньшего катета. Вычислите площади боковой и полной поверхностей образованного при этом вращении конуса.

Сфера и шар

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки (рис. 157).

Данная точка называется центром сферы (точка О на рис. 150), а данное расстояние — радиусом сферы. Радиус сферы часто обозначают буквой R.

Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы. Очевидно, диаметр сферы равен 2R. Отметим, что сфера может быть получена вращением полуокружности вокруг ее диаметра (рис. 151).

Тело, ограниченное сферой, называется шаром.Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара. Очевидно, шар радиуса R с центром О содержит все точки пространства, которые расположены от точки О на расстоянии, не превышающем R (включая и точку О), и не содержит других точек.

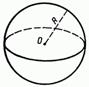Рис .157

Рис .158

⇐ Предыдущая 1 2 3 4 567 8 9 Следующая ⇒