Хелпикс

Главная

Контакты

Случайная статья



Задача №2. Задача №135

⇐ ПредыдущаяСтр 7 из 7


Задача №2

Определить избыточное давление воздуха в напорном баке по показанию ртутного манометра, составленного из двух U-образных трубок. Отметки уровней даны в метрах.

 

Дано:

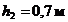
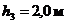
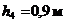
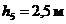
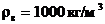
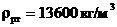
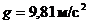
Решение:

Рис. 1.

Найти:

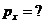
Согласно основному уравнению гидростатики, избыточное давление в точке А

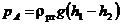,                                            (1)

где 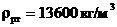 – плотность ртути.

Избыточное давление в точке В

,

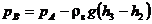или, с учетом формулы (1),

,                              (2)

где 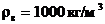 – плотность воды.

Избыточное давление в точке С

,

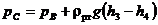или, с учетом формулы (2),

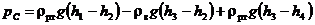.                    (3)

С другой стороны, основному уравнению гидростатики избыточное давление в точке С

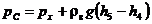.                                       (4)

Приравнивая правые части выражений (3) и (4), получим

,

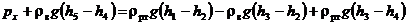откуда избыточное давление воздуха в напорном баке

.

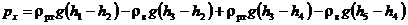Проведем вычисления

.

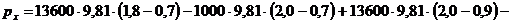
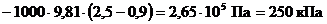Ответ: 250 кПа.

Задача №135

Вода при температуре 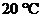 перетекает из напорного бака в резервуар по трубе диаметром  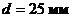и длиной 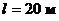. Избыточное давление воздуха в напорном баке 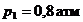, уровни воды Н1= 1, 5 м, Н2= 2, 5 м. Определить расход Q методом последовательных приближений или путем построения характеристики трубопровода. Труба гладкая – местными сопротивлениями пренебречь.

 

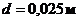
Дано: 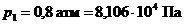Н1= 1, 5 м Н2= 2, 5 м

Решение:

Рис. 1.

Найти:

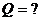
При температуре Т = 20 °С плотность воды 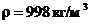, коэффициент кинематической вязкости  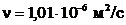[1].

Выберем сечения 1–1 по свободной поверхности жидкости в баке, сечение 2–2 – по свободной поверхности жидкости в резервуаре, как показано на рис. 1. Плоскость сравнения совместим с сечением 1–1.

Составим уравнение Бернулли для сечений 1–1 и 2–2

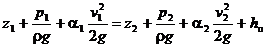.                                  (1)

В рассматриваемом случае , .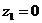

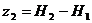Так как уровни жидкости в баке и резервуаре поддерживаются постоянными, то .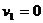

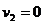Так как резервуар является открытым, то избыточное давление  .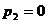

Подставив все значения в уравнение Бернулли (1), получим

,

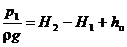По условию задачи потерями в местных сопротивлениях можно пренебречь, тогда потери напора будут обусловлены только потерями на трение по длине трубы, т. е.

.

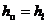Следовательно,

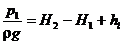.                                               (2)

Согласно формуле Дарси потери напора на трение по длине l

,

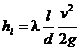где 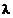 – коэффициент сопротивления трения, v – средняя скорость воды в трубопроводе.

Выполним решение уравнения (2) методом последовательных приближений.

Первое приближение.

В первом приближении примем, что режим течения воды в трубопроводе турбулентный, тогда, учитывая, что по условию задачи труба является гладкой, коэффициент 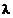 можно определить по формуле Блазиуса

,

где 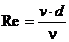 – число Рейнольдса.

Тогда потери напора на трение по длине

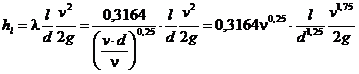.           (3)

Подставляя выражение (3) в формулу (2), получим

,

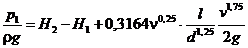откуда средняя скорость воды в трубопроводе

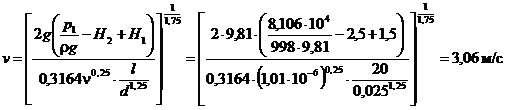
Определим число Рейнольдса

.

Так как 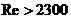, то режим течения в трубе турбулентный, следовательно, наше предположение при выборе формулы для  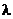было верным и уточнять значение скорости не требуется.

Определим расход воды

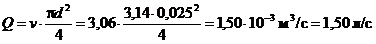
Ответ: .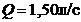

 

 

Литература.

1. Примеры расчетов по гидравлике: учеб. пособие для строит. спец. вузов/ А. Д. Альтшуль и др. – М.: Стройиздат, 1977. – 255 с.

2. Машиностроительная гидравлика. Примеры расчетов. / В. В. Вакина и др. –Киев: Вища шк., 1986. – 208 с.

3.  Гидравлика, гидромашины и гидроприводы // Т. М. Башта, С. С. Руднев, Б. Б. Некрасов и др. М.: Машиностроение, 1982. 423 с.

 

 


⇐ Предыдущая1234567
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.