- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача № 61.. Задача № 119.
Задача № 61.
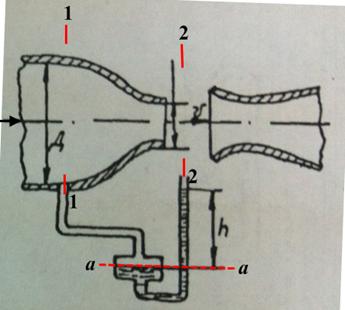
Аэродинамическая труба имеет открытую рабочую часть диаметром 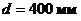 . Спиртовой чашечный манометр присоединен к широкой части трубы, диаметр которой
. Спиртовой чашечный манометр присоединен к широкой части трубы, диаметр которой 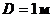 . Определить скорость потока воздуха в рабочей части, если показание манометра
. Определить скорость потока воздуха в рабочей части, если показание манометра 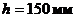 (
( 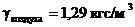 ,
, 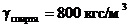 ).
).
Дано:
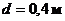
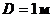
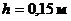
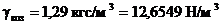


| Решение:
Рис. 1. |
Найти:
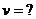
|
Запишем уравнение Бернулли для сечений 1–1 и 2–2 без учета потерь напора, принимая за плоскость сравнения ось трубы:
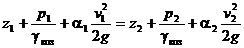 , (1)
, (1)
где 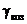 – удельный вес воздуха.
– удельный вес воздуха.
В рассматриваемом случае 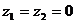 ,
, 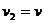 , где
, где 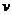 – скорость потока воздуха в рабочей части.
– скорость потока воздуха в рабочей части.
В предположении, что режим течения воздуха – турбулентный, принимаем значение 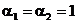 .
.
Следовательно, уравнение Бернулли (1) примет вид
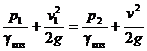 ,
,
откуда
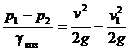 . (2)
. (2)
Запишем условие равновесия жидкости в спиртовом чашечном манометре относительно плоскости а – а
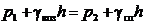 ,
,
где  – удельный вес спирта.
– удельный вес спирта.
Тогда
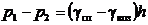 . (3)
. (3)
Для определения скорости выразим одну скорость через другую, используя уравнение расхода и пренебрегая изменением плотности воздуха,
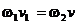 .
.
Поскольку площади 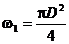 и
и 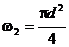 , получим
, получим
 ,
,
откуда
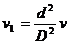 . (4)
. (4)
Подставляя выражение (3) и (4) в формулу (2), получим
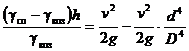 ,
,
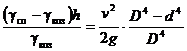 ,
,
откуда скорость воздуха в рабочей части трубы
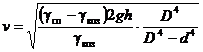 .
.
Проведем вычисления
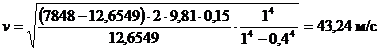 .
.
Ответ:  .
.
Задача № 119.
В пластинчатом радиаторе системы водяного охлаждения авиадвигателя вода течет в зазорах между стенками, которые снаружи обдуваются воздухом. Для лучшей теплопередачи от воды к воздуху течение воды должно быть турбулентным. определить минимальную допустимую скорость движения воды в зазоре из условия получения турбулентного режима. Величина зазора h = 2 мм, температура воды 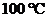 . Критическое число Рейнольдса принять таким же, как и для круглой трубы, но выразить через гидравлический радиус.
. Критическое число Рейнольдса принять таким же, как и для круглой трубы, но выразить через гидравлический радиус.
Дано:
h = Rг = 2 мм = 0, 002 м
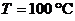 n = 0, 29 · 10–6 м2/с
n = 0, 29 · 10–6 м2/с
|
Найти:
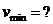
|
Решение:
Примем критическое число Рейнольдса таким же, как и для круглой трубы
 ,
,
где  – критическая скорость движения воды в трубе,
– критическая скорость движения воды в трубе, 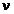 – коэффициент кинематической вязкости воды.
– коэффициент кинематической вязкости воды.
Следовательно, критическая скорость
 .
.
При температуре 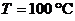 коэффициент кинематической вязкости воды
коэффициент кинематической вязкости воды
n = 0, 29 · 10–6 м2/с.
Вычислим 
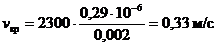 .
.
Таким образом, минимальная скорость воды в канале должна быть 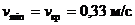 .
.
Ответ: 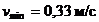 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|