Хелпикс

Главная

Контакты

Случайная статья



Задача № 129

⇐ ПредыдущаяСтр 5 из 7Следующая ⇒


На рисунке показана схема всасывающего участка маслопровода на самолете. Определить абсолютное давление масла перед входом в насос при высоте полета Н = 8 км (атмосферное давление 266, 8 мм. рт. ст). Расход масла Q = 1, 25 л/с, диаметр трубы 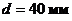, длина 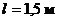, температура масла 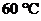. Коэффициент сопротивления крана 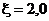; 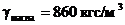. Высота h = 1 м. Давление в баке равно атмосферному.

 

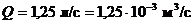
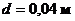
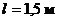
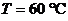
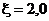
Дано: Н = 8 км 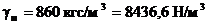h = 1 м

Решение:

Рис. 1.

Найти:

 

Выберем сечения 1–1 по свободной поверхности жидкости в баке, сечение 2–2 – на входе в насос, как показано на рис. 1. Плоскость сравнения совместим с осью горизонтальной трубы.

Составим уравнение Бернулли для сечений 1–1 и 2–2

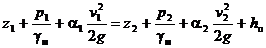.                                  (1)

В рассматриваемом случае 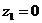, , 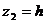,  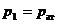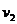– средняя скорость жидкости в трубопроводе.

Так сечение 1–1 выбрано по свободной поверхности жидкости в баке, то скоростной напор 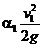  пренебрежимо мал по сравнению с остальными членами уравнения (1), поэтому им можно пренебречь, т. е. полагаем .

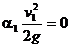Средняя скорость жидкости в сечении 2–2

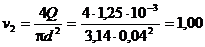 м/с.

Так как вид масла не задан, то коэффициент кинематической вязкости масла при температуре 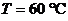 примем ориентировочно .

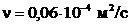Определим число Рейнольдса

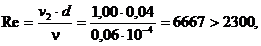
следовательно, режим течения турбулентный и коэффициент Кориолиса .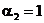

Подставив все значения в уравнение Бернулли (1), получим

,

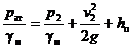откуда абсолютное давление на входе в насос

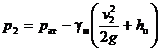 .                                         (2)

Потери напора 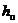 складываются из потерь на трение по длине трубопровода  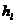и местных потерь 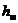, т. е.

.

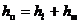Местные потери 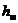 определим по формуле Вейсбаха

,

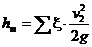где 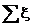 – суммарный коэффициент местных сопротивлений.

В рассматриваемом случае местные сопротивления (рис. 1):

– вход из бака в трубопровод с коэффициентом сопротивления ;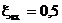

– кран с коэффициентом сопротивления .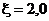

Таким образом,

.

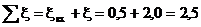Вычислим потери напора в местных сопротивлениях

.

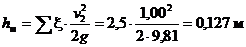Потери напора на трение по длине l определим по формуле Дарси

,

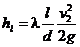где 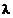 – коэффициент сопротивления трения.

Так как режим течения – турбулентный, то коэффициент 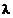 определяем по формуле Блазиуса

.

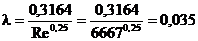Вычислим потери напора на трение по длине l

.

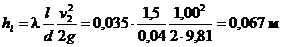Суммарные потери напора

.

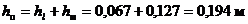По формуле (2) вычислим абсолютное давление на входе в насос

.

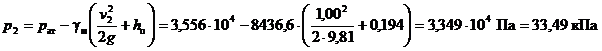Ответ: .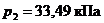


⇐ Предыдущая1234567Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.