3. Дискретті хабарламаның өнімділік қоры

⇐ ПредыдущаяСтр 25 из 40Следующая ⇒

3. Дискретті хабарламаның ө німділік қ оры

Тақ ырып 9. Ү здіксіз хабарлама кө зі мен ү здіксіз байланыс арналарының ақ параттық сипаттамалары.

Дә ріс мақ саты:

1. Ү здіксіз хабарлама кө зінің ақ параттық сипаттамаларын зерттеп тану.

2. Ү здіксіз байланыс арналарының ақ параттық сипаттамалары

Сұ рақ тар:

1. Эпсилон тү сінігі.

2. Ү здіксіз хабарлама кө зі мен ақ параттық сипаттамалары қ андай?

3. Ү здіксіз байланыс арналарының ақ параттық сипаттамалары қ андай болады?

1. Ү здіксіз хабарлама кө зі ақ параттық сипаттамалары

Эпсилон- ү здіксіз хабарлама кө зінің ө німділігі. Нақ ты тү рде Ү здіксіз хабарлама 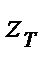(t) кез келген процестің Т уақ ыт аралығ ында қ андай да бір орындауын білдіреді. Ү здіксіз хабарлама кө зін орындау ансамблімен сипатталады. Ең ө німді модель ол эргодикалық кездейсоқ процесс тү ріндегі ү здіксіз хабарлама болды.

Ү здіксіз хабарлама кө зінің ө німділігін анық тау ү шін ε –кездейсоқ шаманың энтропиясы анық талғ ан § 3. 7 қ орытындысы мен жолын қ олданады.

Берілген ε ық тималдылық пен кез келген 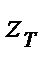(t) орындау ү шін бірлік уақ ытта қ ұ рылатын, минималды ақ парат санымен ү здіксіз хабарлама кө зі Η ε (z) ε -ө німділігімен тү сіндіріледі.

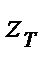(t) uT(t)-ның жү зеге асырылуы арқ ылы қ айталанады деп есептейік. Бақ ыланып отыратын жү зеге асыруларды шектеулі немесе жеткілікті жалпақ спектрлі F [28, 8] сигнал деп қ арастыруғ а болады. Жеткілікті мө лшердегі ү лкен ұ зақ тық та Т 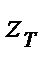(t) немесе uT(t) ретінде де N-шамалы (N = 2FT) векторы ретінде жә не санау болып табылатын ( 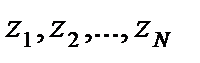) жә не ( 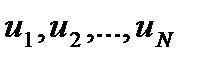) координаттары тү рінде де кө рсетілуі мү мкін. { 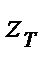(t)} хабарламасының ансамблі жә не {uT(t)} қ айталанушы сигналдарды Ζ 1, Z2, .., ZN и U1, U2, .., UN кездейсоқ шамаларына сә йкес келетін N-шамалық кездейсоқ Ζ жә не U векторларын сипаттайды. Ансамбльдің ә рқ айсысының статистикалық сипаттамасы N-шамалық ық тималдық ты тарату тығ ыздығ ымен ρ (Ζ ) = ρ ( 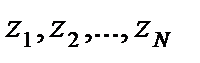) жә не p(U) = p( 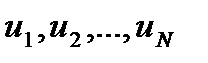) беріледі. Ансамбльдер арасындағ ы байланыс pu(Z)= ρ ( 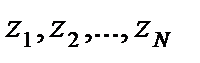/ 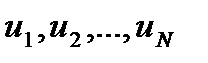) жә не pz(U) = p( 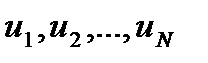/ 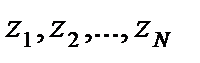) ық тималдық ты тарату шартты тығ ыздығ ы жә не ық тималдық ты таратудың сә йкес тығ ыздығ ымен p(Z, U) = p( 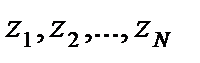; 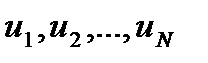) кө рсетіледі.

(4. 20) формуласын кең ейту арқ ылы N-шамалық Ζ жә не U кездейсоқ векторлары ақ параттық саны ү шін олардың біріншісі екіншісіне салыстырмалы тү рде келесі формуланы аламыз:

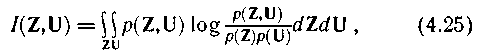
Мұ нда интеграл N-шамалы болып саналады.

Туралық тың 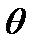орташашаршылық критерийін (Z, U), қ олданамыз, жә не оны келесідей тү рде қ арастырамыз:

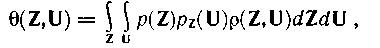
Мұ нда, p(Z, U)ZU ара қ ашық тық шаршысын l(Z, U) N-шамалы евклидтық кең істікте кө рсетіледі.

Бір дискреттік сигналдарды ZT(t) жә не UT(t) есептеуге ө туші ақ параттардың саны келесідей жолмен анық талады:

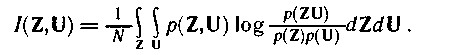
ε -пропорционал ү здіксіз хабарламалар кө здері Нε (Z) сай анық тама ү шін келесідей жазамыз:

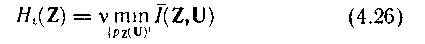
Шартты орындағ ан жағ дайда:

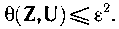
ν шамасы есептеу кө здерінің қ ұ рылу жылдамдығ ын сипаттайды (ν = =2F).

Мысал 4. 5. ε -ө німділік кө зін ν 1 жылдамдығ ымен жасалғ ан ө зара байланыссыз σ 2дисперсиясымен тұ рақ ты орташа кездейсоқ сигналдарды есептеулерді анық тау.

(3. 65) алынғ ан орташа таратылғ ан кездейсоқ шамасы ε -энтропиясын қ олдана отырып, табамыз:

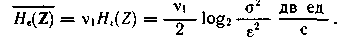
Кез келген zT(t) хабарламасын берілген туралық пен қ айта есептеу мү мкіндігі геометриялық тү сінікті береді. Эргодикалық процестердің жү зеге асырылуы жеткілікті ұ зақ уақ ытта типтік болып табылады жә не бірдей орташа қ уаттылық қ а ие болады, N-шамалық кең істіктегі векторларғ а ү зіліссіз кө п нү ктелерден тұ ратын хабарламалар тең ө шірілген координаттар басынан (гиперсфера) қ ұ ралғ ан.

Қ айталанатын сигналдардың соң ғ ы кө пшілігі UT(t) қ иылыспайтын тү зу сфералық N-бұ рыштардың орталығ ында (ε -аймағ ы) гиперсфера аралық сыз дамиды. ε -аймағ ының ө лшемі хабарламаны берілген қ айталау туралығ ы анық талғ ан. Егер тү пнұ сқ асы болып z*T(t) хабарламасы жү зеге асырылса, ε -аймағ ы тү суі керек вектордың соң ы u*T(t) сигналына тү ссе, онда u*T(t) сигналы қ айталанады.

Кө рсете кететін жайт, қ айталанудың берілген туралығ ы, тек хабарламаның жеткілікті ү лкен ұ зақ тығ ында ғ ана, бірлікке жақ ын ық тималдық пен жетеді, ү зіліссіз жү зеге асырылулардың жү йелілігінде есептеулерді елемеуге де болады. Берілген қ ате жіберулерді Т хабарламаның шектеулі ұ зақ тығ ында азайтуда N есептеулерінің санын ұ лғ айту керек. N→ ∞ шегінде ү зіліссіз жү зеге асырылуларды алуғ а болады.

ε – ө німділік кө зін есептен шығ аруда жә не хабарламларды қ айталау мү мкіндігін берілген туралық пен геометриялық тү сіндіруде негізінде ешнә рсе ө згермейді. Тек қ ана, N-шамалы евклидово хабарламалар кең істігі гильберттік болады жә не екі сигналдың жақ ындық шамасы осы кең істік ара қ ашық тығ ындай болуы керек.

⇐ Предыдущая 20 21 22 23 242526 27 28 29 Следующая ⇒