
- Р Р‡.МессенРТвЂВВВВВВжер
- ВКонтакте
- РћРТвЂВВВВВВнокласснРСвЂВВВВВВРєРСвЂВВВВВВ
- Telegram
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВВВВВРЎР‚
- LiveJournal
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тақырып 8. Дискретті хабарлама көздерінің моделі. Артықтық. Өнімділігі.
Дә ріс мақ саты: Дискретті хабарлама кө здерінің моделін зерттеу
Сұ рақ тар:
1. Дискретті хабарлама кө здерінің моделі
2. Эргодикалық жү йелілік белгілердің қ ұ рылысы
3. Дискретті хабарлама кө здерінің ө німділігі
Дискретті хабарлама кө здерінің моделі. Бұ рын сө з тек, бір жағ дайдағ ы ғ ана хабарлама кө зіне келетін орташа белгісіз жә не орташа кө лемді ақ парат туралы болатын. Бұ л дерек кө здерді жү зеге асырудың мү мкін математикалық моделдерінің бірі дискретті немесе ү здіксіз кездейсоқ ө лшем болып табылады.
Бірақ та, тә жірибе жү зінде, дерек кө здерінің бір ғ ана жағ дайы қ ызық тырмайды, ұ зақ уақ ытта жү зеге асқ ан, дискретті немесе ү здіксіз жү йелі жағ дай, мысалы, телеграммалар, видеосюжеттер жә не т. б Мұ ндай хабарламаларды жазу ү шін дискретті жә не ү здіксіз кездейсоқ ү рдістегі математикалық моделдер қ олданылады.
Моделді қ ұ ру ү шін алдымен l ө лшемді алфавит белгілерін ( 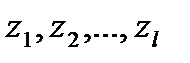 ) білу керек, Бұ дан біз хабарлама қ ұ ра аламыз, мү мкіндігінше бір-бірімен байланыста болу ү шін бө лек белгілер қ ұ ру керек.
) білу керек, Бұ дан біз хабарлама қ ұ ра аламыз, мү мкіндігінше бір-бірімен байланыста болу ү шін бө лек белгілер қ ұ ру керек.
Шеннон ақ паратты теориясының негізгі жағ дайын дә лелдеу кезінде, хабарламаның эродикалық хабарлама дерек кө зі моделі қ олданылды. Математикалық тү рде қ ұ рылғ ан хабарлама эродикалық кездейсоқ жү йелілік тү рінде деп болжалынады. Мұ ндай жү йелілік стационар жә не эродикалық шартты қ анағ аттандырады. Бірінші, бө лек белгінің мү мкіндігі жә не олардың ү йлесімі, хабарлама ұ зындығ ының соң ында орналасуына тә уелсіз екендігін айтады. Екіншіден, статикалық заң дылық, бірлікке жақ ын, бір ұ зын хабарлама зерттеу кезінде алынғ ан, қ ұ рылғ ан дерек кө здерінен барлы, ына тиісті екені келіп шығ ады. Статистикалық сипаттамадан бізді тап осы жағ дайда есептегі бір белгі жү йелілік белгісіздігі қ ызық тырады.
Стационарлы хабарлама кө зі, яғ ни ә рбір белгілерді таң дағ ан кезде ретімен бір біріне байланыссыз таң дайды, оны эрготикалық деп атайды. Оны сонымен қ оса жадсыз қ ор деп те атайды.
Практикада, жиі қ олданылатыны бір хабарламағ а қ олданылатын белгілер осы уақ ытқ а дейін таң далғ ан белгілерге байланысты(жадты қ ор). Ереже бойынша мұ ндай байланыс, алдың ғ ы белгілгілерге байланысты шектелген аймақ та таралады, қ ордың жұ мысын сипаттау ү шін, мақ сатты тү рде Марковтын тізбегін қ олдану керек.
Марков тізбегі n ретті оқ иғ аны сипаттайды, қ андай n оқ иғ аның берілген мә нге қ аншалық та сә йкес келетіндігін. Бұ л n нақ ты оқ иғ алар келесі белгіні беретін кездегі қ ордың жағ дайын сипаттайды. l белгінің R санындағ ы алфавит кө леміндегң қ орды 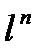 асырмау керек. Жағ дайларды
асырмау керек. Жағ дайларды 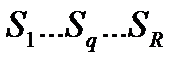
деп, жағ дайды таң дау ық тималдылығ ы 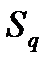
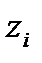 -арқ ылы
-арқ ылы 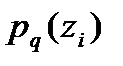 .
. 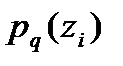 ық тималдылық ты анық тағ анда біз қ ор келесі белгіні берген кезде, оғ ан дейінгі белгілер белгілі екенін жә не қ ордың жағ дайы қ андай екенін болжап білеміз.
ық тималдылық ты анық тағ анда біз қ ор келесі белгіні берген кезде, оғ ан дейінгі белгілер белгілі екенін жә не қ ордың жағ дайы қ андай екенін болжап білеміз.
Егер қ ор 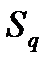 жағ дайында болса, оның жеке энтропиясы H(
жағ дайында болса, оның жеке энтропиясы H( 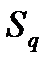 ) келесі қ атынаспен анық талады:
) келесі қ атынаспен анық талады:
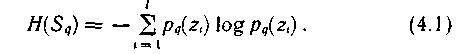
H( 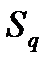 ) барлық жағ дайды пайдалана отырып кездейсоқ шамадан q =
) барлық жағ дайды пайдалана отырып кездейсоқ шамадан q = 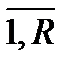 , хабарлама кө зінің энтропиясын табамыз:
, хабарлама кө зінің энтропиясын табамыз:
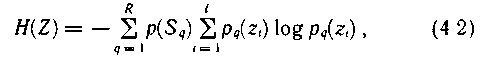
p( 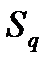 )-
)- 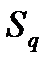 хабарлама кө зінің болатын жағ дай мү мкіндігі.
хабарлама кө зінің болатын жағ дай мү мкіндігі.
H(Z)-анық талмағ андық ты білдіреді.
Хабарлама кө зінің энтропиясын бірнеше жеке жағ дайлар ү шін қ арастырамыз
Егер жалпы белгілер статистикалық байланыс арасында жойылса, 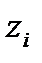 белгісі таң далғ аннан кейін, оның байланысы ө згермейді (R = 1). Сондақ тан, p(
белгісі таң далғ аннан кейін, оның байланысы ө згермейді (R = 1). Сондақ тан, p( 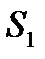 )= 1, жә не де энтропияның негізгі формуласы беріледі:
)= 1, жә не де энтропияның негізгі формуласы беріледі:
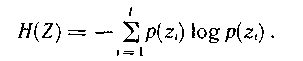
Егер корреляциондық байланыс тек қ ана екі белгінің арасын тексерсе( Марковтің қ арапайым тізбегі), максимальді ә р тү рлі сандардың кү йі, кең ейтілген алфавиттің кө здеріне тең. Сонымен, , R= lи 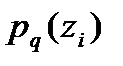 =
= 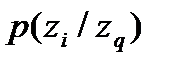 , сол жердегі q =
, сол жердегі q = 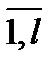 . (4. 2) формуладан келесідей тү рге келтіріледі
. (4. 2) формуладан келесідей тү рге келтіріледі
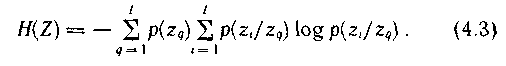
Корреляционды байланыстың қ олданысы, ү ш белгі кө здерінің анық тауышы екі белгінің қ атысуымен ө рнектеледі. Сондық тан да, кө здердің ө ндіріснегі кү йі 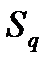 , ың гайлы екі индексті білдіреді
, ың гайлы екі индексті білдіреді 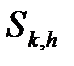 , k=
, k= 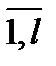 жә не h=
жә не h= 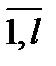 .
.
Онда,
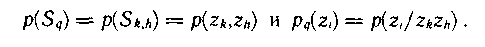
Осы белгіні қ оссақ (4. 2), Келесідей ө рнекті аламыз

Корреляциондық байланыстың белгілер арасында, созың қ ы энтропия кө здері аналогын анық тайды.
Мысалы 4. 1 Эргодикалық стоционарлық дискретті кө здің байланысы, 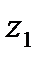
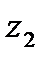
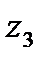 жә не
жә не 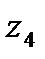 алфавиттік 4 белгі бойынша тұ рады, ық тималды мақ сатты бір белгімен тандап[
алфавиттік 4 белгі бойынша тұ рады, ық тималды мақ сатты бір белгімен тандап[ 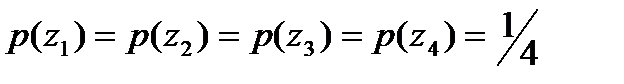 ], мү мкін мә ндерін
], мү мкін мә ндерін 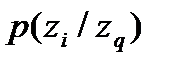 кестеде кө рсетілген бойынша табамыз 4. 1
кестеде кө рсетілген бойынша табамыз 4. 1
Кесте 4. 1.
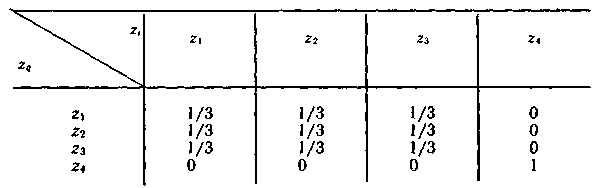
Екі тү рлі жұ мыс режимін қ абылдайтынын 4. 1 кестесінде кө рсетілген. Бұ л мү мкінділік, ¾ тең дікпен, бірінші болып екі тең діктің біреуі таң далады 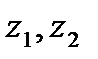 немесе
немесе 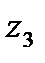 жә не бастаушы кезекпен тең мү мкін белгінің шығ уын форматтуды бастайды. Егер бірінші белгі
жә не бастаушы кезекпен тең мү мкін белгінің шығ уын форматтуды бастайды. Егер бірінші белгі 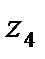 болса(мү мкін шешімі
болса(мү мкін шешімі 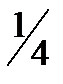 ), онда сақ талғ ан тек
), онда сақ талғ ан тек 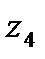 белгісінің кезегі тү рлендіреді.
белгісінің кезегі тү рлендіреді.
Орташа ансамбль бойынша қ олдағ ы кө пшілік бір типті бастаушылар болжамдайды, былайша тө рттен бір бө лігі бірінші бө лімде жұ мыс істейді, ал қ алғ андары екінші режимде. Энтропия бастаушысы (4. 3) сә йкес келеді:
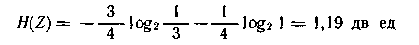
Орташа кезекпен (уақ ыт) қ олданылатын дә л кезектер есептелінеді жә не сондық тан да бастушы функционалдау режиміне тә уелді. Бірінші режимде анық талмағ андық, бір белгіге ұ зын кезекпен(энторпия қ атарымен), 1, 586 дв. ед. тең, ал екіншісінде 0 тең.
Энтропиялар қ анша форматтау кезегімен бастаушы энтропияғ а сә йкес келмейді, жә не ол эргодикалық болмайды.
Кез келген стационарлы бастаушы мә ліметтер бірнеше эгродикалық бастаушылардың қ ұ рамы кө рсетілуі мү мкін, жұ мыс режимдерінен ө згешеленеді.
Эгродикалық белгілердің кезегі. Кезекті мінезі, шынайы бастаушы мә ліметті форматтайды, таң далғ ан шектеулердің болуына тә уелді. Олар былайша орындалады, ә ртү рлі белгілердің мү мкіншілігі жә не олардың арасында корреляционды байланыс болады. Олардың шектеулерінің мү мкіндіктерінің ә ртү рлі форматтаушысы бар.
Мысалы, жадсыз эргодикалық дерекнама тізбектей мына белгілерді шығ арсын 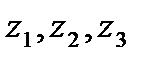 , ал олардың ық тималдығ ы сә йкесінше 0, 1; 0, 3; 0, 6 тең. Бұ дан, ол жасағ ан ұ зын белгілер тізбегінде біз орташа есептегенде бір
, ал олардың ық тималдығ ы сә йкесінше 0, 1; 0, 3; 0, 6 тең. Бұ дан, ол жасағ ан ұ зын белгілер тізбегінде біз орташа есептегенде бір 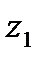 белгісін, ү ш
белгісін, ү ш 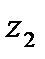 белгісін жә не
белгісін жә не 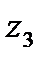 бедгісін кездестіре аламыз. Алайда, егер белгі саны шектеулі болса, тізбектің қ ұ рамы мынадай болатыны ық тимал:
бедгісін кездестіре аламыз. Алайда, егер белгі саны шектеулі болса, тізбектің қ ұ рамы мынадай болатыны ық тимал:
Тек 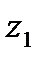 белгісі(немесе
белгісі(немесе 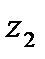 , немесе
, немесе 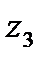 );
);
Тек 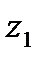 белгісі жә не бір
белгісі жә не бір 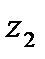 белгісі немесе
белгісі немесе 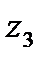 ;
;
Тек 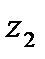 белгісі жә не бір
белгісі жә не бір 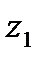 белгісі немесе
белгісі немесе 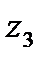 ;
;
Тек 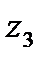 белгісі жә не бір
белгісі жә не бір 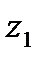 белгісі немесе
белгісі немесе 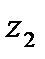 ;
;
Тек 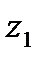 белгісі жә не екі
белгісі жә не екі 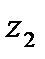 белгісі немесе
белгісі немесе 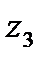 жә не т. с. с.
жә не т. с. с.
Белгі саны артқ ан сайын мұ ндай тізбектің пайда болу ық тималдығ ы азаяды.
Эргодикалық мә лімет кө зі қ ұ рғ ан белгілер тізбегінің негізгі касиетін келесі теорама анық тайды: екі δ > 0 жә не μ > 0 сан каншалық ты кіші болса да, Ν нің жеткілікті дә режеде ү лкен болса, барлық тізбектерді екі топқ а бө луге болады.
Бір топты басқ а кө п топты басып тастайтын топтар қ ұ райды, оның ә р бірінің ық тималдығ ы соншалық ты кіші тіпті олардың ық тималдық тарының қ осындысы ө те аз жә не Nнің жеткілікті дә режеде ү лкен болсада, δ кіші саннан канша болсада кіші болады. Бұ ндай тізбектерді ә деттегі емес деп атайды.
Екінші топ ә деттегі реттілікпен жү реді, ү лкен N олардың пайда болу ық тималдық тарымен бірдей, мұ ндай реттіліктің ρ ық тималдылығ ы келесі тең сіздікті қ анағ аттандырады
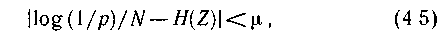
мұ ндағ ы Η (Ζ ) — хабарламалар кө зінің энтропиясы
(4. 5) қ атынасын ұ зақ реттіліктің асимптотикалық тең деудің сипаттамасы деп алуғ а болады. Оларды ары қ арай зерттейміз.
N→ ∞ болғ анда хабарлама кө зі ық тималдылығ ы 1ге жақ ын болып келетін, 1/р тең деуін реттіліктің санын ескере отырып, ә деттегі реттілікті береді. Мұ ндай реттіліктің ық тималдылығ ын ескере келе, оның пайда болуының анық талмағ андығ ы log(l/p) береді. log(l/p)/N ө лшемі анық талмағ андық тудырады. Ә рине, бұ л ө лшем практикалық тү рде энтропия кө зінен ерекшеленбеуі керек, (4. 5) қ атынасын жү зеге асыру керек.
Жадысыз эргодиялық дерек кө здің қ арапайым жағ дайына арналғ ан теореманың дә лелімен шектелеміз. Ол ү лкен сандар заң ынан шығ ады. Ұ зын тізбекте алфавиттің l ( 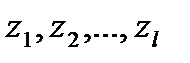 )
) 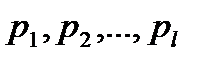 шығ у ық тималдығ ы бар Np
шығ у ық тималдығ ы бар Np 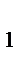 тұ ратын
тұ ратын 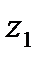 элементтер, Np
элементтер, Np 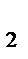 тұ ратын
тұ ратын 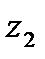 элементтер жә не т. б. N элементіне сә йкес.
элементтер жә не т. б. N элементіне сә йкес.
Онда ρ реализациясының кез келген осығ ан ұ қ сас тізбегіндегі ық тималдығ ы мына ө лшемге сә йкес болады:
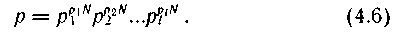
(4. 6) ө рнектің оң жә не сол жақ тарын логарифмдесек, онда аламыз:
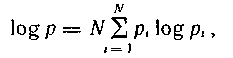
осыдан ( Ν ең ү лкен мә ндерінде)
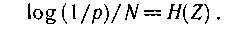
Жалпы жағ дай ү шін теорема марков тізбегін пайдалану арқ ылы дә лелденеді.
lкө зінің алфавитінің кө лемінде жә не тізбектің белгідерінің саны N санының барлық мү мкін тізбегі
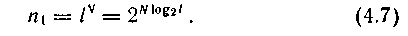
(4. 5) қ атынасты ескере отырып, n 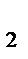 ұ қ сас тізбектерінің санын мына тү рде жазуғ а болады:
ұ қ сас тізбектерінің санын мына тү рде жазуғ а болады:

Онда
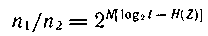
себебі
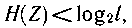
не

Тең сіздік N ү лкейшен сайын кү шейеді.
К. Шеннон ұ зын тізбектердің қ арастырылғ ан қ асиеті ақ паратты эффективті кодтауғ а негіз бола алатынын кө рсетті.
Мысал 4. 2. Мү мкін тізбектің жалпы санының қ андай бө лігін практикалық есептеулерде ескеру керек екендігін бағ алау, егер эргодиялық кө здерінің сипатамасының параметрлері l = 16, Η (Ζ ) = 3, 5 дв. ед, N = 50 тең болса.
(4. 7) жә не (4. 8) сә йкесаламыз
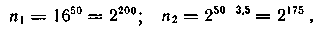
мұ ндағ ы
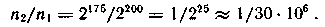
Осығ ан сә йкес ұ қ сас тізбектерге барлық мү мкін реализацияларының ішінде жалғ ыз ғ ана он ү ш миллиондық бө лігі ғ ана келеді.
Артық тық. Ә р тү рлі белгілерді таң дау ық тималдығ ы жә не олардың сә йкестігі туралы белгілі априорлы ақ парат источникпен таң далғ ан белгінің орташа анық талмағ андығ ына алып келеді, сә йкесінше онымен тасымалданатын ақ парат санының да. Тең ық тималды жә не коррелирланбағ ан таң дауда белгіге сол ақ паратты жү ктемені аз кө лемді алфавитті қ олдану арқ ылы қ амтамасыз етуге болады. Осығ ан байланысты хабарлама кө зінің l алфавит артық тығ ы немесе жай ғ ана источник артық тығ ы туралы айтады.
Артық тық тың белгіленуі D, ол берілген кө зінің қ агшалық ты жақ сы қ олданылатынын кө рсетеді:
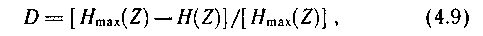
мұ ндағ ы 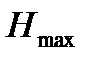 (Z) — максимальдымү мкін энтропия, log l-тең ; H(Ζ ) — источник энтропиясы.
(Z) — максимальдымү мкін энтропия, log l-тең ; H(Ζ ) — источник энтропиясы.
Егер дерек кө зінің артық шылығ ы нольге тең болса, онда қ ұ ралатын хабарлама 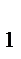 . Сондық тан хаттамалардағ ы белгілердің артық шылығ ын айтады немесе хаттамалар артық шылығ ын, дә л сол D параметр арқ ылы сипаттайды.
. Сондық тан хаттамалардағ ы белгілердің артық шылығ ын айтады немесе хаттамалар артық шылығ ын, дә л сол D параметр арқ ылы сипаттайды.
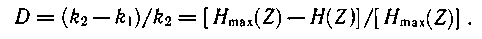
Артық шылық ты хаттама кө зінің кемшілігі ретінде қ арастыруғ а болмайды. Ә детте артық шылық оның физикалық қ асиетінің нә тижесі. Кез-келген тілде болатын шектеулер, еркін ә ріптер жұ бынан тұ ратын, сө здер қ ұ рауғ а кедергі келтіретін, артикуляция ерекшеліктерімен байланысты болады. Артық шылық тың салдары біртекті емес. Бір жағ ынан, артық шлық ты хабарлама жіберіліс кезінде қ осымша жұ мыс талап етеді, мысалы, жіберіліс уақ ытының созылуы т. б. Ал басқ а жағ ынан қ арасақ, априорлы шектеулерге бағ ынатын хабарламаларды қ олдану кезінде, қ ателікті анық тау жә не тү зету мімкіндігі пайда болады, осылар шектеулерді бұ зуғ а алып келеді. Осыдан кейін, артық шылық тың бар болғ аны хабарламаның кедергіге берілмеуіне кө мектеседі. Кө птеген тілдердің жоғ ары артық шылығ ы, адамдар арасындағ ы сенімді қ арым қ атынасты қ амтамасыз етеді. Алайда мә лімет алмасу кезінде, автоматты жү йелерде кә дімгі артық шылық кетіруге жатады. Бұ л былай тү сіндіріледі, заң ды статикалық функциялдану дерек кө зіне базаланатын, қ ателікті анық тау жә не жою алгоритмы, техникалық қ аражаттармен жү зеге асырылуы ө те қ иын. Қ ажеттілік жағ дайында кедергіге тұ рақ тылық ты кө теру ү шін «рационалды»артық шылық енгізіледі, ол техникалық қ ұ ралдардан туатын қ ауіпті жә не маң ызды қ ателіктерді анық тауғ а мү мкіндік береді.
Кедергінің тө мен дең гейінде байланыс каналында кетірулер оптималды болып табылады. Кедергі жоқ болғ ан жағ дайда жә не белгілі бір кө лемдегі мә ліметтерді жіберу ү шін k 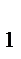 =I/[
=I/[ 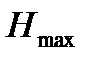 (Z)] I белгі керек. Дә йекті дерек кө зімен қ ұ ралатын, артық шылығ ы бар, максималдыдан аз хабарлама энтропиясы, мә ліметтерді жіберу ү шін I белгілер кө бірек қ ажет болады, нақ тырақ;
(Z)] I белгі керек. Дә йекті дерек кө зімен қ ұ ралатын, артық шылығ ы бар, максималдыдан аз хабарлама энтропиясы, мә ліметтерді жіберу ү шін I белгілер кө бірек қ ажет болады, нақ тырақ; 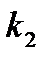 = I/H(Z)
= I/H(Z)
4. 3 мысал Мә тінді орыс тілінде жіберу кезінде артығ ын жоюдан мү мкін болатын эффекті анық тау
Мә тіннің максималды энтропиясы орыс тілінде( е жә не ё, ъ жә не ь ә ріптерін жіберу кезінде айырмашылығ ын елемеу есебінде) орнатылғ ан (3. 3 мысал) жә не ол 5 дв. ед. тең . Онда жеке ә ріптердің пайда болуының ық тималдылығ ының тең емес бө лінуі есебінде энтропиясы анық талғ ан(4. 42 дв. ед). Аралық ық тималдылық ты ескере отырып жә не болжамнан шық сақ, мә тін Марковтың жай тізбегін кө рсетеді, демек энтропия 3. 52 дв. ед тө мендеді деуге болады. Тілдегі барлық шектеулер соның ішінде сө здер арасында энтропия минималды мә нді кө рсетеді 1. 5 дв. ед.
Сонымен орыс тілінің артық тығ ы
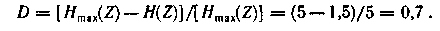
Тілдегі бар шектеу есебінсіз қ ұ рылғ ан байланыс арналарын жә не ә р тү рлі байланыста бола алатын біркелкі ә ріптерді жіберу қ абілетін білдіреді, ақ паратты кедергісіз жіберу барысында орыс тілінде 30 % ғ ана қ олданылады. Артық тылық ты толық тай жою оларды қ олданудың 3 есе тиімділігін жоғ арылатуғ а мү мкіндік береді.
Дискретті хабарламаның ө німділік қ оры. Хабарламаның ө німділік қ оры бірлік уақ ыттағ ы ө ндірту қ орымен информацияның кө лемімен ұ йғ арылады. Бұ л қ ордың сипаттамасын хабарламаны жасау жылдамдығ ы немесе информацияның кіріс ағ ыны деп атайды. Солайша кедергінің хабарлама кө зіне ә сер ық тималдығ ын байланыс арналар моделінің эквивалентті ө згеру сипаттамасын ескеру қ ажет, онда уақ ыт аралығ ында ө тетін хабарлама кө зінің туындауы энтропияғ а тең.
Барлық жағ дайда ә р кү йдің қ ордағ ы беру белгісінің ұ зақ тығ ы ә р тү рлі болуы мү мкін. Беру белгісінің ұ зақ тығ ын 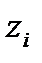 , кү йдегі қ ордың қ алыптасуы S
, кү йдегі қ ордың қ алыптасуы S 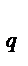 , τ
, τ 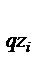 арқ ылы. Онда бір белгінің қ ордағ ы берілуінің орташа ұ зақ тығ ы
арқ ылы. Онда бір белгінің қ ордағ ы берілуінің орташа ұ зақ тығ ы
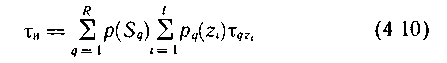
Қ ордың ө німділігін Ī (z) мына формуламен кө рсетуге болады 
(4. 10) дай қ ордың ө німділігінің жоғ арылауы энтропияның артуынан ғ ана емес сонымен қ атар белгінің қ алыптасуының орташа ұ зақ тығ ының тө мендеуінен де болады. Белгінің ұ зақ тығ ы ық тималдылық тың кері пропорцияналдығ ымен алғ ан жө н.
Егер белгінің берілу ұ зақ тығ ы кордың кү йінен тә уелді болмасағ онда барлық белгіге τ бірдей жә не тең, демек τ 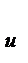 = τ. Ī (Z) тү рі келесідей
= τ. Ī (Z) тү рі келесідей

Бұ л жағ дайда қ ордың ө німділігі максималды энтропияғ а жетеді.
Бақ ылау сұ рақ тары:
1. Дискретті хабарламаның моделді қ оры
2. Белгілерлің эргодикалық реттілік қ асиеттері
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|