2. Дәлдік бағасынын критерисі

⇐ ПредыдущаяСтр 18 из 40Следующая ⇒

2. Дә лдік бағ асынын критерисі

x(t) сигналының мә ні, V(t) туынды функция, сонда 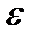(t) дискретизация ағ аттығ ы немесе сә йкес қ алпына келтіру:

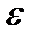(t) = x(t)-V(t)

Ағ аттық бағ асы жеке жә не кө пше сигнал беруде ө ндіріледі.

Кө п жағ дайда туынды функциясының V(t) 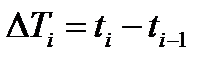интегралында x(t) сигналынан ауытқ уы келесі критериілермен бағ аланады.

1. Кобірек ауытқ у критериі

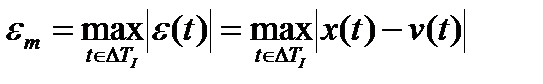
2. Орташа квадратты критериі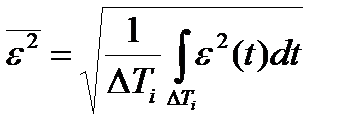

3. V(t) - дан x(t) ауытқ у шарасы тә різді интегралдың критерий келесі тү рде болады: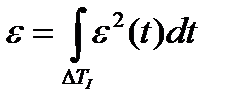

4. Ыктималдық критерисі р{ 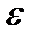(t)( 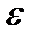_о}=р_оқ атынасыменанық талады.

5. 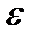_о — ағ аттыктың берілген мә ні;

р₀ -ағ аттық тың 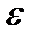_о мә нін асып кетпеу мү мкіндігінің ық тималдығ ы.

3. Базистік функциялар

Дискреттеу есебінің тү сіндірмесі келесідей: [а, Ь] кесіндісінде анық талғ ан, R функциясының класына жататын, берілген x(t) ү шін, [а, Ь] кесіндісінде 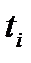бө лігінде нү ктелер саны минимальды немесе 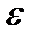(t) 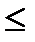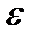_о болатын p(t) функциясын немесе V(t) 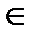S табу керек (мұ ң дағ ы S - функцияның кейбір

тұ рғ ызылғ ан класы), мұ нда 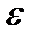_о - ағ аттық тың жіберілген мә ні, 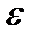(t) - алынғ ан P(t) критериімен жақ ындалғ ан, сә йкес V(t)дан x(t) ауытку бағ асы.

Базистік типін тандаү.

Базистік функциялар типін тандау негізінен дискреттеу қ ұ рылғ ысының қ иындық шектелуінің талап етілуімен жә не сигналды қ алпына келтірумен аныкталады. Алғ ашқ ы сигналды қ алпына келтіру ү шін x(t) таң далуының жиынтығ ы кейбір кө пмү шелерге сә йкес қ ойылады.

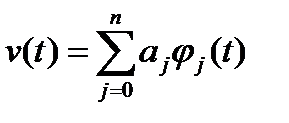
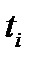есептеу нү ктесіндегі мә н x(t) функциясының мә німен сә йкес келеді.

V(t) туынды функциясы кө біне жақ ындағ ылармен ә эйкес келеді, жалпыжағ дайда олардан ерекшеленуі де мү мкін.

Дискреттеу есебінде қ олданылатын функциялардың негізгі типтері: Фурье қ атары, Котельникова катары, Чебышева полиномы, Лежандра полиномы, дә режелі полиномы, Уолта функциялары, Хаара функциясы, гипергеометриялық.

⇐ Предыдущая 13 14 15 16 171819 20 21 22 Следующая ⇒