
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
3 Кездейсоқ процесстің ықтимал сипаттамалары.
3 Кездейсоқ процесстің ық тимал сипаттамалары.
1. Математикалық кү ту mx(t)=M{X(t)} немесе mx= 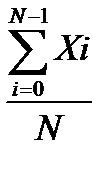
[X(t)- mx(t)] –флуктация деп аталады, яғ ги. δ i= Хi - mx
2. Дисперсия
Dx(t) = M{[X(t) - mx(t)]2} = M{X2(t)} - mx2(t), немесе ( ∑ δ i 2)/15
3. Квадраттық ауытқ ушылық ортасы
____ _______________ ______________
σ х(t)= √ Dx(t) = √ M{[X(t) - mx(t)]2} = √ M{X2(t)} - mx2(t)
4. Стационарлық кездейсоқ процесстің арақ атынастылық функциясы.
Rx (τ )= M{[X(t) - mx(t)]*[X(t+τ ) - mx(t)]}, Rx (0)= Dx
5. Арақ атынастылық коэффициенті 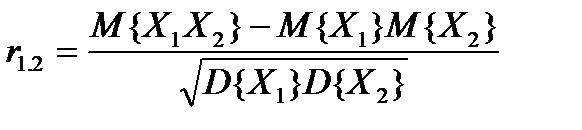
Екі процесс Х1жә неХ2арасында байланыс ө лшемін анық тайды
Арақ атынастылық коэффициентінің мә ні 0 ден 1 дейін ө згереді. Егер r = 0 онда байланыс жоқ, егер r =1 онда екі кездейсоқ процесс арасындағ ы Х1 и Х2 байланыс ө те жоғ ары – сызық тық тә уелділік.
4 Кездейсоқ ө лшемдердің біркелкі ү лестіру.
Біркелкі ү лестіру кезінде ық тимал тығ ыздығ ы Р(х) белгілі бір интервалда тұ рақ ты болады [a, b]
Р(х)
х
Х а в
Математикалық, Р(х)= 1/(b-a), a< x< b
 0, х< a, x> b
0, х< a, x> b
[a, b] ү шін ү лестіру функциясы:
F(x)
х
0 а b
0, x< a
F(x)= (x-a)/(b-a), a< x< b
1, x> b
Бұ л жағ дайда математикалық кү тілім интервалдың мү мкін болатын мә нінің ортасына тең:
Mx= 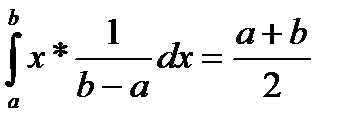 ;
;
σ x(t)= 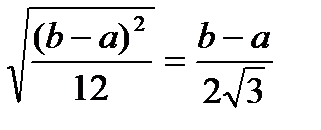
5 Кездейсоқ биіктіктерді дұ рыс анық тау
Сонымен қ атар Гаусстық анық тау деп атайды, анализге ың ғ айлы, практикада жиі кездеседі, соның ішінде байланыс каналдарындағ ы кедергілерді талдау кезінде.
Бұ л заң бойынша тығ ыздық Р(х):
Р(х)=1/( σ x 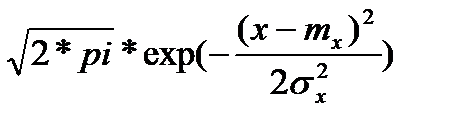 )
)
Тығ ыздық графигі Р(х)
mx=0 и σ x=1 болғ анда
Егерσ x ө згерсе, онда қ исық тың ө зі де ө згереді ( ОУ осімен ұ зарады)
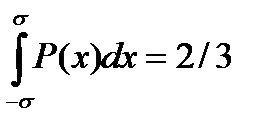 - болжам, кездейсоқ биіктік
- болжам, кездейсоқ биіктік 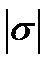 шекарасынан аспайды, шамамен 2/3 қ ұ райды.
шекарасынан аспайды, шамамен 2/3 қ ұ райды.
Қ айта ө ң деуге ұ шырайтын кез келген сигнал уақ ыт пен жиілігі бойынша ө згеретін кездейсоқ сигнал бола алады.
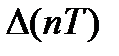 - бө гет
- бө гет
X(nT)
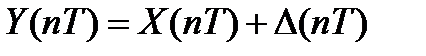
Мінездемелер:
1) Математикалық кү тілім.
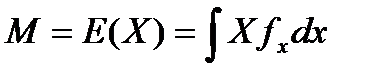 мұ ндағ ы Е(Х)- Х-тің кездейсоқ биіктігінің математикалық ортасы
мұ ндағ ы Е(Х)- Х-тің кездейсоқ биіктігінің математикалық ортасы
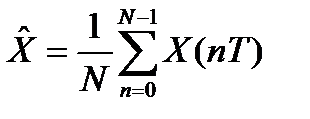
Х(nТ)
N-1 N
2) Дисперсия.
Сигналдың дисперсиясы ү зіліссіз кездейсоқ биіктік ү шін былай анық талады:
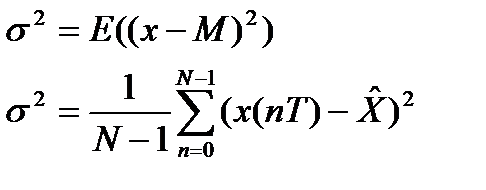
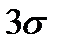 0
0 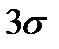
95%
3) Авто корреляция.
Корреляция дегеніміз – Жү йенің қ азіргі қ алпымен алдың ғ ы қ алпы арасындағ ы байланыс.
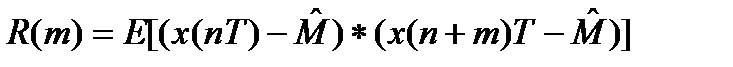
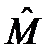 - Орташа мә н немесе математикалық кү тілім
- Орташа мә н немесе математикалық кү тілім
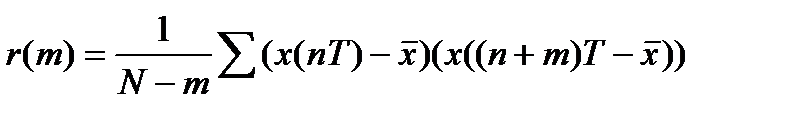

Авто корреляциялық функция кездейсоқ тізбектелудің байланыс мө лшері болып табылады. Егер r(m)=0 болса, онда кездейсоқ тізбектелілер арасында байланыс жоқ.
4) Спектрлік тығ ыздық немесе стационарлық кездейсоқ тізбектелудің қ уаты.
Сигналдың спектрлік тығ ыздығ ы дегеніміз тізбектелідің орташа қ уаты, ол жеткілікті тар жиілік сызығ ынан ө теді.
Бұ л функция Фурье тү рлендіруімен байланысты жә не де келесі тү рде жазылады: 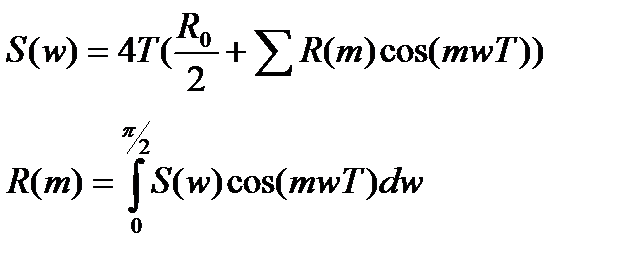
Кез келген ө ң деуге тү сетін сигнал белгілі бір дә режеде уақ ыт жә не жиілік бойынша ө згеретін кездейсоқ сигнал болып табылады. Егер тізбектелудің ә рбір элементі кездейсоқ болатын болса, онда тізбектелу X(nT) кездейсоқ болып табылады.
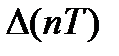 - бө гет
- бө гет
X(nT) Y(nT) 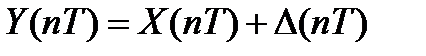
Сипаттамалары:
1) Математикалық кү тілім.
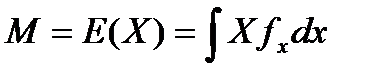
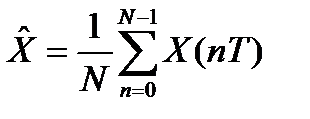
Х(nТ)
N-1 N
2) Дисперсия.
Ү зіксіз кездейсоқ кө лемдегі сигналдың дисперсиясы тө мендегідей:
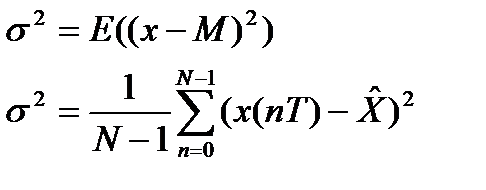
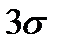 0
0 
95%
3) Авто корреляция.
Корреляция – қ азіргі жә не ә уелгі кү йінің арасындағ ы байланыс. 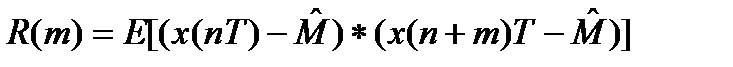
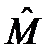 - орташа мә ні немес математикалық кү ту.
- орташа мә ні немес математикалық кү ту. 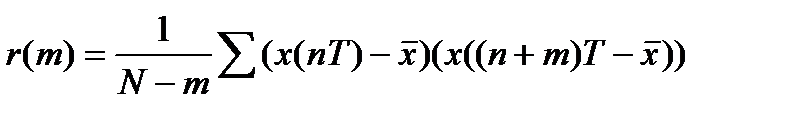

Авто корреляциялық функция кездейсоқ реттіліктер арасындағ ы байланыс шамасы болып табылады. Егер r(m)=0 болса, онда кездейсоқ реттіліктер арасындағ ы ешқ андай байланыс жоқ.
4) Спектральды тығ ыздық немесе стационарлы кездейсоқ реттілік қ уаты.
Сигналдың спектральды тығ ыздығ ы - жеткілікті жің ішке жолақ қ а келетін реттіліктің орташа қ уаты.
Бұ л функция Фурье тү рлендіруімен байланысты жә не келесі тү рде болады:
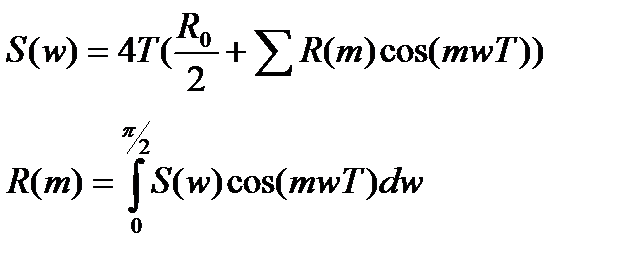
Бақ ылау сұ рақ тары:
1. Кездейсоқ сигналдар ұ ғ ымы жә не олардың ансамблі.
2. Кездейсоқ процесстердің модельдері қ алай қ ұ рылады?
3. Кездейсоқ шамалардың біркелкі таратылуы
4. Кездейсоқ процесстің ық тималдық сипаттамалары қ андай?
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|