1.Сигнал ұғымы және модельдері

4-тақ ырып. Сигнал тү сінігі жә не оның модельдері. Детерминделген сигналдардың кө рсетілу формалары: уақ ыттық, жиіліктік, векторлық.

Дә ріс мақ саты:

1. Сигнал ұ ғ ымы жә не модельдері

2. Детерминделген сигналдардың кө рсетілу формалары

3. Сигналдың уақ ыттық формасы

Сұ рақ тар:

1. Детерминді сигнал туралы нені тү сінеміз?

2. Детерминді сигналдың математикалық кө рсетілім формасының ә ртү рлілігі

3. Функция жү йесінің ортогональды жә не ортонорминальды шарттын жазың ыз.

4. Детерминді сингалдың модельдерін зерттеу не ү шін қ ажет?

5. Сингалдың уақ ыттық кө рсетілімін сипаттаң ыз.

1. Сигнал ұ ғ ымы жә не модельдері

Сигнал – ақ параттық жү йеде арнайы хабарлама жіберілімі ү шін қ ұ рылғ ан ақ параттың материалды тасушы.

Ақ парат тасушы тербеліспен қ олданылады.

Детерминді сигналдар уақ ыттың кез келген мезетінде анық талғ ан. Кездейсоқ тербелісте мә нін анық тау мү мкін болмайтын параметрлер болуы мү мкін. Сигнал ө зімен бірге кездейсоқ тербелісті ұ сынады.

Бірақ детерминді сигналдар моделін зерттеу қ ажет:

1 )Яғ ни детерминді функция жинағ ынжа кездейсоқ процесс болуы мү мкін.

2)Детерминді сигеалдар ақ параттық техника обьектілері ү шін оларды ө лшеу, жө ндеу, реттеу мақ сатында арнайы қ ұ рылғ ан.

2. Детерминделген сигналдардың кө рсетілу формалары

Детерминді сигнал ұ сынылуы мү мкін:

a)Тоқ таусыз аргументтің тоқ таусыз функциясында, Сурет 1.

u(t)!

! ____________________________t.

Сурет. 1

б)дискретті аргументтің тоқ таусыз фуекциясында, Сурет 2

u(t)!

! ½

! ½ ½ ½

! _½ ½ __½ ________½. ½ ½ lllt.

! ½ ½ ½ ½

! ½

Сурет. 2

в) тоқ таусыз аргументтің дискретті фуекциясында, сурет3

u(t)!................................................

!.................................................

! __________________________ t

!......................................................

!.....................................................

!....................................................

Сурет. 3

г) дикретті аргументтің дискретті функциясында, сурет 4

u(t)!..............................................

!...............................................

!................................................

! __________________________. t

!..................................................

!...................................................

4-сурет

Мақ сатымыз: реалды сигналдардың байланыс жү йесі арқ ылы туындайтын зерттеу тапсырмасын оң айлататын сигналды табу.

u(t) сигналының сипаттамасы Дирихле шартын қ анағ аттандырады делік (реалды сигналдар ү шін бұ л шарт кө біне орындалады)

u(t) сигналын 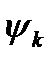_(t) базисты функциясының тұ рақ ты суммасы ретінде алайық:

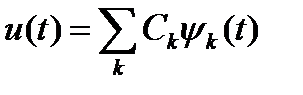(5, 1)

Егер де базисты функия ретінде ортогональды функция алатын болсақ :

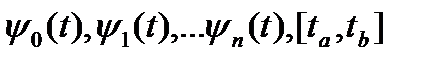киығ ында, барлығ ы ү шін 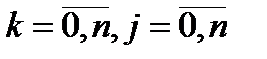, к = j дан басқ а, ол мынағ ан ие:

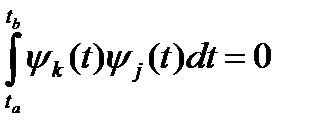(5. 2)

Бұ л система функиясы ортонормардалғ ан болады, егер барлығ ы ү шін 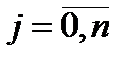болса келесі тең деу:

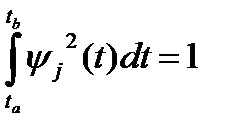(5. 3)

u(t) сигналын ортонормалданғ ан (5, 1) функция ретінде алып С_ккоэффицентін табамыз. (5, 1) тең деуінің оң жә не сол жағ ын 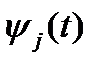ге кобейтеміз жә не [ 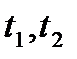] инервалында интегралдаймыз, мұ ндағ ы [ ] [ ]

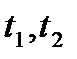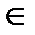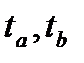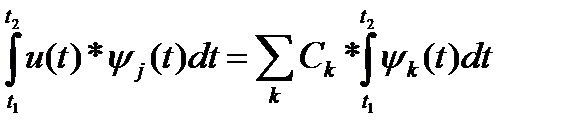(5, 4)

(5. 2) нің туралығ ына байланысты (5. 4) тең деуінің оң жағ ындағ ы барлық интегралдар к 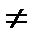j болғ анда нольге тең болады. к=j болса интеграл 1 ге тең

С_k= ò u(t)Y_t(t)dt.

Сигнал сипатының уақ ытша формасы

Сигналдың уақ ытша сипаттамасы дегеніміз U(t) сигналының тарауын айтамыз. Мұ нда базисті функция ретінде бірлік ипульсті функия – дельта-функия қ олданылады:

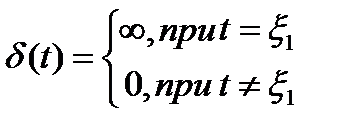
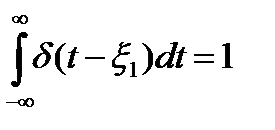
Дельта-функцияның символды орналасуы келесі суретте кө рсетілген

d(t- x₁) :

½ :

½ ½

½ ½ t

0 x

5-сурет

Реалды сиганлды сипаттайтын жалғ ыз ғ ана параметр болып оның қ озғ алыс уақ ыты болып табылады. d функциясы кө мегімен реалды сигналды жазуғ а болады:

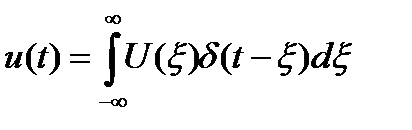(5. 5)

u(t) функциясы бір-біріне жалғ асып жатқ ан шексіз аз ұ зақ тылыұ ты импульс тү рінде сипатталғ ан. 5-і формула сызыкты жү йелер теориясында ерекше орын алады, себебі дельта функция тү ріндегі элементарлы кіріс сигналына жү йенің ә серін орната отырып, орындарын ауыстырғ ан дельта импульстердің шексіз тізбегіне ә серлердің суперпозициясы тү ріндегі еркін кіріс сигналына жү йенің ә серін анық тауғ а болады.

еркін кіріс сигналына жү йе реакциясын кіріс сигналдарының мә ндеріне тең «ауданды» ығ ысқ ан дельта-импульстердің шексіз кезектестігіне реакцияларының суперпозициясы ретінде анық тауғ а болады.

Негізгі ә дебиет: 2[18-24]; 6[43-47];

Қ осымша ә дебиет: 13(20-23]; 161147-157].

Бақ ылау сұ рақ тары:

1. Детерминирленген сигнал дегеніміз не?

2. Детерминирленген сигналдардың математикалық ұ сынылу тү рлері.

3. Функция жү йесінің ортонормаланғ андық жә не ортогональдік шарттарын жазың ыз.

4. Детеминирленген сигнал модельдерін білу не ү шін қ ажет?

5. Сигналдарды кө рсетудің уақ ыттық қ алыбын сипаттаң ыз.

Тақ ырып 5. Кездейсоқ сигналдар. Кездейсоқ процесстер моделдері. Кездейсоқ процестің ық тималдық сипаттамалары.

Лекция мақ саты:

1. Кездейсоқ сигналдар. Іске асыру ансамблі.

2. Кездейсоқ процесстер моделдері.

3. Кездейсоқ шамаларды бірқ алыпты тарату

4. Кездейсоқ шамаларды қ алыпты тарату

5. Кездейсоқ процестің ық тималдық сипаттамалары.

Сұ рақ тар:

1. Кездейсоқ сигналдар тү сінігі жә не оларды іске асыру ансамблі

2. Кездейсоқ моделдер ансамбльдері қ алай қ ұ рылады?

3. Кездейсоқ шамаларды бірқ алыпты тарату

4. Кездейсоқ процестің ық тималдық сипаттамалары қ андай?

1 Кездейсоқ сигналдар

Біз қ алыбын дә л білетін детерминирленген сигналдарғ а қ арағ анда, кездейсоқ сигналдардың лездік мә ндері алдын-ала белгісіз, тек қ андай да бір бірден аз ық тималдық пен болжануы мү мкін. Мұ ндай сигналдар сипаттамалары статикалық , яғ ни ық тималды тү рде болып табылады.

Радиотехникада ық тималдық сипаттаманы қ ажет ететін екі негізгі сигналдар класы бар. Біріншісі бұ л шуылдар – ә ртү рлі физикалық жү йелерде заряд тасымалдаушыларының ретсіз қ озғ алысы себепті туындайтын, уақ ыт бойынша хаостық ө згеретін электромагниттік тербелістер. Екіншіден, кездейсоқ сигналдар болып ақ парат таситын барлық сигналдар табылады, сондық тан байыпты хаттамаларғ а тә н заң дылық тарды сипаттау ү шін де ық тимал моделдерге жү гінеді.

Іске асыру ансамблі

Уақ ыт бойынша ө згеретін кездейсоқ сигналдық математикалық моделі кездейсоқ процесс деп аталады. Анық тама бойынша Х(t) кездейсоқ процесі – бұ л ол кез-келген t уақ ыт мезетінде қ абылдайтын мә ндер кездейсоқ шама болып табылуымен сипатталатын кездейсоқ тү рдегі функция.

Тіркеуге дейін (қ абылдауғ а дейін) кездейсоқ сигналды ортақ статикалық заң дылық тарғ а жү гінетін x_i(t)уақ ыт функцияларының жиынтығ ы (ансамблі) ретінде кө рініс беретін кездейсоқ процесс ретінде қ арастырғ ан жө н. Хаттаманы қ абылдағ ан соң толық тай белгілі болғ ан осы функциялардың бірі кездейсоқ процестің іске асырылуы деп аталады. Бұ л іске асыру енді кездейсоқ емес, детерминирленген уақ ыт функциясы. 6. 1 –суретте бірнеше кездейсоқ процесті іске асырудың мысалы келтірілген.

⇐ Предыдущая 9 10 11 12 131415 16 17 18 Следующая ⇒