pm магнитного момента-e электрона и B индукции магнитного поля в магнетике.

За dt элементарное приращение t времени от, например, момента (рис. 7. 34) t₃= 3T/4 времени элементарное приращение центрального dυ угла окружности имеет с учётом (7. 162) следующую величину, которая определяется длиной хорды, т. е. величиной модуля dL элементарного приращения вектора орбитального (7. 158) L механического момента:

dυ = dL/Lsinυ ↔ dυ = p_mBsinυ dt/Lsinυ ↔ dυ /dt = ω _л = p_mB/L, (7. 163) где ω _л- циклическая (1. 19)из раздела 1. 0 " Физические основы механики" частота вращения векторов орбитальных (рис. 7. 34) соответственно (7. 158) L механического и (7. 157)

p _m магнитного моментов вокругвектора B индукциимагнитного поля в магнетике, к которому эти векторы орбитальных соответственно L механического и p _m магнитного моментов направлены под υ углом, называют ларморовой частотой.

Подставляем (7. 157) p_m = evr/2 модуль вектора p_m орбитального магнитного момента

и (7. 158) L = rmv модуль вектора орбитального L механического момента -e электрона в (7. 163) и получим следующее выражение ω _л ларморовой частоты:

ω _л = p_mB/L ↔ ω _л = (evr/2)B/rmv ↔ ω _л = eB/2m, (7. 164) где ω _л ларморова частота не зависит от υ угла, под которым направлены (рис. 7. 34) векторы орбитальных соответственно (7. 158) L механического и (7. 157) p _m магнитного моментов относительно вектора B индукциимагнитного поля в магнетике, не зависит от r радиуса и vмодуля вектора v скорости вращения -e электрона по окружности и, следовательно, при данном значении B модуля вектора B индукциимагнитного поля в магнетике для всех -e электронов, входящих в состав атома и имеющих e, m соответственно элементарный заряд, массу электрона, эта ω _л ларморова частота постоянна.

Вращение вектора (7. 157) p _m орбитального магнитного момента, направленногопод

υ углом относительно вектора B индукциимагнитного поля в магнетике, можно представить

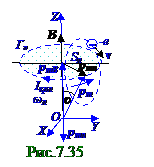
(рис. 7. 35) суммой двух следующих векторов: p _mB - неподвижного инаправленного по вектору

B индукциимагнитного поля в магнетике; p _m_п - подвижного и вращающегося с(7. 164)

ω _л циклической (1. 19)из раздела 1. 0 " Физические основы механики" частотой вращения

" против часовой стрелки" .

Наличиеподвижного и вращающегося вектора p _m_п орбитального магнитного момента можно объяснить дополнительным вращением -e электрона с(7. 164) ларморовой ω _л циклической частотой вращения (рис. 7. 35) " против часовой стрелки" , что эквивалентно протеканию кругового тока" по часовой стрелке" I_крлследующей силы: I_крл = en_л ↔ I_крл = eω _л/2π , (7. 165)где n_л = ω _л/2π - число оборотов в единицу времени или ларморова частота вращения -e электрона " против часовой стрелки" .

Наличие (7. 165) кругового тока" по часовой стрелке" I_крл силы приводит к появлению в диамагнетике вектора p _m_л индуцированного орбитального магнитного момента, вызванного дополнительным вращением -e электронов с(7. 164) ларморовой ω _л циклической частотой вращения (рис. 7. 35) " против часовой стрелки" и поэтому направленного противоположно вектору (7. 77)из раздела 7. 1 " Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях " магнитного p _m момента плоского Г контура с круговым током I_крсилы, который создаёт -e электрон (рис. 7. 18) из раздела 7. 1 " Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях ", вращающийся " по часовой стрелке" по окружности r радиусом с вектором v скорости.

Среднее по t временизначение в диамагнетикепроекции < p_m_л_Z> на OZ ось вектора p_m_л индуцированного орбитального магнитного момента, вызванного дополнительным вращением -e электрона с(7. 164) ларморовой ω _лциклической частотой вращения(рис. 7. 35) " против часовой стрелки" , с учётом (7. 165) индуцированного круговоготока I_крлсилы имеет следующий вид: < p_m_л_Z> = - I_крл π < r_л ²> = - (eω _л/2π )π < r_л ²> = - (eω _л/2)(2/3)r²= = - e(eB/4m)(2/3)r_л²= - e²Br_л²/6m, (7. 166) где π < r_л ²> - cреднее по t времени значение S_лплощади в диамагнетике (7. 77)из раздела 7. 1 " Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях", ограниченной плоскимГ_л контуром

электрическом и магнитном полях ", ограниченной плоским Г_л контуром со cредним по t времени < r_л ²> = (2/3) r_л²квадратом радиуса окружности, по которому протекает индуцированный круговой токI_крлсилы; ω _л = eB/2m - ларморова циклическая (7. 164) частота вращения векторов орбитальных (рис. 7. 35) соответственно (7. 158) L механического и (7. 157) p _m магнитного моментов вокругвектора B индукциимагнитного поля в магнетике, к которому эти векторы орбитальных соответственно L механического и p _m магнитного моментов направлены под υ углом; r_л² - cреднее значениеквадрата радиуса -e электрона (рис. 7. 33), вращающегося по окружности с вектором v скорости вокруг ядра атома.

Среднее по t времени значение в диамагнетике проекции < p_m_л_Z^ат> на OZ ось вектора вектора p _m_л^ат индуцированного орбитального магнитного момента, вызванного дополнительным вращением всех -e электронов Z количеством с(7. 164) ларморовой ω _л циклической частотой вращения

(рис. 7. 35), в атоме диамагнетика имеет с учётом (7. 166) имеет следующий вид:

Z Z

< p_m_л_Z^ат> = ∑ < p_m_л_iZ> = - (e²B/6m)∑ r_л_i², (7. 167)

i = 1 i = 1

где r_л_i² - cреднее значениеквадрата радиуса i -го электрона -e общим Z количеством, вращающихся по окружности с вектором v скорости вокруг ядра в атоме диамагнетика.

⇐ Предыдущая 1 2 3 4 567 8 Следующая ⇒