Хелпикс

Главная

Контакты

Случайная статья



B1nсоставляющейи вектором B1 индукции магнитного поля в среде магнетикаμ1 магнитной проницаемостью, а также  α2 угол  между нормальной B2nсоставляющейи вектором 2 страница

⇐ ПредыдущаяСтр 2 из 8Следующая ⇒


                                                                             [  , [( B/ μ 0) - J ] ] = [   , H] = rotH = [   H] = j .        (7. 121)

 

              Теорема о циркуляции вектора напряжённости магнитного поля в                                             дифференциальном и интегральном видах

 

       Согласно (7. 121) ротор вектора H напряжённости  магнитного поля в произвольной точке пространства, занятого магнетиком, равен вектору j плотности  макроскопического или тока проводимости в этой точке пространства.                                                                                                       

       Выражение (7. 121) является теоремой о циркуляции вектора H напряжённости  магнитного поля по Г контуру, занятого магнетиком, в дифференциальном виде.

       Возьмём в области пространства, занятого магнетиком, в котором существует вектор   

H напряжённости  магнитного поля и вектор j плотности  макроскопического или тока проводимости, произвольный воображаемый Г контур с " натянутой" на него поверхностью                S площадьюи образуем следующее выражение с использованием (7. 121):  

O 
O
                                                                                                                            ∫ [   H] d S = ∫ j d S .        (7. 122)                                                                                                            S       S                            Перейдя в(7. 122) с использованием теоремы Стокса   от   интеграла по поверхности               S площадью, " натянутой" на воображаемый Г контур, к интегралу по этому воображаемому   Г контуру, с учётом (7. 28) из раздела 7. 1 " Магнитостатика " результирующего тока Iрез силой  в магнетике через поверхность  S площадью, охватываемую этим воображаемым Г контуром, а также с учётом вектора j плотности макроскопического или тока проводимости через элементарную поверхность dS площадью этой поверхности S площадью, получим следующее выражение:                                                                                                                ∫ [   H] d S   = ∫ H d l =  ∫ j d S = Iрез.      (7. 123)                                                                                         S              Г    S                               Согласно (7. 123) циркуляция вектора H напряжённости магнитного поля по воображаемому          Г контурув области пространства, занятого магнетиком, равна  результирующему               

Iрез макроскопическому или току проводимости  через поверхность S площадью, которую охватывает этот воображаемый Г контур.                                                                         

O
       Если макроскопические токи I1, I2 … In силой или токи проводимости текут по n проводам, охватываемым воображаемым Г контуром, то (7. 123) приобретает следующий вид:           n

                                                                                                                         ∫ H d l = ∑ Ii.  (7. 124)                                                                                                                   Г      i = 1                  Выражение (7. 124) является теоремой о циркуляции вектора H напряжённости  магнитного поля по воображаемому Г контурув области пространства, занятого магнетиком, в интегральном виде: циркуляция вектора H напряжённости  магнитного поля по воображаемому Г контуру, который охватывает в области пространства, занятого магнетиком,  n проводников с токами I1, I2 … In силой, равняется алгебраической сумме этих токов.                                                         

 

Магнитная восприимчивость и магнитная проницаемость. Диамагнетики,                                                    парамагнетики и ферромагнетики

     

       В вакууме вектор J намагниченности J = 0, поэтому вектор H напряжённости  магнитного поля связан в вакууме согласно (7. 120) с вектором B 0индукции магнитного поля следующим образом:                                                                                                                 H = B 0 / μ 0 .   (7. 125)       Вектор J намагниченности в области пространства, занятого магнетиком, принято связывать не с результирующим вектором B индукции магнитного поля в произвольной точке пространства, занятого магнетиком, а с вектором H напряжённости магнитного поля в этой области пространства. С учётом (7. 120) коллинеарности векторов B, H соответственно индукции,   напряжённости магнитного поля векторы J, H намагниченности,   напряжённости магнитного поля области пространства, занятого магнетиком, связаны друг с другомследующим χ коэффициентом пропорциональности :                                                                                         J = χ H, (7. 126) где χ - магнитная восприимчивость материала магнетика, которая у диамагнетиков отрицательна и мала по абсолютной величине, у парамагнетиков тоже невелика, но положительна, у ферромагнетиков положительна и достигает очень больших значений.                          

       В изотропных веществах вектор J =χ H намагниченности из(7. 126) совпадает по направлению с вектором H напряжённости магнитного поля у парамагнетиков, т. к. магнитная

χ восприимчивость этих парамагнетиков положительна, а у диамагнетиков   вектор

J намагниченности противоположен по направлению вектору H напряжённости магнитного поля, т. к. магнитная χ восприимчивость этих магнетиков отрицательна и мала по абсолютной величине.

       У ферромагнитных материалов, например, у железа, кобальта и их сплавов связь междувектором J намагниченности этих материалов и вектором H напряжённости магнитного поля представляет собой сложную нелинейную зависимость.                     

       Подставим (7. 126) в (7. 120) и получим следующую связь вектора H напряжённости  магнитного поля с результирующим вектором B индукции магнитного поля в произвольной точке пространства, занятого магнетиком:             ( B/ μ 0 - χ H )= H ↔ H = B /μ 0(1 + χ )= B /μ 0μ ,   (7. 127) где μ = (1+χ ) - магнитная проницаемость, которая для однородных магнетиков является постоянной безразмерной величиной, а для неоднородных магнетиков зависитот координат точки пространства, в которой эта μ магнитная проницаемость определяется.         

       Согласно(7. 127) вектор H напряжённости  магнитного поляесть вектор, имеющий то же направление, что и результирующий вектор B индукции магнитного поля в произвольной точке пространства, занятого магнетиком, но в μ 0μ  раз меньший по модулю.

 

    Нормальные составляющие вектора напряжённости и индукции магнитного поля на                                  границе раздела магнетиков

               

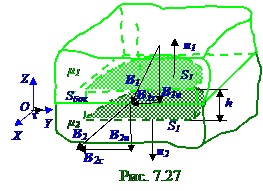
       Согласно теореме (7. 19) из раздела 7. 1 " Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях " Гауссав интегральной форме общий Фmo магнитный поток через замкнутую поверхность S площадью равен нулю. На рис. 7. 27 замкнутая поверхность S площадью представляет собой в среде магнетиков воображаемый полуцилиндр с S1 площадями оснований, прямоугольного сечения в горизонтальной OYZ плоскости и цилиндрической боковой поверхностью Sбок площадью. Результирующие векторы B 1 и B 2 магнитной индукции поляв среде магнетиков с магнитными проницаемостями соответственно μ 1 и μ 2 имеют нормальные составляющие B 1n и B 2n   к верхней и нижней поверхностям воображаемого полуцилиндра с S1 площадями оснований.  

       Вследствие противоположного направления вектора B 1 и положительной n 1нормали   к верхней поверхности S1 площадью, а также вследствие совпадения направления вектора B 2 и положительной n 2нормали   к нижней поверхности S1  площадью, проекции B1n иB2n на соответственно n 1, n 2нормали результирующих векторов B 1 и B 2 магнитной индукции поляв среде магнетиков с магнитными проницаемостями μ 1 и μ 2 имеют противоположные знаки.                                   

       С учётом (рис. 7. 27) малости Sбок площади цилиндрической боковой поверхности по сравнению с S1 площадями оснований воображаемого полуцилиндра общий Фmo магнитный поток через  замкнутую поверхность S площадью этого воображаемого полуцилиндра в среде магнетиков будет состоять только из нормальных составляющих B 1n и B 2nк верхней и нижней поверхностям S1 площадью воображаемого полуцилиндра.

       С учётом теоремы (7. 19) из раздела 7. 1 " Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях "  Гауссав интегральной форме, противоположности знаков упроекций B1n иB2n на соответственно n1, n2 нормали результирующих векторов B 1 и B 2 магнитной индукции поляв среде магнетиков с магнитными проницаемостями      μ 1 и μ 2, а также с учётом равенства верхнего и нижнего оснований S1 площадью воображаемых полуцилиндров общий Фmo магнитный поток через  замкнутую поверхность S площадью этого воображаемого полуцилиндра в среде магнетиков имеет следующий вид:                 Фmo = B2n S1  - B1n S1  = 0 ↔ B1n  = B2n.  (7. 128)

       При определении в(7. 128) общего Фmo магнитного потока через замкнутую поверхность                (S) площадью воображаемого полуцилиндра не учитывались тангенциальные B 1τ   и B 2τ составляющие результирующих векторов B 1 и B 2 магнитной индукции поляв среде магнетиков с магнитными проницаемостями соответственно μ 1 и μ 2, т. к. предполагалась малая h толщина воображаемого полуцилиндра с S1 площадямиоснований, вследствие чего:  h → 0; S2 → 0; Sбок → 0.

       Поэтому магнитный поток через прямоугольное сечение S2 площадьюи цилиндрическую боковую поверхностью Sбок площадью воображаемого полуцилиндра тоже стремится к нулю.               

       Подставим (7. 127) B = μ 0 μ H пропорциональной связи вектора H напряжённости  магнитного поляс результирующим вектором B магнитной индукции поляв среде магнетика с

μ магнитной проницаемостью, котороесправедливо, в частности, для проекций H1n, H2n на соответственно n 1, n 2нормали к верхней и нижней поверхности S1 площади векторов H 1, H 2 напряжённостей  магнитного поля, в выражение (7. 128) и получим следующее соотношение между этими проекциями H1n, H2n на границе раздела магнетика с магнитными проницаемостями соответственно μ 1 и μ 2:

                                                                     μ 0 μ 1H1n =  μ 0 μ 2H2n ↔ H1n/H2n = μ 2/μ 1.       (7. 129)

Таким образом, из (7. 128) и  (7. 129)векторы нормальных составляющих B1n и B2n индукции магнитного поля на границе магнетиковсμ 1 и μ 2магнитными проницаемостямисохраняют своё направлениеи модуль, а векторы нормальных составляющих H1n и H2n напряжённости H магнитного поля сохраняют своё направление, но изменяютвеличинусвоего модуляпропорционально μ 2/ μ 1 отношению магнитных проницаемостей μ 2 и μ 1.                                                                       
                                                                                     

 

    Для случая μ 2 > μ 1 векторы (рис. 7. 28) нормальных составляющих H 1n и H 2n напряжённости

H магнитного поля сохраняют своё направление, но модуль (7. 129)H1n больше H2n в μ 2/μ 1 раз.

 

Тангенциальные составляющие вектора напряжённости и индукции магнитного                                           поля на границе раздела магнетиков

 
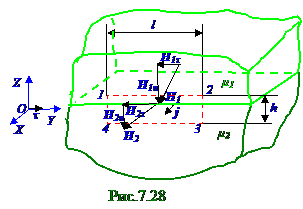
В (рис. 7. 28) пренебрежении h толщиной                              1 - 2 - 3 -4 контура, т. к. h → 0  циркуляция(7. 124) вектора H напряжённостимагнитного поля поэтому 1 - 2 - 3 -4 контуру  в области пространства на границе магнетиковсμ 1 и μ 2 магнитными проницаемостямиприналичии в общем случае вектора  j плотности макроскопическихили токов проводимостина поверхностиграницы раздела магнетиков будет иметь следующий вид:                                                    ∫ Hdl = ∫ H1τ dl + ∫ H2τ dl = jl,                 (7. 130)        1-2 -3-4    1-2   3-4


O

 

где j - модуль вектора j плотности тока, перпендикулярного ограниченной 1 - 2 - 3 -4 контуром     поверхности,  макроскопических или токов проводимости на границе раздела магнетиков; l - длина границы раздела магнетиков, по которой протекают токи проводимости.

O
Циркуляция (7. 130) векторов H 1τ и H 2τ тангенциальных составляющих вектора                           H напряжённости магнитного поля при обходе   1 - 2 - 3 -4 контурапо " часовой стрелке" c учётом отрицательной проекции вектора d l  на направление вектора H 1τ тангенциальной составляющей вектора H напряжённости магнитного поля приобходе 1 - 2  части контура l  длиной, а также с учётом положительной проекции вектора d l  на направление вектора H 2τ тангенциальной составляющей вектора H напряжённости магнитного поля приобходе3 -4 части контура l длиной имеет следующий вид:                                   ∫ H d l =   ∫ H 1τ d l + ∫ H 2τ d l = H2τ l  - H1τ l = jl ↔ H2τ - H1τ = j.  (7. 131)                                                     1-2 -3-4    1-2        3-4

Таким образом согласно (7. 131) выражению векторы H 1τ и H 2τ тангенциальных составляющих напряжённости H магнитного поля на границе раздела магнетиков с магнитными проницаемостями соответственно μ 1 и μ 2 приусловии наличия вектора j плотности макроскопических или токов проводимости на этой поверхностигранице раздела магнетиков сохраняют своё направление, но (рис. 7. 28) изменяют величинусвоего модуля на величину         j модуля вектора j плотности тока проводимости, существующего на поверхностигранице раздела магнетиков и перпендикулярного OYZ плоскости, в которой находятся векторы H напряжённости магнитного поля.

       При отсутствии вектора j плотности макроскопических или токов проводимости на поверхностиграницы раздела магнетиков (7. 131) выражение принимает следующий вид:

                                                                                                  H2τ - H1τ = 0 ↔ H2τ = H1τ .    (7. 132)        Подставим (7. 127) H = B/ μ 0μ пропорциональной связи вектора H напряжённости  магнитного поляс результирующим вектором B магнитной индукции поляв среде магнетика с

μ магнитной проницаемостью, котороесправедливо, в частности, для проекций H1τ , H2τ на направление τ единичного (рис. 7. 28) вектора векторов H 1, H 2 напряжённостей  магнитного поля,  в выражение (7. 100) и получим следующее соотношение между проекциями B1τ , B2τ на направление

τ единичного вектора результирующего вектора B индукции магнитного поля на границе раздела магнетика с магнитными   проницаемостями соответственно μ 1 и μ 2 при условии отсутствия вектора j плотности макроскопических или токов проводимости на этой поверхностигранице раздела магнетиков:                                                                          B1τ /μ 0 μ 1 = B2τ /μ 0 μ 2 ↔ B1τ /B2τ = μ 1/μ 2.        (7. 133)       Таким образом из (7. 132),  (7. 133) векторы H 1τ и H 2τ тангенциальных составляющих вектора             H напряжённости магнитного поля на границе магнетиков с магнитными проницаемостями соответственно μ 1 и μ 2 сохраняют своё направление и модуль, а векторы тангенциальных составляющих вектора B индукции магнитного поля B 1τ и B 2τ сохраняют своё направление, но изменяют величинусвоего модуля пропорционально отношению магнитных проницаемостей μ 1 и μ 2 при условии отсутствия вектора j плотности макроскопических или токов проводимости на этой поверхностиграницы раздела магнетиков.

            Для случая μ 2 > μ 1 векторы (рис. 7. 27) тангенциальных составляющих вектора B индукции магнитного поля B 1τ и B 2τ сохраняют своё направление, но модуль (7. 133)B2τ больше B1τ в μ 2/μ 1 раз.

 
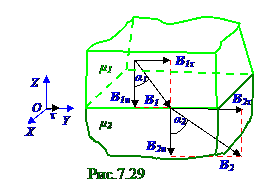
Векторы B индукции (рис. 7. 29) магнитного поля B1, B2 в среде магнетиков с μ 1 и μ 2 магнитными проницаемостямисоответственно имеют согласно (7. 128)равные нормальные составляющие B1n и B2n. Тангенциальныесоставляющиевектора B индукции магнитного поля B1τ , B2τ зависят при отсутствиивектора  j плотности макроскопических или токов проводимостина поверхностигранице раздела магнетиков согласно (7. 133) от величин μ 1 и μ 2магнитных проницаемостей. Поэтому α 1 угол  c учётом (7. 128), (7. 133)между нормальной


                                                                                                                                                                         

B1nсоставляющейи вектором B1 индукции магнитного поля в среде магнетикаμ 1 магнитной проницаемостью, а также  α 2 угол  между нормальной B2nсоставляющейи вектором

B 2 индукциимагнитного поляв среде магнетика с μ 2 магнитной проницаемостью связаны между собой следующим соотношением:                                      tqα 1/tqα 2 = (B1τ /B1n)/(B2τ /B2n)= μ 1/μ 2,   (7. 134)


⇐ Предыдущая12345678Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.